| Issue |
J. Space Weather Space Clim.
Volume 3, 2013
|
|
|---|---|---|
| Article Number | A11 | |
| Number of page(s) | 8 | |
| DOI | https://doi.org/10.1051/swsc/2013033 | |
| Published online | 06 March 2013 | |
Single-frequency GNSS retrieval of vertical total electron content (VTEC) with GPS L1 and Galileo E5 measurements
1
University of the Federal Armed Forces Munich, Faculty of Aerospace Engineering, Department LRT9.2, 85577 Neubiberg, Germany
2
Geodetic Observatory Wettzell, Federal Agency of Cartography and Mapping (BKG), Sackenrieder Str. 25, 93444 Bad Kötzting, Germany
3
University of Ilorin, Physics Department, P.M.B., 1515 Ilorin, Nigeria
4
Alexander von Humboldt Research Fellow at University of the Federal Armed Forces Munich, Germany
* Corresponding author: e-mail: dr_schueler@gmx.net
Received:
27
February
2012
Accepted:
13
February
2013
The European Galileo satellite navigation system offers a signal in space that will enable us to deduce range measurements of unprecedented precision: the E5 broadband signal. These new code range measurements would be up to three or four times more accurate compared to nowadays GPS L1. However, E5 will be the only Galileo signal of that outstanding performance. For this reason, a single-frequency single-site ionospheric delay estimator is experimented with to retrieve absolute VTEC data. A single-frequency VTEC retrieval algorithm was developed and tested. It is following the principles published in Xia (1992), Issler et al. (2004), and Leick (1995, 2004). During the validation phase, we devoted considerable time to process GPS L1 measurements in order to assess the level of precision obtainable with current real-world GNSS measurements. We found the global average RMS to be close to 4 TECU (1.5–2.5 TECU at mid- and higher latitude stations) what is considered to be a promising result. The very limited Galileo satellite constellation present during the time of this study did not allow us to run the absolute VTEC retrieval algorithm with real Galileo data. However, we can demonstrate the significant improvements related to the Galileo E5 signal with the help of satellite-specific ionosphere retrieval results from the Galileo experimental satellite GIOVE-B, although only a limited set of data was available for that purpose. In addition, we are presenting a test case based on simulated data that also underlines that the precision figures will clearly improve when using Galileo E5 data. This could make single-frequency ionosphere retrieval more attractive in the future.
Key words: vertical total electron content (VTEC) / GPS / Galileo / GNSS / E5 wideband signal / ionosphere monitoring
© T. Schüler et al., Published by EDP Sciences 2013
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
One method to separate the ionospheric delay from all the other components inherent in GNSS measurements is to exploit the characteristics of group versus phase delay. In fact, the ionospheric delay has opposite signs on both the code range (“pseudoranges”) and carrier phase measurements.
Although not in widespread use today, a single-frequency GNSS receiver can actually be useful for sensing ionospheric delays, too. A least-squares block adjustment procedure is used for this purpose. A sequential filter implementation of this algorithm, which is not in the focus of this paper, could be used for real-time ionosphere monitoring.
1.1. Importance of code ranges
The single-frequency approach makes use of a linear combination of code range and carrier phase measurements. Code ranges are less accurate than carrier phase measurements, in particular because multipath effects impact ranges to a larger extent than carrier phases, but there are variations for the different GNSS signals depending on design parameters such as signal structure and bandwidth (Eissfeller et al. 2007). In particular, the E5 AltBOC-modulated broadband signal of the future Galileo navigation satellite system will feature an outstanding multipath performance that can be three or even four times lower compared to the current signals such as GPS L1. The increased multipath resistance and reduced code noise are a result of both the AltBOC(15,10) modulation applied to this signal and the enhanced bandwidth of more than 50 MHz compared to 24 MHz of the GPS L1 signal in space. This fact can make the single-frequency approach more competitive compared to dual-frequency methods, although receiver performance has evolved during the past too, so that GPS L1 data can also be successfully processed as demonstrated in this paper.
1.2. Literature review
The idea to use single-frequency GPS measurements for ionospheric delay estimation is not new, but literature on this topic is limited, mainly because of the code noise problem outlined before that has delayed the realization of this concept significantly.
Yuan & Ou (2001) outline the basic methodology, but the authors only recognize the relative character of the code-minus-carrier approach rather than the possibility to determine absolute total electron content.
Coco et al. (1991) published an article focusing on the estimation of differential instrumental delay biases to make the estimation of total electron content from dual-frequency GPS measurements feasible. This comprises, in particular, the estimation of the L2-L1 differential group delay. Although a calibration technique is depicted, the horizontal interpolation approach carried out for the total electron content is similar to the one followed in this note.
Xia (1992) describes an experiment to retrieve absolute ionospheric delay errors from a single-frequency GPS receiver. This approach published in 1992 underlines that the use of a code range minus carrier phase combination (CMC) enables us to determine the total electron content from data collected on just one instead of both GPS frequencies, although some details necessary for a successful delay retrieval are not completely clear, and the author admits that this study is just a very first step and a demonstration of the technique. Just at the same conference, Cohen et al. (1992) present a paper of similar contents. A first-order spherical harmonics model is chosen for horizontal interpolation of the ionospheric delays at the pierce points, which are expressed in a sun-fixed reference frame. A couple of years later, Lestarquit et al. (1996) depict a sequential filter algorithm for L1 only ionospheric delay estimation, which is also mentioned by Issler et al. (2004). Finally, a more recent publication by Mayer et al. (2008) is – in essence – of the same contents.
2. Description of algorithm
As already mentioned, the method of single-frequency site-specific VTEC retrieval is not new, so that only a brief description is given here. The reader may refer to the literature cited in the preceding section. In particular, we refer to Leick (1995, 2004) who outlines this method, although its application is focusing on position accuracy improvement rather than ionosphere monitoring in his textbook.
The appropriate observable containing the ionospheric delay in slant direction is the code-minus-carrier observation that eliminates all geometry-dependent components with the impact of the ionospheric propagation delay being the prominent remainder in the observation equation: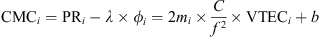
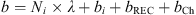 (1)where
(1)where
CMC: Code-minus-carrier observable containing the ionospheric delay (m)
PR: Code range measurement (“pseudo range”) (m)
λ: Carrier wave wavelength (m)
ϕ: Carrier phase measurement (cycles)
m: Mapping function to project slant to zenith direction (/)
C: Constant; C ≈ 40.309 × 1016 according to Petit & Luzum (2010)
f: Carrier wave frequency (Hz)
VTEC: Vertical total electron content (TECU)
bCH: Receiver interchannel bias
Our target parameter is VTEC that is to be estimated from a set of CMC observables to various GNSS satellites. It should be noted that VTECi differs for each satellite i, because the rays are passing through different parts of the ionosphere, and a number of bias terms are to be determined. As a matter of fact, this system of equations cannot be solved ad hoc, because it is underdetermined. A common method to solve this problem is to use a horizontal interpolation function, a low-order polynomial in our case with three to four parameters, and to determine its coefficients rather than each piercepoint-related VTECi individually. The variations in time domain are modeled as piecewise linear function. The system of equations is then solved using a least-squares block adjustment procedure.
2.1. Biases
A bias problem is present and must be addressed. The sum of all biases is denoted as b here. The satellite-receiver-specific ambiguity terms are important bias terms in addition to the satellite-specific bias bi. The ambiguities change as soon as a (non-fixable) cycle slip occurs. Such phase jumps are usually related to obstacles hiding the satellite signal, strong multipath effects and ionospheric scintillations. The receiver-specific bias is considered to be common to all observations. In addition, we take an interchannel bias into consideration: Nowadays receivers use a number of hardware channels for satellite tracking. Each of these channels may exhibit an individual delay. These delays are supposed to be estimated in a geodetic-grade receiver, e.g., by tracking one selected satellite on all hardware channels, but our algorithm is also supposed to work with mass-market receivers which are very cheap and for which we cannot assume that such receiver-internal calibration procedures will be carried out with sufficient accuracy. However, please note that mass-market receivers might be equipped with less stable tracking loops and thus are more susceptible to loss of lock causing more cycle slips than high-quality receivers.
We effectively estimate the complete b terms for each uninterrupted satellite arc (typically between 150 and 180 min using a 20° elevation mask). Our assumption is that the bias term does not change over that (relatively short) period of time. We do not separate the common bias bREC from the rest of the terms in our implementation.
2.2. Mapping function
The slant ionospheric propagation delays are separated from the bias terms with the help of a mapping function that relates the slant delay to the vertical direction. A commonly used approximation called “single-layer model” of the ionosphere is adopted, see e.g., Hoffmann-Wellenhof et al. (1993). The precision of this mapping function is critical from our experience, even when using an elevation cut-off of 20°. For this reason, station-specific effective heights were adopted and a modified mapping function is used that is documented in Dach et al. (2007). We can confirm their global effective ionosphere height of 450 km, but considerable variations can be stated, predominantly in the North-South direction. We are using a fixed height for each site: the median from a daily analysis of annual data sets. Smaller seasonal variations exist for certain stations, diurnal variations can be present but have not been investigated yet. An alternative method using the NeQuick2 ray-tracer (Nava et al. 2008) to derive precise obliquity factors is underway.
3. GPS IGS LEO network test
The year 2003 appears to be a proper time period to test the single-frequency ionosphere monitoring approach with real-world GPS data. Intentionally not right in the middle of the solar cycle’s maximum activity nor located in its minimum, it is still a period of slightly higher activity than what we would call “typical”. Moreover, the already-mentioned October 2003 ionosphere storm (Doherty et al. 2004) provides a prominent signature in the data sets of most stations.
3.1. General information
The IGS LEO network is a sub-network of the IGS tracking network (see http://igscb.jpl.nasa.gov/network/netindex.html, last access: 7 November 2011) implemented in support of LEO satellite missions (e.g., for radio occultation). These stations provide “high-rate” data with a sampling interval of 1 s in data fragments of 15 min. The normal data interval is 30 s which is too coarse for single-frequency ionosphere analysis, mainly because cycle slip detection is not as easy as for dual-frequency GPS data and essentially requires high-frequency data. Cycle slips occur under certain conditions (e.g., strong multipath and obstructions) and change the ambiguity term Ni mentioned in Formula (1).
The available data of more than 40 reference stations shown in Figure 1 were processed using the GPS L1 signal. The results portrayed in this paper are focusing on a profile of nine selected stations which are approximately aligned from the north to the south, see Figure 2.
 |
Fig. 1. Map of the IGS high-rate reference stations used in the 2003 long-term data analysis experiment. |
 |
Fig. 2. Selection of IGS network sites used for all diagrams in this paper; RMS “speedometer” visualization in (TECU) on the left and right. |
The reference data used to compute differences and to derive the corresponding statistical descriptors were interpolated from IGS IONEX grids (combined final product) which are officially marked to be accurate at a level of 2-8 TECU (see http://igscb.jpl.nasa.gov/components/prods.html; last access: 7 November 2011). Although limited in spatial resolution (the grid size is 2.5° N/S × 5.0° E/W), the IONEX maps are derived from dual-frequency GPS data. We assume that these gridded data are suitable to serve as reference data versus our single-frequency results.
GPS data processing was carried out on daily data batches. The variations in ionospheric delay are modeled as piecewise linear functions with a temporal resolution of 30 min. The daily result files are then compared to the IONEX-derived VTEC values so that up to 12 data samples are available for comparison each day (no interpolation of IONEX data in time domain performed to avoid interpolation errors; averaging of four 30 min VTEC estimates from single-frequency algorithm performed for purposes of compatibility). The term “number of samples” designates the number of these 2-h-sample differences di (between IONEX-derived VTEC and single-frequency estimates) actually available for the comparison. The differences are logged to annual output files from which the annual bias, i.e., the “mean” 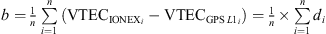 , is computed with n being the number of samples, i being an index, VTECIONEX being the vertical total electron content from the IONEX grid, and VTECGPS L1 that of the single-frequency GPS data processing. The root mean square is
, is computed with n being the number of samples, i being an index, VTECIONEX being the vertical total electron content from the IONEX grid, and VTECGPS L1 that of the single-frequency GPS data processing. The root mean square is 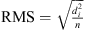 and contains both the intrinsic dispersion of the differences as well as the systematic error, i.e., the annual bias.
and contains both the intrinsic dispersion of the differences as well as the systematic error, i.e., the annual bias.
3.2. Discussion of results
Figure 3 shows diagrams of the biases (“mean”) and RMS values for the nine selected stations portrayed in Figure 2 in a graphically more appealing manner. Note that data outages are present in some of the data sets. The number of samples (differences) available for statistical analysis is between 4100 and 4380 for four out of the nine presented sites. Slightly larger data losses are linked to KIRU, VILL, and MAS1 (between 3090 and 3180 samples), and the largest data outages occurred at MSKU (1453 samples) which was not recording data for the complete year 2003.
 |
Fig. 3. Diagram of VTEC biases and RMS in (TECU) for the GPS L1 results. |
Typically, the RMS is between 1.4 and 2.3 TECU for the high- and mid-latitude sites which is a very promising result in our eyes. Not unexpectedly, the RMS climbs up to values of 7.2 and 10.7 TECU for MAS1 and MSKU, respectively. Horizontal interpolation errors and mapping function inconsistencies yield higher deviations from the reference data. The global RMS is close to 4 TECU taking all IGS LEO tracking sites into account. This is still in the 2–8 TECU boundaries of the uncertainty we have to expect for the reference data. However, please note that our statistical analysis can only depict the typical annual mean performance of the single-frequency VTEC retrieval algorithm. The accuracy of a single VTEC determination can still show variations, e.g., as a function of local time, which cannot be revealed by our analysis.
The long-term bias of MSKU is the largest out of all nine selected stations, but it is also located closest to the geomagnetic equator where the diurnal variations are strongest and gradients are most expressed. Moreover, this station had to largest number of data outages. Anyway, the bias is still much smaller in magnitude than the RMS of this station.
4. Galileo E5 test trials
As mentioned in Section 1.1, code range accuracy is of major importance to obtain useful VTEC results with this single-frequency algorithm. With this respect, the dominant error source is multipath. Table 1 summarizes maximum and typical multipath errors for selected signals for one specific type of correlator called “Narrow Correlator” (van Dierendock et al. 1992) as built into certain commercially available receivers.
Code range multipath errors for selected signals and receiver bandwidths (Eissfeller et al. 2007) assuming a GNSS receiver with built-in “Narrow Correlator” for multipath mitigation (the maximum error specifies the multipath envelope, the representative average errors is derived using a channel model).
The reader can see in the table that a number of new signals will be available. The GPS L5 signal, for instance, will also feature an increased multipath performance. Two modulation schemes have been developed for the Galileo E1 signal, one BOC (binary offset carrier; slightly different modulation scheme compared to GPS L1, but of similar overall performance) signal as well as a CBOC-modulated signal (a modified BOC signal) with slightly reduced multipath errors.
However, the Galileo E5 broadband signal will outperform all existing and future signals: It features minimum possible multipath errors. Maximum multipath errors of up to 1.6 m can be expected for E5 compared to more than 5 m for Galileo E1. Typical average E5 multipath code range errors in urban environments (strong multipath) should be in the range of around 0.3 m, but more than 2 m for Galileo E1 (CBOC). An ultimate performance of 4 cm could be reached in open environments where multipath errors are typically of lowest magnitude.
The improved code range precision will improve the code-carrier combination used for VTEC estimation in our single-frequency algorithm, of course. On the other hand, and in addition, the single-frequency single-site algorithm suffers from modeling errors which cannot necessarily be reduced by more precise observations, namely:
-
Inaccuracies related to the single-shell modeling approach, in particular the fixing of the effective height of the ionosphere that directly impacts the computation of the ionospheric pierce points and the computation of the mapping function.
-
The horizontal interpolation function is a source of error, because it will always exhibit a certain approximation error. This error is moderate in the mid-latitudes under typical conditions according to our experiences, but will grow under ionospheric storm conditions and the closer we get to the geomagnetic equator.
-
We currently assume that the Galileo E5 wideband signal will behave like a monochromatic wave, although it covers a broader spectrum of frequencies. This remains to be investigated in the future (Gao et al. 2007).
Note that biases are not considered to be a problem here, because these ones will be estimated as additional parameters and just are assumed to be stable for a couple of hours in our approach.
Despite these additional sources of error, it is undoubtedly desirable to use the most accurate code-carrier linear combination available. The Galileo E5 signal consequently offers an interesting alternative for the future. The following sections present some initial results underlining the benefit of this broadband signal.
4.1. Real-world data from GIOVE-B
The single-frequency VTEC estimator requires at least three well-distributed satellites to be observed simultaneously. This condition was not fulfilled at the time of this study: only two experimental Galileo satellites, GIOVE-A and B (we only present GIOVE-B results here), periodically broadcast the desired E5 signal. Nevertheless, we can illustrate the largely reduced noise characteristics of the E5 versus the E1 signal even with one single satellite using the “time-relative satellite-specific mode”. The algorithm used here is similar to that depicted by Yuan & Ou (2001). The only difference is that we are using IONEX data to determine the offset to level the relative data to absolute values, whereas Yuan and Ou use different models (e.g., Klobuchar) to do so.
Usable data on both E1 and E5 were available for the experimental satellite GIOVE-B (launch: 26 April 2008) on 12 January 2012 for a relatively long period of time. Data recording was done with a Septentrio PolaRx reference station receiver that makes use of the minimum necessary filter bandwidth of 51 MHz. The time series are plotted in Figure 4 (ZID: zenith ionospheric delay). The difference between the E1 and the E5 solutions is remarkable. The Galileo E5 time series is crystal-clear. The (random) noise level is extremely small, but one can still identify signatures that are most likely related to multipath effects rather than ionospheric fluctuations, but at a lower level of magnitude than the results based on the E1 signal. We have detrended these two time series with a polynomial of order 8 and analyzed the residuals in order to obtain a precision measure of the relative VTEC data. This yields a standard deviation of 0.33 TECU for the Galileo E1 and 0.13 TECU for the Galileo E5 results, a factor of 2.5 (and an improvement of 61%).
 |
Fig. 4. VTEC/ZID time series, Galileo/GIOVE-B E1 (left) and E5 (right), 12 January 2012 |
4.2. Simulated scenario (2006 Greece earthquake)
The 2006 Southern Greece earthquake occurred on 8 January 2006. The earthquake epicenter is shown on the map in Figure 5. Earthquake precursors can sometimes be sensed as a signal in the ionosphere under certain conditions, although the physics behind are not yet completely understood (Pulinets & Boyarchuk 2004) and are commonly considered to be a controversial issue. Anyway, for us, the main reason to select this event as a simulated test case in order to demonstrate the benefits of the Galileo E5 wideband signal is the following: Ionospheric earthquake precursors can only be identified under geomagnetically quiet conditions. Under such conditions, we can assume that the horizontal interpolation error of the single-site single-frequency VTEC estimation algorithm will be small, whereas the error will grow under disturbed conditions. Hence we are able to separate data modeling errors from observation uncertainties.
 |
Fig. 5. The 2006 Greece earthquake epicenter (large cross) and the four IGS/EUREF reference stations used in this test case. |
4.2.1. Data simulation
Simulated code range and carrier phase data for 7 days including several days before the seismic event were generated and analyzed. These synthetic observations were generated with a temporal resolution of 5 s. The further simulation settings are as follows:
The random carrier phase noise is set to a minimum of 0.6 mm and a maximum of 2 mm as a function of elevation. This corresponds to typical values for high-quality geodetic receivers. The code range noise is assumed to be 11 cm for Galileo E1 (identical choice for GPS L1) and 1 cm for Galileo E5 in zenith direction following Avila-Rodriguez et al. (2004, Table 6). These minimum noise figures are mapped into slant direction using an elevation-dependent exponential function so that measurements close to the horizon are considerably noisier than close to the zenith – an evident characteristic.
The multipath settings are taken from Eissfeller et al. (2007) and correspond to the values listed in Table 1: the maximum code range multipath is set to 6.93 m for Galileo E1 and 1.62 m for Galileo E5. The maximum carrier phase multipath errors are set to 23.8 mm for Galileo E1 and 31.4 mm for Galileo E5. The fact that Galileo E5 exhibits a higher maximum error on the carrier phase is linked to the phase shift induced by the multipath. Since the wavelength of E5 is higher (25.2 cm) compared to E1 (19.0 cm), the resulting error in metric units will be higher, too. However, all these error values for the carrier phases are of minor concern, because code range errors are clearly dominating. Similarly to the randomly distributed noise figure, an elevation-dependent increase of the multipath error is to be expected. In our simulation we assume that 32% of the maximum error are typically present at an elevation angle of 10°, and we set this ratio to 1.2% for values at zenith (which is rarely reached by the Galileo satellites). These percentages are taken from our experiences and approximately correspond to an environment at our University campus. Actually, we arrive at errors between 52 cm (at 10°) and (theoretically) 2 cm (at 90°) for the E5 signal which approximately fits the typical values stated in Table 1 for category “urban”. Note that the typical average elevation of a Galileo satellite is around 30° to 35°. With this respect, our simulation settings are relatively pessimistic, because there are also reference stations located in “open” environments. At these locations, the results obtained with Galileo E5 single-frequency data analysis could be significantly better than in our simulated scenario.
IGS IONEX maps were used to extract the ionospheric delay information and feed the simulator. Biases are present for each satellite and are always part of the estimation model of the single-frequency VTEC retrieval algorithm. As outlined before, no separation between receiver common biases and satellite-specific ones is carried out, i.e., individual biases are estimated for each uninterrupted satellite arc.
4.2.2. Results
Since we want to outline the benefit of the improved measurement precision of the Galileo E5 data, we restrict the results to a look at the standard deviation of unit weight à priori (σ0) and à posteriori (s0). The first is arbitrarily chosen as 1 m. The empirical à posteriori value is computed as s02 = vT × P × v, where v is the vector of residuals and P is the weight matrix. The results obtained with the Galileo E5 data are listed in Table 2.
Standard deviation of unit weight a posteriori (s0) for VTEC retrieval from synthetic Galileo E5 data; unit is meters.
It is to be stressed that the standard deviation of unit weight à posteriori is not only defined by the measurement precision only, but can also be influenced by data mismodeling effects, of course. However, we have intentionally chosen a geomagnetically quiet period of time in order to make sure that such modeling artifacts are reduced to sufficient extent, so that the results we see should be in major parts related to the measurement precision.
In average, the empirical standard deviation of unit weight is close to 10 cm for Galileo E5 and 38 cm for GPS L1 (not tabulated, because these values show little variability for the individual stations). This underlines the increased precision expected for the Galileo E5 broadband signal. Moreover, we can see that the minimum and maximum values in the case of GPS L1 only show very marginal variations, whereas the variations for the Galileo E5 results are higher (0.07 to 0.15 m). The explanation for this fact is actually related to the influence of modeling errors: These modeling uncertainties map into both standard deviations, but in the case of the GPS L1 results, these errors are more or less completely hidden by the relatively high observation noise, so the values do not show any strong numerical difference. This is a bit different from the Galileo E5 results. Here, the code range uncertainties are so small that modeling errors become visible in the numerical results. Consequently, the standard deviation of unit weight à posteriori can differ from day to day (and from site to site) depending on the individual ionospheric conditions introducing different modeling errors to the retrieval algorithm.
Clearly speaking, the mismodeling errors due to the limitations inherent in the horizontal interpolation algorithm and the mapping function (single-layer model of the ionosphere) will increase under unfortunate conditions such as ionosphere storms. In these cases, s0 will be in major parts influenced by these modeling errors so that the advantage of the improved code range precision of the E5 observations is likely not to yield a significant gain in the overall accuracy of the results. This is a limitation of the single-frequency single-site algorithm rather than of the Galileo E5 signal. The benefits of E5 wideband observations could still play an important role in network-based approaches in the future under such conditions.
5. Summary, conclusions, and outlook
The future global satellite navigation system Galileo will offer an outstanding signal in space, the E5 broadband signal, that will offer a code range accuracy, which is at least a factor of two up to a factor of 4 better than what we currently can expect from GPS L1 code range measurements. Unfortunately, this will be the only signal of that kind transmitted by the Galileo satellites. For this reason, we experimented with single-frequency single-site ionospheric delay estimation.
Despite the advances in measurement precision we expect from Galileo, we were surprised in a positive way by the VTEC results we could obtain from GPS real-world data for the year 2003. Comparing the estimated results with those of IONEX data from the IGS, a RMS of 4 TECU was obtained in global average. Most mid- and high-latitude stations even exhibit smaller RMS values of 1.5–2.5 TECU, whereas stations located within the geomagnetic equatorial belt normally show higher deviations.
Real data of the GIOVE-B experimental Galileo satellite were analyzed afterwards, demonstrating that a significant increase in measurement precision can be expected in the near future provided that the E5 AltBOC signal will be implemented in a similar manner as for GIOVE-B: the satellite-specific results for E5 are a factor of 2.5 less noisy than the results obtained from E1 data (what approximately corresponds to GPS L1 data). Unfortunately, there are not enough Galileo satellites in the sky yet (first half of year 2012) so that no absolute VTEC retrieval is possible with E5 data. Results for a geomagnetically quiet period of time from simulated observations confirm that the standard deviation of unit weight is significantly reduced for the Galileo E5 results compared to that of E1. We expect this advantage to diminish under disturbed conditions or when moving toward the geomagnetic equator. The reason for this fact is linked to the main data modeling errors inherent in the single-frequency single-site approach: inaccuracies related to the single-shell modeling approach directly impact the computation of the ionospheric pierce points and the computation of the mapping function. Moreover, the horizontal interpolation function is a source of error, because it will always exhibit a certain approximation error that will grow under disturbed conditions. Regarding the Galileo program, note that a full constellation of Galileo satellites is expected to be in place around 2020, but four IOV satellites should already be in orbit around the end of 2012 with an initial orbit configuration of 18 satellites to be ready around 2014–2016 (interested readers can find updates at the European Space Agency’s web site http://www.esa.int/esaNA/galileo.html – see “Galileo Fact Sheet (PDF)” (last access: 27 September 2012)).
Our future work regarding this single-site approach is to link the retrieval algorithm with the NeQuick2 ray-tracer. We hope to derive improved mapping function values via that method, and to better account for variations in the vertical structure of the ionosphere that is currently only modeled with one site-specific effective height of the ionosphere, fixed for the complete year.
Acknowledgments
The authors would like to thank the IGS community (International GNSS Service) for granting access to the high-rate dual-frequency GPS data of the IGS LEO network used in this study. The financial support of the European Union and the European GNSS Agency (GSA) in the framework of FP7 research grant “SX5 – Scientific Service Support based on Galileo E5 Receivers” is highly appreciated. Trademarks possibly mentioned in the text are the property of their respective owners.
References
- Avila-Rodriguez, J.-A., G.W. Hein, M. Irsigler, and T. Pany, Combined Galileo/GPS Frequency, Signal Performance Analysis, Proceedings of the International Technical Meeting of the Satellite Division of the Institute of Navigation, ION GNSS, September 21–24, Long Beach, California, pp. 632–649, 2004. [Google Scholar]
- Coco, D. S., C. Coker, S. R. Dahlke, and J. R. Clynch, Variability of GPS satellite differential group delay biases, IEEE Trans. Aerosp. Electron. Syst., 27 (6), 931–938, 1991. [CrossRef] [Google Scholar]
- Cohen, C.E., B. Pervan, and B.W. Parkinson, Estimation of absolute ionospheric delay exclusively through single-frequency GPS measurements, Proceedings of the 5th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1992), September 16–18, Albuquerque, NM, USA, pp. 325–329, 1992. [Google Scholar]
- Dach, R., U. Hugentobler, P. Fridez, and M. Meindl, Bernese GPS Software Version 5.0 (User manual of the Bernese GPS Software Version 5.0), AIUB – Astronomical Institute, University of Bern, January 2007. [Google Scholar]
- van Dierendonck, A.J., P. Fenton, and T. Ford, Theory and performance of narrow correlator spacing in a GPS receiver, Navig. J. Inst. Navig., 39 (3), 115–124, 1992. [Google Scholar]
- Doherty, P., A.J. Coster, and W. Murtag, Space weather effects of October to November 2003, GPS Solutions, 8 (4), 267–271, 2004. [CrossRef] [Google Scholar]
- Eissfeller, B., M. Irsigler, J. Avila-Rodriguez, E. Schüler, and T. Schüler, Das europäische Satellitennavigationssystem GALILEO – Entwicklungsstand, AVN – Allgemeine Vermessungsnachrichten, No. 02/2007, Wißner-Verlag, Germany, pp. 42–55, 2007. [Google Scholar]
- Gao, G.X., S. Datta-Barua, T. Walter, and P. Enge, Ionosphere effects for wideband GNSS signals, Proceedings of the 63rd Annual Meeting of The Institute of Navigation, Cambridge, pp. 147–155, 2007. [Google Scholar]
- Hoffmann-Wellenhof, B., H. Lichtenegger, and J. Collins, GPS – Theory and practice, 2nd ed., Springer, Wien, New York, ISBN 3-211-82364-6, 1993. [Google Scholar]
- Issler, J.-L., L. Ries, J.-M. Bourgeade, L. Lestarquit, and C. Macabiau, Probabilistic approach of frequency diversity as interference mitigation means, Proceedings of ION GNSS 2004, 17th International Technical Meeting of the Satellite Division, 21–24 September, Long Beach, CA, USA, pp. 2136–2145, 2004. [Google Scholar]
- Leick, A., GPS Satellite Surveying, 2nd ed., John Wiley & Sons, Inc, New York, ISBN 0-471-30626-6, 1995. [Google Scholar]
- Leick, A., GPS Satellite Surveying, 3rd ed., John Wiley & Sons, Inc, p. 464, ISBN 0-471-05930-7, 2004. [Google Scholar]
- Lestarquit, L., N. Suard, and J.-L. Issler, Determination of the ionospheric error using only L1 frequency GPS receiver, Proceedings of ION GPS-96, 9th International Technical Meeting of the Satellite Division of the Institute of Navigation, Kansas City Convention Center, September 17–20, Kansas City, USA, 1996. [Google Scholar]
- Mayer, C., N. Jakowski, J. Beckheinrich, and E. Engler, Mitigation of ionospheric range error in single-frequency GNSS applications, Proceedings of ION GNSS 2008, 21st International Technical Meeting of the Satellite Division, 16–19 September, Savannah, Georgia, USA, pp. 2370–2375, 2008. [Google Scholar]
- Nava, B., P. Coisson, and S. Radicella, A new version of the NeQuick ionosphere electron density model, J Atmos. Sol. Terr. Phys., 70 (15), 1856–1862, DOI: 10.1016/j.jastp.2008.01.015, 2008. [Google Scholar]
- Petit, G., B. Luzum, and IERS Conventions, IERS Technical Note No. 36. International Earth Rotation and Reference Systems Service (IERS), Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt am Main, 2010. [Google Scholar]
- Pulinets, S., and B. Boyarchuk, Ionospheric precursors of earthquakes, 1st ed., Springer, Berlin, ISBN 3-540-20839-9, 2004. [Google Scholar]
- Xia, R., Determination of absolute ionospheric error using a single frequency GPS receiver, Proceedings of the 5th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1992), September 16–18, Albuquerque, NM, USA, pp 483–490, 1992. [Google Scholar]
- Yuan, Y., and J. Ou, An improvement to ionospheric delay correction for single-frequency GPS users – the APR-I scheme, J. Geod., 75, 331–336, 2001. [CrossRef] [Google Scholar]
Cite this article as: Schüler T & Abel Oladipo O: Single-frequency GNSS retrieval of vertical total electron content (VTEC) with GPS L1 and Galileo E5 measurements. J. Space Weather Space Clim., 2013, 3, A11.
All Tables
Code range multipath errors for selected signals and receiver bandwidths (Eissfeller et al. 2007) assuming a GNSS receiver with built-in “Narrow Correlator” for multipath mitigation (the maximum error specifies the multipath envelope, the representative average errors is derived using a channel model).
Standard deviation of unit weight a posteriori (s0) for VTEC retrieval from synthetic Galileo E5 data; unit is meters.
All Figures
 |
Fig. 1. Map of the IGS high-rate reference stations used in the 2003 long-term data analysis experiment. |
| In the text | |
 |
Fig. 2. Selection of IGS network sites used for all diagrams in this paper; RMS “speedometer” visualization in (TECU) on the left and right. |
| In the text | |
 |
Fig. 3. Diagram of VTEC biases and RMS in (TECU) for the GPS L1 results. |
| In the text | |
 |
Fig. 4. VTEC/ZID time series, Galileo/GIOVE-B E1 (left) and E5 (right), 12 January 2012 |
| In the text | |
 |
Fig. 5. The 2006 Greece earthquake epicenter (large cross) and the four IGS/EUREF reference stations used in this test case. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


