| Issue |
J. Space Weather Space Clim.
Volume 4, 2014
|
|
|---|---|---|
| Article Number | A22 | |
| Number of page(s) | 7 | |
| DOI | https://doi.org/10.1051/swsc/2014020 | |
| Published online | 01 August 2014 | |
Regular Article
Scintillations of the GPS, GLONASS, and Galileo signals at equatorial latitude
1
German Aerospace Center (DLR), Institute of Communications und Navigation (IKN), Kalkhorstweg 53, 17235
Neustrelitz, Germany
2
Washera Geospace and Radar Science Laboratory, Bahir Dar University, Ethiopia
* Corresponding author: nikolai.hlubek@dlr.de
Received:
19
March
2014
Accepted:
4
July
2014
Small scale ionospheric disturbances can lead to fluctuations of the received satellite signal, so-called signal scintillations. For global navigation satellite systems (GNSS) this reduces the positioning accuracy. Particular strong events can even lead to a loss of lock between satellite and receiver. All GNSS signals are affected by this phenomenon. The influence of the short scale disturbances on the different GNSS signals is expected to be different for each signal, since the signals are transmitted by different carrier frequencies and are constructed in different ways. In this paper, we compare the occurrence rate of signal scintillations between the different global navigation satellite systems and their different signal frequencies. In particular, we consider GPS L1, L2, and L5, GLONASS L1 and L2, and Galileo E1 and E5a. This analysis uses data from a high-rate GNSS station of the German Aerospace Center (DLR) placed in Bahir Dar, Ethiopia at 11°36′ N 37°23′ E. The station collects 50 Hz raw data from which the amplitude scintillation index S4 is calculated. The data has been collected for the whole year 2013. Since the number of strong scintillation events with S4 > 0.5 was smaller than expected, additionally weak scintillation events with S4 ≥ 0.25 are taken into account. An algorithm is used that provides a soft barrier for S4 ≥ 0.25. The resulting events are shown as daily and seasonal averages. Finally, the overall influence of short scale ionospheric disturbances in the form of signal scintillations on the GNSS signals is estimated.
Key words: Ionosphere (equatorial) / Positioning system / Disturbances / Irregularities / Monitoring
© N. Hlubek et al., Published by EDP Sciences 2014
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
Since their inception the data of global navigation satellite systems have been used for scientific studies. For a long time only the American GPS and a partially functional Russian GLONASS were available for research. Now, GLONASS has reached full coverage and two new systems the European Galileo and the Chinese BeiDou are approaching a fully operational state. Furthermore the GPS is undergoing an upgrade that will provide a new civilian frequency.
From an ionospheric research point of view, the benefit of these new and enhanced systems is twofold. First, the increased number of satellites means more links to the ground receiver and thus additional pierce points through the ionosphere. This in turn corresponds to a higher number of measurement points for tomographic methods, which determine the total electron content of the ionosphere. Second, the new frequencies allow for a more detailed analysis of the dispersive nature of the ionosphere. While for a long time multi-frequency positioning was restricted to the military it becomes now also feasible for civilian users.
However, the benefits of these new or enhanced systems can still be severely limited, when the electromagnetic signal is diffracted by short scale structures in an irregular ionosphere and starts to fluctuate. These so-called signal scintillations usually decrease the positional quality, but in the worst case can lead to a loss of lock with the satellites on a receiver level Aarons (1997), Kintner et al. (2007), Kintner (2009). They can occur anywhere, but are very frequent in equatorial and polar regions. In the following we will focus on equatorial regions, where a strongly irregular ionospheric plasma in the evening hours produces mainly scintillations of the signal amplitude.
As scintillations may reduce positioning accuracy and can lead to loss of lock, which can delay or completely invalidate a positioning solution, basically every GNSS user is affected. Especially users that have high requirements for accuracy, integrity, availability, and continuity are affected. In short, all customers of augmentations services such as the European Geostationary Navigation Overlay Service (EGNOS) or the American Wide Area Augmentation System (WAAS). This includes e.g. prospecting work, geodetical undertakings and especially airport operations. At airports GNSS enable vertically guided approach procedures of aircrafts, which can be used instead of the traditional instrument landing system (ILS). GNSS systems are beneficial in this scenario, as the ILS is not suited for the requirements of modern high traffic airports. Since WAAS and EGNOS have been certified for the use in safety of life applications in 2007 and 2011, respectively, several prototype airports have started to deploy systems for GNSS landing and take-off. These prototype airports are in areas where scintillations occurrence is negligible Mayer et al. (2009), Circiu et al. (January 2014). However, further maturing of this technology will lead to its installation in regions with medium to high scintillation occurrence. Therefore an understanding of the rate of occurrence and strength of scintillations is necessary in order to properly certify these systems.
In this paper, we will analyze GNSS signal scintillations. Up to now, almost all studies of GNSS scintillations focused exclusively on the GPS L1 frequency Béniguel et al. (2009), SBAS Ionospheric Working Group (2010), Sreeja et al. (2011), Adewale et al. (2012), Paznukhov et al. (2012) with few authors considering GPS L2 and L5 Conker et al. (2003), Carrano et al. (2012), Shanmugam et al. (2012) and GLONASS L1, L2 Sreeja et al. (2012). To broaden this scope, we present results that compare the influence of scintillations on the new signals to GPS L1. An overview of the signals considered in this study is given by Table 1. All frequencies are in the L-band, which is a good compromise between signal attenuation at too high frequencies and ionospheric error at too low frequencies. Since the new signals will be used to enhance the position solution, it is necessary to know how they are influenced by scintillations and which signal is more trustworthy. Because the ionosphere is a dispersive medium and therefore scattering is dependent on the frequency, the amassed results from the GPS L1 signal cannot directly be transferred to the new signals that use different frequencies. The same is true when looking at the technical design of the signals. The different signals use different chipping rates, modulations and multiplexing techniques. All these factors might contribute to different robustnesses against signal scintillations and need to be investigated.
The table lists the frequencies in MHz of the GNSS and the particular channels studied in this article. GPS and Galileo use code division multiple access and therefore share one frequency for all satellites per channel. GLONASS uses frequency division multiple access and therefore has individual frequencies per channel per satellite given by the base frequency shifted by the frequency channel number (FCN).
The remainder of the paper is laid out as follows. After a short explanation how the statistical indices are derived, we will describe the setup of the measurement station. Then a discussion of a single scintillation event as experienced by one GPS satellite for its different signals follows. Next, we will present an algorithm that allows us to select all scintillation events in 2013 from our data set. This allows us to show a seasonal and daily average of the scintillation data. Finally, we will derive statistical values for each signal to estimate the impact of scintillations on the different systems and frequencies.
2. Statistical indices
Since the ionosphere is a non-linear system, the best way to get an initial insight is by employing a statistical approach and aggregating large amounts of measured data to classify relevant orders of magnitude and occurrence rates. A statistical index to characterize scintillation of the signal amplitude, which are predominant in equatorial areas, is defined by the scintillation index S4. Its definition allows to calculate a unique but characteristic amplitude scintillation index for each GNSS signal. In order to determine this index, usually the receivers in-phase and quadrature components I and Q are used to obtain the signal strength estimator wide band power. Then, by estimating the fluctuations in wide band power the S4 index can be derived by dividing the variance of the estimator by its mean value every 60s Van Dierendonck et al. (1993), Beach & Kintner (2001), Symeonidis et al. (2011).
A theoretical upper limit for S4 is 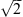 SBAS Ionospheric Working Group (2010). Numerically it is possible to produce larger values, but these are ignored as they indicate corrupt data. Regarding scintillation strength, for this paper, we consider 0.25 < S4 < 0.5 as weak and S4 > 0.5 as a strong scintillation event.
SBAS Ionospheric Working Group (2010). Numerically it is possible to produce larger values, but these are ignored as they indicate corrupt data. Regarding scintillation strength, for this paper, we consider 0.25 < S4 < 0.5 as weak and S4 > 0.5 as a strong scintillation event.
3. Measurement station setup
In this paper we use the data from our high-rate measurement station in Bahir Dar, Ethiopia, connected to the experimentation and verification network (EVNet) of DLR Noack et al. (2005). The station is situated at 11°36′ N 37°23′ E in the equatorial crest region. The station uses a JAVAD RingAnt-G antenna. This is a choke ring antenna which reduces the influence of multipath. The GNSS receiver is a JAVAD DELTA G3TH receiver that runs with an update rate of 50 Hz and is able to track GPS (L1, L2, L5), GLONASS (L1, L2), Galileo (E1, E5a), and BeiDou as well as the augmentation systems. It tracks all satellites in view, which are usually around 20. The receiver streams the incoming raw data to a connected computer, which runs our real-time scintillation analysis software. The software calculates the amplitude scintillation index S4 and the phase scintillation index σϕ for each signal. The indices are then streamed to the central processing and control facility of DLR Neustrelitz, where a visualization of the data for the SWACI platform1 is prepared. The results are shown afterwards on the web page and the data is archived for future analysis.
4. Results and discussion
Figure 1 shows a typical evening constellation of ionospheric pierce points in Bahir Dar Ethiopia. Looking at L1 (C/A)/E1, at first glance it seems as if enough unperturbed satellites are available for a positioning solution. However, it has to be noted that for GPS, only three satellites are unperturbed (5, 24, 29). All other GPS satellites are under the influence of weak to strong signal scintillations. Northwest of the GNSS receiver almost all pierce points show signal scintillation. This can be attributed to a strong ionospheric fluctuation, that moves outwards from the equatorial crest. Looking at the other frequencies, it is interesting to note, that the scintillation strength is stronger for all pierce points compared to L1 (C/A). In the following we will elaborate on this observation and discuss the statistics taken in 2013. We will show that L1 (C/A) is usually least affected by scintillations.
 |
Figure 1. Constellation of ionospheric pierce points at Bahir Dar Ethiopia. The blue cross marks the location of the receiver. The color of the pierce points corresponds to the strength of the amplitude scintillation S4 as indicated by the color bar below. The left half circle shows L1 (C/A)/E1. The right half circle shows GPS L5, GLONASS L2 and Galileo E5a, if available. The number next to the pierce point corresponds to the satellite id according to NMEA notation i.e. GPS: 1-32, GLONASS: 65-96, Galileo: > 200. |
Figure 2 shows the amplitude scintillation index S4 for the evening of the 11th April 2013 in Bahir Dar for GPS satellite G25. We choose satellite G25 since it is already modernized and thus able to broadcast on the new frequencies L5 and L2C. The different signals are shown in different colors. The most obvious observation is, that the scintillation indices for the encrypted precise code (p(y)-code) shown as crosses are generally much larger than those derived from the c-code. The deployed JAVAD receiver is not able to decode p-code, but uses z-tracking technology to reconstruct the L2 carrier phase. This degrades the signal-to-noise ratio Woo (2000). Hence, it is not surprising, that the reconstructed p-signal is more susceptible to noise and that the overall quality is worse. Additionally, this tracking mechanism is very prone to loss of lock. Therefore, for a better comparison of the different frequencies, we ignore the encrypted signals in the following. As it is no longer ambiguous, we abbreviate L1 (C/A) to L1 and L2C to L2 now.
 |
Figure 2. Comparison of the scintillation index S4 for the different signals of GPS satellite 25 at the 11th April 2013 in Bahir Dar, Ethiopia. The colored solid lines are averages of the S4 value in the time interval [18:00, 19:30] UTC. |
The difference between L1, L2, and L5 is small during the mostly undisturbed conditions after 20:00 UTC. For times later than 21:00 UTC all three signals converge to a mean scintillation value of S4 ≈ 0.04. However, at the peak of the scintillation event, at 19:00 UTC the difference between the three signals becomes quite large. The solid horizontal lines in the plot represent averages for the scintillation event in the time interval Tevent = [18:00, 19:30] UTC. These averages show that the GPS L1 signal is the least disturbed followed by L2 and then L5. This observation is a general trend in the data. The reason for this is the frequency dependence of scintillations, which is explained at the end of this article. Table 2 shows the mean S4 values and their standard deviations for the time interval Tevent. In addition to the already discussed averages it is noticeable that the standard deviation of L5 is much larger than those for L1 and L2. This is reflected in Figure 2 by a much stronger scattering of individual points for L5 compared to L1 and L2. It can be imagined that this stronger fluctuation is related to the 10 times higher chipping rate of L5 with regard to L1 and the corresponding longer code. A temporary signal unavailability causes a much higher data loss with a higher chipping rate and a longer code delays the acquisition and re-acquisition process, if the signal is weak or strongly fluctuating.
Averages and Standard deviation of GPS satellite 25 for 11th April 2013 between [18:00, 19:30] UTC.
All these observations give some expectations on the conclusions from the following analysis. Having discussed observations of one day and one satellite, now we will present averages for 2013 and for all satellites of the respective GNSS. To complicate matters for the analysis, the ionosphere in 2013 over Bahir Dar was surprisingly quiet with respect to scintillations. We did not find many events with S4 ≥ 0.5. Therefore, in order to make our statistics more reliable, we also considered weak scintillation events with S4 ≥ 0.25. Since this value is easily surpassed due to multipath effects at very low elevation angles, we removed values with elevations less than 20. Since Figure 2 shows that some signals fluctuate quite strongly during a scintillation event and we did not want to arbitrarily reduce these fluctuations by only considering values above S4 ≥ 0.25, we developed an algorithm that captures these fluctuations to a certain extent and which will be explained in the following.
First, all data with elevations lower than 20 are discarded. Next the data is cleaned by removing nonphysical values with S4 < 0 or 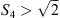 . Than the data is sorted. Afterwards, it is checked, if a minimum number of values μ for one satellite pass are larger than the event threshold τ (in our case μ > 5, τ = 0.25). This equals roughly 0.1% of the collected data of a satellite that passes close to the receiver. This criterion is used to remove unfavorable satellite geometries. That is, satellites which are only shortly in view and have a low elevation. These satellites can generate large values of S4, but it is very likely that these values derive from multipath effects. If the data set for a satellite pass has enough values that are larger than the threshold it is considered further. The algorithm then iterates over the data set. All values of S4 larger than τ are stored. Additionally, data points preceeding and following the stored values of S4 within a time-span γ = 300 s are stored as well. This form of soft cut-off allows to capture fluctuations close to the threshold τ and still removes unperturbed data reliably. Figure 3 shows the results of the algorithm for the same day as in Figure 2 for all GNSS and the L1/E1 signal. The small points are data points that have been removed by the algorithm, while the large ones are considered to belong to the scintillation event. It is easily visible that fluctuations around the threshold τ are not removed but kept. We use this algorithm to select the scintillation events from our Bahir Dar data for the whole year of 2013. The algorithm is not overly sensitive to τ, γ as the following seasonal and daily averages, as well as the aggregated statistical values, can be qualitatively reproduced with τ = [0.15, 0.5] and γ = [60, 600] s.
. Than the data is sorted. Afterwards, it is checked, if a minimum number of values μ for one satellite pass are larger than the event threshold τ (in our case μ > 5, τ = 0.25). This equals roughly 0.1% of the collected data of a satellite that passes close to the receiver. This criterion is used to remove unfavorable satellite geometries. That is, satellites which are only shortly in view and have a low elevation. These satellites can generate large values of S4, but it is very likely that these values derive from multipath effects. If the data set for a satellite pass has enough values that are larger than the threshold it is considered further. The algorithm then iterates over the data set. All values of S4 larger than τ are stored. Additionally, data points preceeding and following the stored values of S4 within a time-span γ = 300 s are stored as well. This form of soft cut-off allows to capture fluctuations close to the threshold τ and still removes unperturbed data reliably. Figure 3 shows the results of the algorithm for the same day as in Figure 2 for all GNSS and the L1/E1 signal. The small points are data points that have been removed by the algorithm, while the large ones are considered to belong to the scintillation event. It is easily visible that fluctuations around the threshold τ are not removed but kept. We use this algorithm to select the scintillation events from our Bahir Dar data for the whole year of 2013. The algorithm is not overly sensitive to τ, γ as the following seasonal and daily averages, as well as the aggregated statistical values, can be qualitatively reproduced with τ = [0.15, 0.5] and γ = [60, 600] s.
 |
Figure 3. Scintillation indices S4 for signals L1 (C/A)/E1 for all satellites tracked on 11th April 2013. The small dots are data points which have been removed by the soft-boundary algorithm and are not considered belonging to a scintillation event. |
Figure 4 shows the number of scintillation events per day over the course of the year 2013 for the different signals. The solid line represents a smoothed seasonal dependence. It was calculated by using a moving average filter on the data. The gray shaded area depicts the data availability. The curves visualize the strong seasonal dependence of scintillations. They are largest during the equinox periods, when the solar terminator is aligned with the magnetic meridian. At least for the African sector, this is known to increase the intensity of the prereversal enhancement Tsunoda (1985), Batista et al. (1986), Abdu et al. (1992), Tsunoda (2010), Alfonsi et al. (2013), which mostly controls the equatorial spread-F, producing a more perturbed ionosphere. A consistent trend for all the signals is, that the peak at the spring equinox is larger than that of the fall equinox. It is a reasonable assumption, that this is related to the activity of the sun. A good measure for this activity is the number of sunspots.2 If we consider 30 days around the equinoxes and calculate a mean number of sunspots, we get a value of 57.1 for the spring equinox and 44 for the fall equinox. This is roughly 30% more activity in spring, which in turn might contribute to the higher maximum. Looking at the related geomagnetics and thus the planetary Kp-index3 and doing the same analysis, we also find roughly 30% higher values for the time around the spring equinox, which can also contribute to a higher maximum. A more in depth study of the correlation between scintillations and solar and geomagnetic activity can be found in Liu et al. (2012).
 |
Figure 4. Amount of scintillation events over the course of the year 2013. The symbols are the accumulated time in minutes of scintillations per day for the respective signal. The black lines show a moving average. The gray shaded area marks the data availability. |
Figure 5 shows the frequentness of scintillation occurrence as a function of time of the day averaged for 2013. The color corresponds to the overall number of events that occurred at that minute (x-axis) equal or smaller the corresponding strength (y-axis). The colors red and yellow depict a large number of events, the color green an intermediate amount and white depicts no events at all. When creating these statistics, the change in the time for sunset during the course of the year has been taken into account. Everything has been shifted to a sunset time corresponding to 1st January 2013 which is 15:17 UTC.
 |
Figure 5. Aggregated statistics of scintillation occurrence in 2013 for the different signals as function of sunset corrected time. The dashed vertical lines indicate the time of sunset. |
An immediate observation is, that most of the scintillations occur at the evening hours. During this time the disturbance of the equatorial ionosphere is strongest. The principle source of this disturbance is the gravitational Rayleigh-Taylor instability i.e. the instability of a barrier between two media with different density. The literature on this effect is vast Farley et al. (1970), Aarons (1977), Basu & Basu (1981), Aarons (1982, 1993) with the first observation dating to 1934 Berkner & Wells (1934). The basic idea is that shortly post sunset, the lower density ionosphere at the bottom-side of the F layer rises into the higher density ionosphere above. This causes turbulence at the interface. Bubbles form in the plasma and percolate upwards, which leads to a strongly irregular ionosphere Kelley (1985). During the night this mechanism diminishes and the irregularities decay.
A more in-depth look at Figure 5 shows, that GPS L1 has scintillation events during the whole day. Additionally, it shows a double peak structure with one maximum close to 18:00 and the other one close to 20:00. A similar behavior is found for GPS L2, and with less intensity for GLONASS L1 and Galileo E1. This could indicate a general trend. GPS L5 does exhibit much less events and almost none during the day hours. Since up to now, only a few GPS satellites are able to broadcast L5 this is not surprising. GLONASS L1 shows a similar pattern to GPS L1. GLONASS L2 shows a large number of events during the course of the day and a broad maximum at the evening. This proves that GLONASS L2 is very susceptible to equatorial scintillations. Galileo E1 shows a similar pattern as GPS L1, albeit it has more outliers and is less smooth. As Galileo E5a shows a much smoother distribution this spikiness cannot be explained by the small number of satellites, but it might indicate a general susceptibility of the Galileo system towards equatorial scintillations. Galileo E5a shows events with large S4 values distributed throughout the day and thus indicates, that this frequency is strongly affected by equatorial scintillations.
Table 3 shows aggregated statistics for the various GNSS signals. The first column associates the overall mean of S4 to the lower limit for weak scintillations τ = 0.25 by the following formula: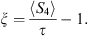 (1)
(1)
Aggregated statistics of scintillation occurrence for 2013. The first column gives an estimates of the overall influence of amplitude scintillations on the signals. The column “all” gives the total number of minutes with scintillations occurring as given by the algorithm in Figure 3. The column “sat” gives the average time a satellite that crossed Bahir Dar during times of scintillations was disturbed for 2013.
For this column only data collected between 16:00 UTC and 22:00 UTC were taken into account. A larger value corresponds to a stronger influence of amplitude scintillations on the signal. Although these statistics have a large error a trend is obvious. The L1 frequency generally has the smallest values. This indicates a fluctuation closer to the barrier τ and hence a smaller impact of scintillations on this frequency. The frequency L5 has the largest value for each system. It is strongly affected by scintillations. This frequency dependence is further highlighted in Figure 6. In this figure, 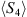 is shown as a function of frequency. According to experiments done by Ogawa et al. (1980) a frequency dependence S4 ~ f
−0.5 for 136 ≤ f ≤ 1700 MHz is expected. A fit to the data with this dependence is shown as solid red line. It is striking that only one fit parameter is needed. While this dependence can explain the data, one has to be careful with the interpretation of fits that contain only three distinct values. Therefore for comparison, additionally a linear fit is shown.
is shown as a function of frequency. According to experiments done by Ogawa et al. (1980) a frequency dependence S4 ~ f
−0.5 for 136 ≤ f ≤ 1700 MHz is expected. A fit to the data with this dependence is shown as solid red line. It is striking that only one fit parameter is needed. While this dependence can explain the data, one has to be careful with the interpretation of fits that contain only three distinct values. Therefore for comparison, additionally a linear fit is shown.
 |
Figure 6. Mean of S4 as function of frequency for the various signals. The solid lines are fits to the data. The inset shows the same results using double logarithmic axes. |
Column 3 of Table 3 lists the number of total scintillation events in minutes for each signal – i.e. the number of values with S4 > 0.25, including the soft barrier as discussed above. This number has to be taken with a grain of salt, since the number of satellites that can broadcast a specific signal varies for each signal. Still, it is interesting to note that GLONASS L2 and GPS L1 are affected by scintillations for the largest time span compared to the other signals. However, the strength of the actual influence on GPS L1, as seen in column one, is small. This mimics the overall trend in Figure 5. Roughly speaking, column one corresponds to the maximum of each of the subplots of Figure 5, while column two corresponds to the overall coverage and intensity in each of the subplots.
The fourth column of Table 3 gives an estimates of the number of events per satellite. Looking at one signal, this estimate is done by counting the number of satellites that were involved in scintillation events for a particular day. Afterwards the total number of events for that day is divided by this number. Then these satellite average scintillation times are aggregated for 2013. To put it simply, column four is an estimate for the total time, one satellite is disturbed. With the exception of GPS, the amount of time the individual satellites are influenced by scintillations is smallest for the L1/E1 signal. It is likely that the different result for GPS corresponds to the small number of upgraded GPS satellites with L2C and L5, which biases the statistics.
5. Summary
We have shown statistics of scintillation events for equatorial Africa for different GNSS signals. In particular we considered GPS L1, L2C, and L5, GLONASS L1, L2, and Galileo E1 and E5a. As a general trend we observed, that the magnitude of scintillations is smallest for the L1/E1 signals and largest for L5/E5a. We calculated statistics for the scintillation occurance during the course of a year. There we observed a double peak structure with the magnitude of scintillations largest during the spring and fall equinox. The peak is more pronounced at the spring equinox, which coincides with a higher solar activity and higher Kp-index. We calculated statistics for the average scintillation occurance for the course of a day. Generally, this gave the expected result that the scintillation occurance is highest after sunset. A more in dept look revealed two interesting results. First, the overall strength of scintillations is largest for Galileo. Second, the overall time a signal is affected is largest for GLONASS L2.
Acknowledgments
The SESAR Joint Undertaking within the frame of the SESAR Programme is co-financed by the EU and EUROCONTROL. The opinions expressed herein reflect the authors view only. The SESAR Joint Undertaking is not liable for the use of any of the information included herein. We thank the National Geophysical Data Center, Boulder, Colorado, USA for providing data for the International sunspot number and the Kp-index via ftp://ftp.ngdc.noaa.gov/STP. The editor thanks Marcio Muella and an anonymous referee for their assistance in evaluating this paper.
References
- Aarons, J., Equatorial scintillations: a review, IEEE Antennas Propag. Mag., 25 (5), 729–736, DOI: 10.1109/TAP.1977.1141649, 1977. [CrossRef] [Google Scholar]
- Aarons, J., Global morphology of ionospheric scintillations, Proc. IEEE, 70 (4), 360–378, DOI: 10.1109/PROC.1982.12314, 1982. [Google Scholar]
- Aarons, J., The longitudinal morphology of equatorial F-layer irregularities relevant to their occurrence, Space Sci. Rev., 63 (3–4), 209–243, DOI: 10.1007/BF00750769, 1993. [Google Scholar]
- Aarons, J., 50 years of radio-scintillation observations, IEEE Antennas Propagation Magazine, 39, 7–12, DOI: 10.1109/74.646785, 1997. [CrossRef] [Google Scholar]
- Abdu, M.A., I.S. Batista, and J.H.A. Sobral, A new aspect of magnetic declination control of equatorial spread F and F region dynamo, J. Geophys. Res. [Space Phys.], 97 (A10), 14,897–14,904, DOI: 10.1029/92JA00826, 1992. [Google Scholar]
- Adewale, A.O., E.O. Oyeyemi, A.B. Adeloye, C.N. Mitchell, J.A. R. Rose, and P.J. Cilliers, A study of L-band scintillations and total electron content at an equatorial station, Lagos, Nigeria, Radio Science, 47 (2), RS2011, DOI: 10.1029/2011RS004846, 2012. [CrossRef] [Google Scholar]
- Alfonsi, L., L. Spogli, M. Pezzopane, V. Romano, E. Zuccheretti, G. Defranceschi, M.A. Cabrera, and R.G. Ezquer, Comparative analysis of spread-F signature and GPS scintillation occurrences at Tucumán, Argentina, J. Geophys. Res. [Space Phys.], 118 (7), 4483–4502, DOI: 10.1002/jgra.50378, 2013. [Google Scholar]
- Basu, S., and S. Basu, Equatorial scintillations - a review, J. Atmos. Terr. Phys., 43 (5–6), 473–489, Equatorial Aeronomy – I, DOI: 10.1016/0021-9169(81)90110-0, 1981. [Google Scholar]
- Batista, I.S., M.A. Abdu, and J.A. Bittencourt, Equatorial F region vertical plasma drifts: seasonal and longitudinal asymmetries in the American sector, J. Geophys. Res. [Space Phys.], 91 (A11), 12,055–12,064, DOI: 10.1029/JA091iA11p12055, 1986. [Google Scholar]
- Beach, T., and P.M. Kintner, Development and use of a GPS ionospheric scintillation monitor, IEEE Trans. Geosci. Remote Sens., 39 (5), 918–928, DOI: 10.1109/36.921409, 2001. [Google Scholar]
- Béniguel, Y., J.-P. Adam, N. Jakowski, T. Noack, V. Wilken, J.-J. Valette, M. Cueto, A. Bourdillon, P. Lassudrie-Duchesne, and B. Arbesser-Rastburg, Analysis of scintillation recorded during the PRIS measurement campaign, Radio Science, 44 (1), RS0A30, DOI: 10.1029/2008RS004090, 2009. [Google Scholar]
- Berkner, L.V., and H.W. Wells, F-region ionosphereinvestigations at low latitudes, Terrestrial Magnetism and Atmospheric Electricity, 39 (3), 215–230, DOI: 10.1029/TE039i003p00215, 1934. [CrossRef] [Google Scholar]
- Carrano, C.S., K.M. Groves, W.J. McNeil, and P.H. Doherty, Scintillation Characteristics across the GPS Frequency Band, in: 25th International Technical Meeting of the Satellite Division of the Institute of Navigation, Nashville TN, September 17–21, pp.1972–1989, https://www2.bc.edu/~carranoc/carrano-ion-2465.pdf, 2012. [Google Scholar]
- Circiu, M.-S., M. Felux, P. Remi, L. Yi, B. Belabbas, and S. Pullen, Evaluation of Dual Frequency GBAS Performance using Flight Data, in: Proceedings of the 2014 International Technical Meeting of The Institute of Navigation, San Diego, California, 645–656, http://elib.dlr.de/88286/, 2014. [Google Scholar]
- Conker, R.S., M.B. El-Arini, C.J. Hegarty, and T. Hsiao, Modeling the effects of ionospheric scintillation on GPS/Satellite-Based Augmentation System availability, Radio Science, 38 (1), 1–1–1–23. DOI: 10.1029/2000RS002604, 2003. [CrossRef] [Google Scholar]
- Farley, D.T., B.B. Balsey, R.F. Woodman, and J.P. McClure, Equatorial spread F: implications of VHF radar observations, J. Geophys. Res., 75 (34), 7199–7216, DOI: 10.1029/JA075i034p07199, 1970. [CrossRef] [Google Scholar]
- Kelley, M., Equatorial spread-F: recent results and outstanding problems, J. Atmos. Terr. Phys., 47, 745–752, DOI: 10.1016/0021-9169(85)90051-0, 1985. [CrossRef] [Google Scholar]
- Kintner, P.M., B.M. Ledvina, and E.R. Depaula, GPS and ionospheric scintillations, Space Weather, 5 (9), S09003, DOI: 10.1029/2006SW000260, 2007. [CrossRef] [Google Scholar]
- Kintner, P.M.J., GNSS and Ionospheric Scintillation - How to Survive the Next Solar Maximum, in: InsideGNSS, July/August, 22–30, http://www.insidegnss.com/auto/julyaug09-kintner.pdf, 2009. [Google Scholar]
- Liu, Y.-H., C.-H. Liu, and S.-Y. Su, Global and Seasonal Scintillation Morphology in the Equatorial Region Derived from ROCSAT-1 In-situ Data, Terr. Atmos. Ocean. Sci., 23, 95–106, DOI: 10.3319/TAO.2011.06.30.01(AA), 2012. [CrossRef] [Google Scholar]
- Mayer, C., B. Belabbas, and W. Dunkel, Ionospheric Threat Model Assessment, in: ICAO NSP Meeting, 2009-03-17-2009-09-20, EUROCONTROL Experimental Centre, Bretigny (France), http://elib.dlr.de/58489/, 2009. [Google Scholar]
- Noack, T., E. Engler, and D. Klähn, High Rate Performance, Assessment of GNSS Raw Data Based on the DLR Experimentation and Verification Network, in: Proceedings of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), September, Long Beach, CA, 573–583, http://elib.dlr.de/18935/, 2005. [Google Scholar]
- Ogawa, T., K. Sinno, M. Fujita, and J. Awaka, Severe disturbances of VHF and GHz waves from geostationary satellites during a magnetic storm, J. Atmos. Terr. Phys., 42 (7), 637–644, http://www.sciencedirect.com/science/article/pii/0021916980900987, 1980. [CrossRef] [Google Scholar]
- Paznukhov, V.V., C.S. Carrano, P.H. Doherty, K.M. Groves, R.G. Caton, et al., Equatorial plasma bubbles and L-band scintillations in Africa during solar minimum, Ann. Geophys., 30 (4), 675–682, http://www.ann-geophys.net/30/675/2012/, 2012. [Google Scholar]
- SBAS Ionospheric Working Group Effect of Ionospheric Scintillations on GNSS - A White Paper, http://waas.stanford.edu/papers/IWG/sbas_iono_scintillations_white_paper.pdf, 2010. [Google Scholar]
- Shanmugam, S., J. Jones, A. MacAulay, and A.V. Dierendonck, Evolution to Modernized GNSS Ionospheric Scintillation and TEC Monitoring, in: Proceedings of IEEE/ION PLANS, Myrtle Beach, South Carolina, April 2012, pp. 265–273, DOI: 10.1109/PLANS.2012.6236891, 2012. [Google Scholar]
- Sreeja, V., M. Aquino, Z.G. Elmas, and B. Forte, Correlation analysis between ionospheric scintillation levels and receiver tracking performance, Space Weather, 10 (6), 1–2, S06005, DOI: 10.1029/2012SW000769, 2012. [CrossRef] [Google Scholar]
- Sreeja, V.V., M. Aquino, B. Forte, Z. Elmas, C. Hancock, et al., Tackling ionospheric scintillation threat to GNSS in Latin America, J. Space Weather Space Clim., 1 (1), A05, DOI: 10.1051/swsc/2011005, 2011. [CrossRef] [EDP Sciences] [Google Scholar]
- Symeonidis, D., J. Fortuny-Guasch, C. O’Driscoll, and A.B. Martinez, Scintillation Parameter Estimation Using Unmodified Professional GNSS Receivers: a Feasibility Study, in: Proceedings of the 24th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2011), Portland, OR, September, 2580–2587, http://azimout.dyndns.org/pdfs/scintillation_parameter_estimation.pdf, 2011. [Google Scholar]
- Tsunoda, R.T., Control of the seasonal and longitudinal occurrence of equatorial scintillations by the longitudinal gradient in integrated E region Pedersen conductivity, J. Geophys. Res. [Space Phys.], 90 (A1), 447–456, DOI: 10.1029/JA090iA01p00447, 1985. [Google Scholar]
- Tsunoda, R.T., On equatorial spread F: establishing a seeding hypothesis, J. Geophys. Res. [Space Phys.], 115 (A12), A12303, DOI: 10.1029/2010JA015564, 2010. [CrossRef] [Google Scholar]
- Van Dierendonck, A., J. Klobuchar, and Q. Hua, Ionospheric Scintillation Monitoring Using Commercial Single Frequency C/A Code Receivers, in: Proceedings of the 6th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GPS 1993), September Salt Lake City, UT, 1333–1342, http://www.ion.org/publications/abstract.cfm?articleID=4318, 1993. [Google Scholar]
- Woo, K., Optimum Semi-Codeless Carrier Phase Tracking of L2. NAVIGATION, Journal of The Institute of Navigation, 47, 82–99, http://www.ion.org/publications/abstract.cfm?jp=j&articleID=2272, 2000. [CrossRef] [Google Scholar]
Cite this article as: Hlubek N, Berdermann J, Wilken V, Gewies S, Jakowski N, et al.: Scintillations of the GPS, GLONASS, and Galileo signals at equatorial latitude. J. Space Weather Space Clim., 2014, 4, A22.
All Tables
The table lists the frequencies in MHz of the GNSS and the particular channels studied in this article. GPS and Galileo use code division multiple access and therefore share one frequency for all satellites per channel. GLONASS uses frequency division multiple access and therefore has individual frequencies per channel per satellite given by the base frequency shifted by the frequency channel number (FCN).
Averages and Standard deviation of GPS satellite 25 for 11th April 2013 between [18:00, 19:30] UTC.
Aggregated statistics of scintillation occurrence for 2013. The first column gives an estimates of the overall influence of amplitude scintillations on the signals. The column “all” gives the total number of minutes with scintillations occurring as given by the algorithm in Figure 3. The column “sat” gives the average time a satellite that crossed Bahir Dar during times of scintillations was disturbed for 2013.
All Figures
 |
Figure 1. Constellation of ionospheric pierce points at Bahir Dar Ethiopia. The blue cross marks the location of the receiver. The color of the pierce points corresponds to the strength of the amplitude scintillation S4 as indicated by the color bar below. The left half circle shows L1 (C/A)/E1. The right half circle shows GPS L5, GLONASS L2 and Galileo E5a, if available. The number next to the pierce point corresponds to the satellite id according to NMEA notation i.e. GPS: 1-32, GLONASS: 65-96, Galileo: > 200. |
| In the text | |
 |
Figure 2. Comparison of the scintillation index S4 for the different signals of GPS satellite 25 at the 11th April 2013 in Bahir Dar, Ethiopia. The colored solid lines are averages of the S4 value in the time interval [18:00, 19:30] UTC. |
| In the text | |
 |
Figure 3. Scintillation indices S4 for signals L1 (C/A)/E1 for all satellites tracked on 11th April 2013. The small dots are data points which have been removed by the soft-boundary algorithm and are not considered belonging to a scintillation event. |
| In the text | |
 |
Figure 4. Amount of scintillation events over the course of the year 2013. The symbols are the accumulated time in minutes of scintillations per day for the respective signal. The black lines show a moving average. The gray shaded area marks the data availability. |
| In the text | |
 |
Figure 5. Aggregated statistics of scintillation occurrence in 2013 for the different signals as function of sunset corrected time. The dashed vertical lines indicate the time of sunset. |
| In the text | |
 |
Figure 6. Mean of S4 as function of frequency for the various signals. The solid lines are fits to the data. The inset shows the same results using double logarithmic axes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


