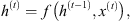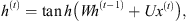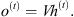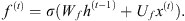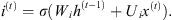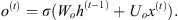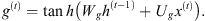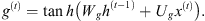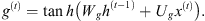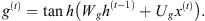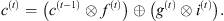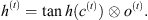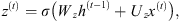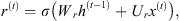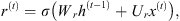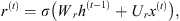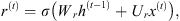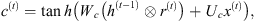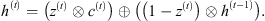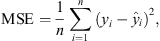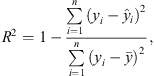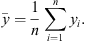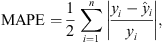| Issue |
J. Space Weather Space Clim.
Volume 12, 2022
|
|
|---|---|---|
| Article Number | 19 | |
| Number of page(s) | 23 | |
| DOI | https://doi.org/10.1051/swsc/2022015 | |
| Published online | 14 June 2022 | |
Research Article
Exploring possibilities for solar irradiance prediction from solar photosphere images using recurrent neural networks
1
National Institute for Space Research, Av. dos Astronautas, 1758 São José dos Campos, Brazil
2
Federal Institute of Education, Science and Technology of São Paulo, Route Presidente Dutra km 145 – Jardim Diamante, São José dos Campos, Brazil
* Corresponding author: amita.mk@gmail.com
Received:
22
June
2021
Accepted:
10
May
2022
Studies of the Sun and the Earth’s atmosphere and climate consider solar variability as an important driver, and its constant monitoring is essential for climate models. Solar total and spectral irradiance are among the main relevant parameters. Physical semi-empirical and empirical models have been developed and made available, and they are crucial for the reconstruction of irradiance during periods of data failure or their absence. However, ionospheric and climate models would also benefit from solar irradiance prediction through prior knowledge of irradiance values hours or days ahead. This paper presents a neural network-based approach, which uses images of the solar photosphere to extract sunspot and active region information and thus generate inputs for recurrent neural networks to perform the irradiance prediction. Experiments were performed with two recurrent neural network architectures for short- and long-term predictions of total and spectral solar irradiance at three wavelengths. The results show good quality of prediction for total solar irradiance (TSI) and motivate further effort in improving the prediction of each type of irradiance considered in this work. The results obtained for spectral solar irradiance (SSI) point out that photosphere images do not have the same influence on the prediction of all wavelengths tested but encourage the bet on new spectral lines prediction.
Key words: Solar irradiance / TSI / SSI / Recurrent neural network / LSTM / GRU
© A. Muralikrishna et al., Published by EDP Sciences 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The total power output of the Sun, which is radiated to space, the solar luminosity, results from the energy generation in and transport from the solar interior to its surface (Stein, 2012), and its variability on time scales of days to centuries is caused by the evolution of the solar magnetic structure (Solanki et al., 2013). The solar electromagnetic output that reaches the top of the Earth’s atmosphere is the system’s primary energy source (Kren et al., 2017), including the neutral and ionized components of the atmosphere, the oceans, and the land. Here, we are interested in studying predictive models of the evolution of the solar electromagnetic output that potentially impacts the Earth’s atmosphere on time scales from days to weeks.
While it is impossible to measure the luminosity directly with the current observatories, measurements of total solar irradiance (TSI) have been available since 1978 (Hickey et al., 1988). Solar irradiance is defined as the solar radiant energy flux arriving at the top of the terrestrial atmosphere at a distance of 1 AU1 (Willson et al., 1981). It has the potential to affect the terrestrial climate and is, therefore, an important parameter in climate models (Haigh, 2007; Gray et al., 2010; Ermolli et al., 2013; Solanki et al., 2013; Matthes et al., 2017).
Solar irradiance is absorbed in different layers of the Earth’s atmosphere, depending on the wavelength. Variations of the spectral solar irradiance (SSI), which is the solar irradiance at a given wavelength, potentially drive changes in the upper atmosphere and ionosphere (Haigh, 2007). Therefore, estimating the spectrally resolved irradiance is essential to evaluate the solar impact on global and regional atmospheric patterns.
Direct measurements of the total and spectral solar irradiance have been performed employing instruments onboard space platforms (Rottman et al., 1993; Fröhlich et al., 1997; Ermolli et al., 2013; Kopp, 2016; DeLand et al., 2019). However, discrepancies between measurements collected by various equipment sometimes complicate obtaining long and continuous data records due to calibration and temporal degradation of the equipment (Yeo et al., 2014).
Empirical and semi-empirical models have been developed which rely (fully or partly, respectively) on proxies of the solar magnetic activity, such as sunspot observations and cosmogenic isotopes stored in natural records (Krivova et al., 2010; Ball et al., 2014; Wu et al., 2018). These models allow us to reconstruct the irradiance from days to the entire Holocene (Steinhilber et al., 2009; Vieira et al., 2011b). Models can also be used to fill in missing data.
Although these models can reproduce the TSI/SSI accurately, they have not yet incorporated a predictive capability. Such capability would be possible if the distribution of magnetic features on the far-side solar hemisphere were available. Alternatively, one can predict the behavior of the variable of interest using a combination of past values of the variable and other proxies. The solar irradiance prediction would be important, for example, for ionospheric models (Nogueira et al., 2015), to improve their predictive capabilities hours or even days earlier.
One approach to predict solar irradiance was first proposed by Vieira et al. (2011a), whose approach was conceptually inspired by a class of semi-empirical models that employ observations of the solar surface magnetic field and continuum images to compute the TSI/SSI (Fligge et al., 1998; Krivova et al., 2010; Ball et al., 2011; Fontenla et al., 2011). The forecast of the TSI/SSI is obtained by combining a basic architecture of a recurrent artificial neural network and a physics-based model. The resulting neural network was tested in operational conditions as part of the SOTERIA Project at LPC2E/CNRS and within The Space Weather Program at the Brazilian National Institute for Space Research. The concept proved to be consistent, but it is still necessary to explore different neural network architectures and optimization methods.
Our main objective in this work is to extend the workflow suggested by Vieira et al. (2011a) to predict total and spectral solar irradiance to a time window from hours to days. We developed the experiments by performing and training two different recurrent neural network gated architectures – LSTM (Long Short-Term Memory) and GRU (Gated Recurrent Unit) – and the results were compared to the physics-based semi-empirical SATIRE (Yeo et al., 2014) and empirical EMPIRE (Yeo et al., 2017) models.
For this work, three wavelengths were chosen for the spectral irradiance prediction: one emission line of hydrogen, the Lyman-α (121.5 nm), and two helium wavelengths (30.5 nm and 48.5 nm). The decision to choose these wavelengths was motivated by the influence of one of them (Lyman-α) on the formation of the ionosphere, the Earth’s ionized layer (Raulin et al., 2013), and the other two for providing a diagnosis of solar activity. However, the workflow is designed to accept other desired wavelengths.
It is worth mentioning that there are some commercial options for irradiance prediction, such as SOLAR2000, a commercial system with an operational purpose that predicts spectral solar irradiance, from the X-rays to the infrared wavelengths. SOLAR2000 uses solar proxies for the estimations in different time intervals. Its initial version is described by Tobiska et al. (2000), and it was updated in 2006 by Tobiska & Bouwer (2006). Herrera et al. (2015) offer another commercial option, which uses the PMOD and ACRIM TSI composites and relies on Support Vector Machines Supporting Least Squares to predict the TSI. The wavelet transform is also employed to analyze the behavior of the irradiance time series before and after the large solar minima. This work, however, aims to provide a free workflow for the scientific community. For this reason, we developed a workflow in Python, an open and multi-platform programming language, with the purpose of making it available to contribute to future research projects that may have an interest in reusing it partially or totally and to make it as reproducible as possible. The source code and other resources used in this work were available in a GitHub repository.2
2 Recurrent neural networks
Recurrent neural networks (RNN) are a type of artificial neural networks (ANN) with a dynamic behavior during their training, which considers and explores the existing dependency between their input instances. This feature is the main difference between the RNNs and the traditional feed-forward ANNs, which deals with the inputs independent of each other. In this recurrent architecture, the output of a neuron (commonly called “unit”) can be fed back into the unit itself (Goodfellow et al., 2016). This special feature allows the RNNs to be used in language processing problems such as speech recognition, language modeling, machine translation (Gulli & Pal, 2017), price monitoring (Pinheiro & Senna, 2017), and time series analysis in general, cases in which considering the historical context of the inputs can be an essential differential for the forecast accuracy.
Besides the traditional matrix of weights used to weight the inputs of hidden or output neurons on conventional ANNs, the simple types of RNNs have matrices of weights used exclusively in the processing of the feedback coming from the previous processing moments.
The recurrent net basic process calculates each recurrent unit state h in the time instant t, given the input at the same time x(t) and the unit’s previous state h(t−1), generating the unit’s output o(t). For this process, three weight matrices are used: U and V as the input and the output weight matrices, respectively, and W as the weight matrix applied to the feedback signals (Goodfellow et al., 2016). Such process’ operations can be formalized as follows:
Traditional artificial neural networks, like multilayer perceptrons, use different versions of backpropagation (Chauvin & Rumelhart, 1995) as their training algorithm; some of them are described in Chauvin & Rumelhart (1995). In the case of RNNs, the training algorithm normally used is backpropagation through time (BTT), adapted from the traditional backpropagation, which can work with the input temporal dependencies for the backward propagation of errors process.
Although the BTT can store inputs already processed in the past to positively influence the processing of current inputs towards the desired output, the back-propagated error begins not to interfere significantly in the weights’ adjustment, bringing the learning problem of vanishing gradient (Hochreiter, 1998), which the simplest recurring networks cannot deal with, as confirmed in Muralikrishna et al. (2020).
This problem motivated improvements in the basic RNN algorithm, creating a variation of RNN with a gate structure, among which the main and most used today are LSTM and GRU.
2.1 LSTM
LSTM networks, proposed by Hochreiter & Schmidhuber (1997), are composed of memory units that have an advanced structure of gates, which “protect” internal processing from disturbances arising from irrelevant inputs and stored irrelevant memory contents (Hochreiter, 1998). The same structure is also present in the GRU network but in a more compact form.
The LSTM network can learn long-term dependencies with more interactions in the recurrent units processing (Hochreiter, 1998). The memory block is the basic unit in the hidden layer of an LSTM network, composed of one or more memory units and of gates that control the input and output of these units. The hidden internal state is computed based on the current input and the previous state of the neuron, similar to what happens in the elements of simple RNNs, and the gates are:
-
Forget Gate f(t): Defines how much of the previous state h(t − 1) should be allowed to pass through, given by:
-
Input Gate i(t): Defines how much of the newly computed state for the current input x(t) will be let go, given by:
-
Output Gate o(t): Defines how much of the internal state h(t−1) is desired to be exposed for the next layer, given by:
These three gate outputs are activated by the sigmoid function, falling in a range from zero to one. After multiplying the output by a second vector, the function will define how much of it will be passed through it.
Internal Hidden State g(t): It is computed based on the current entry x(t) and the previous state h(t − 1) of the neuron, using the function tanh, similar to what happens in the basic RNN’s unit (Eq. (7)). However, in this case, g(t) will be adjusted by the input gate output i(t), during the so-called “cell-state” computation, as follows:
The cell-state (c(t)) is given by equation (8), in which a combination is made between the long-term memories and the most recent ones through the Forgot and the Input gates. This way, their values are weighted in order to ignore the desired memories (with value 0) or make them relevant (with value 1), as follows:
The output h(t) of the neuron is finally calculated as follows, as a function of c(t), after applying the tanh function to it and then determining, through the value of the output gate, how much this output is relevant to such time instant:
2.2 GRU
It can be considered that the GRU network is a variation of the LSTM network and very similar to it proposed by Cho et al. (2014), with the advantage of having a considerably simpler gates structure than LSTM. A GRU is composed of only two gates:
Update
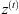 , which integrates the LSTM forget and input gates, which is able to be trained to define how much of the older information should be kept (Gulli & Pal, 2017), and
, which integrates the LSTM forget and input gates, which is able to be trained to define how much of the older information should be kept (Gulli & Pal, 2017), andReset
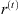 , which is able to be trained to merge the new information entries with the previous memories (Gulli & Pal, 2017).
, which is able to be trained to merge the new information entries with the previous memories (Gulli & Pal, 2017).
The following equations, given by Gulli & Pal (2017), summarize the computations that take place in GRU cells:
According to some works, like in Jozefowicz et al. (2015), LSTM and GRU are networks that have shown themselves to be very similar in terms of performance. In this work, we try to perform solar irradiance prediction using recurrent neural networks. Both architectures – LSTM and GRU – will be tested to determine which will bring better results for the forecast task.
3 Model description
The conditions of the Earth’s upper atmosphere are influenced by solar activity and are sensitive to its high variability (Vieira et al., 2011a). The prediction of solar irradiance measured at the top of the Earth’s atmosphere could confirm this dependence and help predict the Earth’s atmosphere layers behavior and provide data for other types of Earth’s climate-related studies, as mentioned before.
In this work, we intended to perform the total and spectral solar irradiance prediction procedure developed by Vieira et al. (2011a), which used the proprietary software Windows and Matlab. Vieira et al. (2011a) employed a recurrent layer available in the Matlab neural network toolbox to perform the near-real-time forecast of solar irradiance (neural network’s output), using as input the solar disk magnetograms and intensity images. The magnetic structures present in those images were identified and classified according to the area of the solar disk covered by them. The position of the structures identified in the solar disk was also considered for the neural network’s input data preparation.
We aimed to replicate Vieira et al. (2011a)’s approach but used free software, as the first step of the future aim of making the irradiance prediction workflow reproducible. In other words, we are working to create a procedure that can be re-executed by another researcher or research group without the dependence on any acquisition of resources but using only free software.
Reproducibility is a feature increasingly expected in scientific papers nowadays since it brings, foremost, transparency and credibility to scientific work (McNutt, 2014). However, at the same time, when we look for a definition of what a reproducible work is or how it can be measured, we can find different contexts, which may vary according to the discipline or the type of research (Li et al., 2011; Aarts et al., 2015; Fidler & Wilcox, 2021). In the context of computational works, which this work fits into, the definition is given by Rougier et al. (2017): “Reproducing the result of a computation means running the same software on the same input data and obtaining the same results.” is the one we have chosen that best fits our goal of making the work available so that it can not be reproduced only, but also be reused with other data or with other techniques, for instance.
The next subsections describe the input and output data used in the workflow and the flow’s steps until the prediction task.
3.1 Data
Different instruments and missions collected the data used in this work. Solar photosphere image data sets were collected by HMI (Helioseismic and Magnetic Imager) instrument aboard the SDO3 (Solar Dynamics Observatory) mission, and TSI measures were collected by the instrument TIM (Total Irradiance Monitor) aboard the SORCE4 (Solar Radiation and Climate Experiment) mission. The hydrogen Lyman-α line (at 121.5 nm) and the 30.5 nm wavelength were collected by the instrument SOLSTICE (Solar Stellar Irradiance Comparison Experiment) aboard the SORCE, and the wavelength (48.5 nm) was collected by EVE (Extreme Ultraviolet Variability Experiment), an SDO equipment.
All data were free downloaded from two different repositories: the photosphere images are available on the JSOC (Joint Science Operations Center) data products5 database, and the irradiance data are made available on the LISIRD6 (LASP Interactive Solar Irradiance Data Center) platform, hosted on the LASP (Laboratory for Atmospheric and Space Physics) website.
The solar photosphere images used were 1024 × 1024 pixels 1K resolution magnetograms (with the suffix M_1k.jpg) and continuum images (with the suffix Ic_flat_1k.jpg). The top images of Figure 1 are an example of both, recorded in the same instant of time: 6:00 AM on 2011, November 9th, and the images above are the results of the upper images after executing the identifying step of the workflow (this step is indicated in Figure 2). The magnetogram (Fig. 1b) allows the visualization of active regions with light and dark zones, which represent the opposite polarities of the magnetic field in those places; and the continuous image (Fig. 1a) shows the sunspots, formed by regions of umbra (in the center) and penumbra (around the umbra region).
 |
Fig. 1 Top: continuum image with sunspots (a), and magnetogram with active regions (b), both registered at the same time (6:00 AM) on 9 November 2011 by HMI/SDO. Bottom: results of running the workflow initial step on the images shown at the top, with umbra and penumbra regions (c) and active regions with different dimensions (d) identified. |
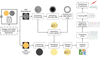 |
Fig. 2 Workflow for processing the solar images and predicting solar irradiance. |
3.2 Workflow steps
The workflow can be briefly described as loading solar photosphere images, identifying disturbed regions, classifying them according to their size and the locality where they appear in the solar disk, and then preparing those partial results to be used as input data to the chosen forecasting technique (Vieira et al., 2011a). The original algorithms were maintained but were rewritten in Python programming language and started to be rearranged to provide a modular structured workflow. The modular structure can be thought of as a structure that allows each workflow’s task to be executed independently and thus is exchanged for other task options that use other algorithms, methods, or techniques.
The workflow’s steps are summarized in Figure 2 and, in more detail, consist of:
Downloading the magnetograms and continuum images;
Identifying and delimiting the solar disk region;
Creating a mask to split the solar disk into eleven rings (circumferences) from the disk’s center to its edge;
Processing the magnetogram: within the solar disk region, identifying connected subregions (active regions), labeling each subregion by its area sizes;
Processing the continuum image: identifying the dark pixels subregions and labeling them into penumbra (less dark) and umbra (darker);
Joining the labeled matrices of the magnetogram and the continuous image into a single matrix, with six types of structures – four size categories of active regions structures, the penumbra structure and the umbra structure;
For each of the six labels:
Computing the label’s relative frequency based on the total amount of pixels in the solar disk;
Computing that label’s relative frequency in each of the regions formed by the disk’s eleven rings, based on the total number of pixels in the image;
Saving the resulted array, with dimension 6 × 11, considering a sum of areas of each of the six classes within each of the eleven rings;
Reading the irradiance data file and selecting the data according to the chosen irradiance type;
Choosing the labels and rings that will be considered for use as input to the RNNs. In this step, the first two classes of regions – small and medium – and the last outer ring of the disk are discarded since it is considered that they may bring information not relevant to the prediction. This resulted in a N × 40 matrix (four classes into 10 rings), where N is the number of images processed;
Preparing the input matrices, considering the predicting intervals;
Preparing the net’s hyperparameters;
Training, validating and testing, and
Displaying and saving the results.
Figure 3 is a set of plots for two months of the training data set, where the six top plots show the number of pixels labeled as active regions with different sizes – small, medium1 (or “medium-small”), medium2 (or “medium-large”), and large – in the magnetograms, and as sunspots umbra and penumbra regions in the continuum images. The following four plots below show TSI and SSI for the same time frame.
 |
Fig. 3 Part of the training data set: amount of pixels for active regions, umbra and penumbra, TSI and SSI variation, measured in November and December 2011. |
Considering the combinations of six classes of regions – of which four represent different sizes of active regions, one represents umbra regions, and the last represents penumbra regions – and eleven solar disk rings, we should have 66 parameters for each input instance. But, the solar disk’s most outer ring could present distorted pixels as it is near the disk edge. Besides that, the original procedure considered that the two smaller classes of regions have no significant influence on the solar activity scenario, specially for this work. Taking this into consideration, the classification step returns a 4 × 10 numerical matrix. Those values are the total areas of the combination of active regions and sunspots classified in four different sizes in ten different regions (rings) of the solar disk. Therefore, at last, as the final workflow step, for each pair of solar images representing a single instant of time, forty parameters were generated to be presented as input to the network. These inputs were used to predict a single irradiance value hours or days ahead.
4 Experiments and results
Once the workflow had been developed, it was possible to perform different prediction experiments, varying the input and output data for this study. This section will describe the experiments performed and present their main results.
RNNs, like traditional neural networks, compare real data to the values calculated (predicted) by the network in the output to adjust the internal weights and repeat the processes until the error between real and predicted is acceptable. To do so, they go through three phases: training and validation, which are used to seek convergence, and testing, which allows the network’s performance to be evaluated for another still unknown data set.
4.1 Data intervals and resolution
The experiments started with defining the temporal resolution of the data and the data periods used during the networks’ training, validation, and testing phases. The workflow input images were used at 6 h resolution, while the SSI and TSI series were used in two different resolutions: for TSI, the resolution was of 6 h for all the experiments, and for SSI, the single resolution was of one day (daily average).
The data sets’ (Figure 4) periods were chosen mainly, taking into consideration their continuous availability to avoid large failure periods, both in the input images and in the time series used in the output, thus also avoiding the need for large interpolations. In the output data, interpolations were used only to fill a maximum of four consecutive time instants of failure. On the other hand, missing images were replaced with 15-minute resolution images of up to 3 h back and forward. However, image replacements and data interpolations were required for less than 0.5% of the data.
 |
Fig. 4 Data intervals used for the RNNs training, validation and test steps, considering the period near the 24th solar cycle maxima. |
A time window around the last solar cycle (24th) maxima was chosen, which is composed of sets between 2011 and 2014. Figure 4 shows those data sets and what purpose each one was used for: to train and validate or test the recurrent network models.
At least two data sets were used in all experiments: a continuous or merged data set split randomly into training and validation sets and another set separated exclusively for the test step. The networks’ performance was initially analyzed by looking at the validation loss, which uses an unknown set, but which is used during training in the cross-validation process to evaluate whether the weights’ adjustment is going in the direction of the smallest loss but avoiding the over-fitting problem.
4.2 Loss and accuracy metrics and the networks’ hyperparameters
On the task of comparing the networks’ performance, it is important to define some functions used during the training step to calculate the loss in each step or optimize the networks’ fitting process.
The loss function is used to compare the network processed values with the real values desired in the output layer, for each input sample, in each iteration. A frequently used loss function is the mean squared error (MSE), which was chosen to be adopted in this work to measure the LSTM and GRU performance internally during training and validation steps. MSE is given by:
where n is the training set size (or test set size, when used to evaluate the prediction), yi is the real and desired output value for the ith sample, and 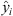 is the network predicted output value for sample i. The decision to use MSE as the loss function resulted from the experiments performed to define the hyperparameters, also explained later in this subsection.
is the network predicted output value for sample i. The decision to use MSE as the loss function resulted from the experiments performed to define the hyperparameters, also explained later in this subsection.
To evaluate the prediction quality, in the test step, we initially chose to compare four different measurements, two of them to measure accuracy (the level of correctness) and the other two to measure the average loss rate in the predictions in which we also included MSE, that was chosen because it punishes the predicted values that are more distant from the real values.
The accuracy measurements were the well-known correlation coefficient (denoted as R) and the coefficient of determination (denoted as R2), which indicates a good fit. R2 is a percentage measure of how well the unseen test samples are likely to be predicted by the model (Pedregosa et al., 2011) used to analyze how much the values of the predicted variable can be dependent on the variation of the real variable; that is, it is used to measure the concordance of the predicted values to the real value. This metric can be estimated as follows:
where 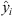 is the predicted value of the ith sample, yi is the corresponding real value, and
is the predicted value of the ith sample, yi is the corresponding real value, and 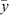 is the real set mean value, given by:
is the real set mean value, given by:
The other loss function, besides the MSE, was the Mean Absolute Percentage Error (MAPE), a forecast model loss measure that provides, through a percentage value, a relative perspective of the test loss. MAPE is given by:
where yi is the real value, and 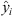 is the predicted value.
is the predicted value.
The other relevant function that had to be chosen for the experiments was the optimizer function, which works with the backpropagation technique in a seek to achieve the minimum loss and the best fitting weights. The basic optimizer technique the backpropagation commonly uses is the gradient descent function, which can be represented in two versions: the one that uses the stochastic gradient descent (SGD) function (Bottou, 2012), and the other that uses the adaptive moment estimation (ADAM) (Kingma & Ba, 2017). The ADAM function is derived from SGD, and the main difference between them is how they treat the learning rate: while SGD uses only a single learning rate for all features present in the chosen data set within a batch, ADAM adapts the learning rate to each feature. Once this work uses forty input features, we concluded that the ADAM optimizer would be the best alternative initially to train the LSTM and GRU networks.
Different values for the hyperparameters were tested to tune the RNNs, keeping fixed only the number of recurrent layers as one in all experiments. The values of the hyperparameters were varied in different combinations until we got a set that provided an acceptable performance. Figure 5 shows one of these experiments regarding the variation of the hidden unit on an LSTM network to TSI 6 h forecast. For this case, the best value of hidden units was 35, but the hidden units optimal value varied among the different networks, in the range of 25–35 units. Despite this variation, we chose to use a unique value of hidden units for all experiments to standardize the hyperparameters and make the comparison between the experiments more meaningful.
 |
Fig. 5 Hidden units number variation in an LSTM experiment for TSI 6 h forecast. |
In the same way that the experiment varying the hidden unit number was carried out, other experiments aimed at tuning the network parameters were performed, such as varying: the batch size, the number of training epochs, and the use of dropout rate, among others. Finally, these experiments contributed to defining the values that gave a better performance to the networks. Table 1 lists the main hyperparameters that were fixed for the experiments that followed, where the Train/Validation ratio represents the split rates used to split the data sets for the training and the validation steps, and the Batch rate refers to the data set percentage used as the batch number.
Hyperparameters used in RNNs.
4.3 LSTM vs. GRU
Initially, the experiments tested the two recurrent architectures – LSTM and GRU – to predict TSI and SSI hours or days ahead. The TSI experiments focused on training LSTM and GRU networks for six hours to three days forecasts (Fig. 6). For each of the six networks, we have done a set of 20 training processes.
 |
Fig. 6 LSTM and GRU Performance Comparison: experiment for 6–72 h TSI forecasts. |
In a similar way to the TSI experiments, the SSI experiments were initially directed to compare both RNNs architectures for one to three days of prediction (Figure 7). Even though the forecasts loss of the three wavelengths were reached at different scales, it can be seen that, as with the TSI experiment, the SSI experiment also shows that the performance of the networks decreases as the forecast interval increases, as would be expected of a forecasting system.
 |
Fig. 7 LSTM and GRU Performance Comparison: experiment for the three wavelengths of SSI, 1–3 days forecasts. |
Those results confirm that the two architectures do not differ significantly in their performance in most cases. Looking at TSI and SSI forecast experiments, the one with 48.5 nm showed that the GRU network, exceptionally, in this case, performed slightly better than LSTM, but still with an intersection between the most extreme results. However, in the other cases, we can see a very similar performance of the two architectures, with LSTM bringing slightly better results than GRU in most of the results.
4.4 TSI prediction
Considering that a single network was trained each time interval of prediction and for each architecture, a total of 30 networks were trained. As there are many results, in this section, we will present only some of them obtained by comparing the real values and the values predicted by the networks.
Figures 8–10 show the TSI 6 h prediction performance obtained from the GRU network. The first one (Fig. 8) presents on the left the training and validation curves reaching the convergence before the first 50 epochs, and on the right, there are the scatter plots of the training and validation sets confronted with the predicted values for them. Figures 9 and 10 show the prediction of the same network for two different test data sets.
 |
Fig. 8 GRU 6 h forecast training and validation performance for TSI. |
 |
Fig. 9 GRU 6 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
 |
Fig. 10 GRU 6 h forecast performance for TSI from 2012/11/20 to 2012/12/18. |
Looking at the results obtained for the TSI forecast 6 h ahead with GRU leads us to believe that they are promising, and the forecast for the two test sets confirms the good forecast quality. The tests for each time interval – 6, 12, 18, 24, 48, and 72 h ahead – were performed using the two recurrent network architectures and for the two test sets. But since both GRU and LSTM showed similar performances, only the results for one of the networks will be presented. The two test sets also showed similar quality results. Therefore, the tests that will be shown are only for the data set from April 25 to July 15, 2013.
Figures 11 and 12 present the TSI forecast for 12 and 18 h ahead. And Figures 13, 14, and 15 present the forecast for the other time intervals: 1, 2, and 3 days.
 |
Fig. 11 LSTM 12 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
 |
Fig. 12 LSTM 18 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
 |
Fig. 13 LSTM 24 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
 |
Fig. 14 LSTM 48 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
 |
Fig. 15 LSTM 72 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
As expected and observed by Vieira et al. (2011a), the quality of the forecasts gets worse as the interval increases. The graphs of the forecasts up to 24 h still present a spread with a pattern closer to those of 6–18 h, while those of two and three days present a lower quality than the other time intervals. The values presented in Table 2 show numerically the quality of these results.
RNNs performance for TSI prediction (mean values), and the same metrics applied to physical models’ (SATIRE and EMPIRE) daily reconstructed values. This performance was obtained for the test period of 2012/11/20 to 2012/12/18.
4.5 SSI prediction
The SSI prediction tests followed the same format as those performed with TSI: the two network architectures were tested, and two sets of tests were used to confirm the prediction quality. The similarity between the two gate architectures was also confirmed in these experiments, and both sets of tests showed similar quality as well. Therefore, only the results for one architecture and one of the test sets will be presented, for the period from December 15, 2012, to April 23, 2013. The prediction was performed one, two, and three days ahead. Initially, Figures 16–18 present the three prediction intervals for 30.5 nm.
 |
Fig. 16 LSTM one day prediction for 30.5 nm from 2012/12/15 to 2013/4/23. |
 |
Fig. 17 LSTM two days prediction for 30.5 nm from 2012/12/15 to 2013/4/23. |
 |
Fig. 18 LSTM three days prediction for 30.5 nm from 2012/12/15 to 2013/4/23. |
For 30.5 nm, the one-day forecast results appear satisfactory, although they did not achieve accuracy similar to TSI’s. Visually, there is only a small deterioration from the one-day to the two-day forecast. The three-day forecast is of poor quality, especially for the smaller irradiance values. The two- and three-day forecasts seem to present a rightward shift.
The predictions for 48.5 nm, presented in Figures 19–21, did not show to be promising for any of the time intervals. This suggests that this wavelength may have a relevant influence on some other specific parameter in its variability. The low irradiance values for this wavelength were the worst predicted values.
 |
Fig. 19 LSTM one day prediction for 48.5 nm from 2012/12/15 to 2013/4/23. |
 |
Fig. 20 LSTM two days prediction for 48.5 nm from 2012/12/15 to 2013/4/23. |
 |
Fig. 21 LSTM three days prediction for 48.5 nm from 2012/12/15 to 2013/4/23. |
Among the three wavelengths, the Lyman-α was the one with the best prediction results, as we can observe through Figures 22–24. Its one-day prediction achieved similar accuracy to the TSI one-day prediction. As for the other wavelengths, the lowest irradiance values of this line showed the worst prediction quality.
 |
Fig. 22 LSTM one days prediction for the spectral line 121.5 nm from 2012/12/15 to 2013/4/23. |
 |
Fig. 23 LSTM two days prediction for the spectral line 121.5 nm from 2012/12/15 to 2013/4/23. |
 |
Fig. 24 LSTM three days prediction for the spectral line 121.5 nm from 2012/12/15 to 2013/4/23. |
 |
Fig. 25 TSI 1 day prediction using GRU vs. physical models reconstructions. |
4.6 RNN prediction and reconstruction with physical models
In the last group of experiments, the RNNs TSI and SSI predictions were compared to the SATIRE (Yeo et al., 2014) and EMPIRE (Yeo et al., 2017) reconstructions. For SSI, only the emission line for Lyman-α was found in the database from where SATIRE and EMPIRE data were downloaded: the Max Planck Institute for Solar System Research7 webpage, so we chose to compare only this emission line results with the physical models.
Although we are making the comparison between the values estimated by physical models and the measurements taken by collection instruments, it is important to make it clear that these series follow their own baselines. Therefore, this comparison is not intended to evaluate the overlap of the physical model curves with those of the measuring instruments (called “real” in this work) or the prediction curves. One of the objectives of this section is to show that the variation of the physical models is much closer to the variation of the “real” values and that neural networks, even if they do not follow this variation exactly, are able to achieve a good prediction accuracy.
In order to display more tangible values obtained as results of the predictions, Tables 2 and 3 show loss and accuracy mean values, over twenty training processes each, obtained for TSI and SSI prediction for the two RNN architectures. The tables also show the same metrics applied to the physical models for the same data period. In the sequence, in Figure 26 and Figure 25, there are two comparative plots from those experiments providing a graphical visualization of the predictions beside the reconstructions.
 |
Fig. 26 Lyman-α 1 day prediction using LSTM vs. physical models reconstructions. |
RNNs performance for SSI prediction (mean loss and mean accuracy), and the same metrics applied to physical models’ (SATIRE and EMPIRE) daily reconstructed Lyman-α values. This performance was obtained for the test period of 2012/12/15 to 2013/4/23.
Looking at Table 2 and doing a joint analysis of performance metrics of the four models, we can see that the RNNs had good performance in short-term forecasts and performed worse as the forecast interval increased, as expected. Analyzing the loss metrics, we notice that the RNNs have smaller values than the physical models. One assumption for this result is that the networks’ predicted values are not so far from the real values even though the correlation is often lower, while even though the physical model curves are well correlated to the real values, sometimes they shift up or down considerably from the real curve. This behavior is ratified by the R2 values, which indicate the quality of the fitting between real values and the estimated ones, showed in Figure 25. R2 values have shown themselves to be considerably higher on RNNs’ predictions when compared to the physical models. Therefore, it can be seen that the prediction results offered by the RNNs for time intervals of up to one day are close to the accuracy offered by the reconstruction models.
Before we analyze the SSI prediction results (in Table 3), it is important to consider that the MSE values can only be compared between the three prediction intervals of the same wavelength since each line varies in a different range. The other metrics follow the same comparison criteria.
The 30.5 nm wavelength results show a reasonable accuracy for the one-day forecast, with MAPE percentage error even slightly lower than those of the physical models, despite representing distinct wavelengths. The two and three days forecasts followed the worsening already expected and observed in all cases when increasing the forecast interval. The other helium line (48.5 nm) showed much lower results for all three intervals.
Since the focus of this work is not the training process improvement for each of the networks individually, the suggestion for future works is an individual training approach for each of the wavelengths. The initial bet could be on varying the hyperparameters and, if necessary, varying the validation and training data sets in an effort to achieve convergence in training, avoiding local minima – a problem also present in some of this work networks’ training – and then obtain better prediction results.
Regarding the Lyman-α results, it was observed that the errors and fitting metrics of our model are very close to those of the physical models and even better than them in the case of the one and two-days forecasts. However, the correlation values are lower than those of the physical models, repeating the profile of other results previously argued. Figure 26 shows the RNNs’ and physical models’ estimations comparison for Lyman-α.
5 Conclusions
Recurrent networks have generally shown themselves to be a good option for predicting total and spectral solar irradiance experiments. The results encourage more specific experiments focusing, for example, on TSI or some specific spectra or short/long-term predictions, depending on the research being conducted.
The main conclusions made during this work were:
None of the two recurrent networks used can be highlighted as presenting better results since the differences between their results were, in general, slight;
As expected, short-term forecasts offered higher accuracy than long-term forecasts. This does not exclude the possibility of good long-term prediction, but this requires adjustments of network hyperparameters and training conditions (training data sets, for instance) which would bring better results for larger prediction intervals;
While correlations with TSI and Lyman-α are equal to or lower than for reconstructions, recurrent networks can offer a very similar estimation accuracy for TSI and Lyman-α forecasts up to one day ahead, with the advantage of predicting these quantities in advance.
It is important to emphasize that in this approach, we chose to perform experiments with the same data sets and hyperparameters for each of the 30 trained networks to compare results, as it was not feasible for this paper to adjust each network individually. However, we believe that more specific experiments with one of the networks, or a subset of them, can bring significant improvements to the results, especially in the cases where the network did not achieve convergence when trained.
5.1 Future work
Numerous possibilities can be derived from this work. Some of them that we can mention are:
This work focused on reproducing the original workflow steps without considering modifications to the original algorithms and their strategies. The first suggestion for future work is an experimental work that focuses on process optimization, starting by analyzing the need of changing, editing, or adding steps to the original version of the workflow.
Since this work dealt with many networks (30 in total), it would be ideal, but it was not feasible to configure each network exclusively. It is then suggested that the network of interest should be improved before using it in a forecast system in order to tune it, configure it with the hyperparameters that offer better performance, and training it to offer a better generalization for the period in which it is desired to be activated, if necessary.
We also suggest taking more varied and larger data periods that cover, for example, different phases of the solar cycle and different cycles. However, for this, it is necessary to treat the existing lack of measured data adequately.
Future works can also consider new strategies to pre-process the input images. One option would be to use another model of solar disk split or another way of weighting sunspots and active regions in different regions of the solar disk by distinguishing, for example, the equatorial region from the polar ones.
Simultaneously, it would be interesting to follow the good data science practices starting with the exploratory data analysis that would precede the forecast and then choosing the more influential input features after knowing, statistically, the relationship between each feature and the observed output value.
To contribute to the reproducibility of this work, the resources – consisting of data, computer codes, notebooks, and other relevant files used in this work – were made available at a Github8 repository of the first author.
Acknowledgments
First of all, the authors thank the editor and anonymous reviewers for their comments and suggestions on this paper. TSI measurements were provided by the LISIRD platform at LASP from SORCE Total Solar Irradiance – Six Hour Average database (https://lasp.colorado.edu/lisird/data/sorce_tsi_6hr_l3/). SSI measurements were also provided by LISIRD from SORCE/SOLSTICE database (https://lasp.colorado.edu/lisird/data/sorce_ssi_l3/) and SDO/EVE database (https://lasp.colorado.edu/lisird/data/sdo_eve_ssi_1nm_l3/), and SDO images were courtesy of NASA/SDO (http://jsoc.stanford.edu/data/hmi/images/). SATIRE and EMPIRE irradiance models data were provided by the Sun-climate group at MPS (https://www2.mps.mpg.de/projects/sun-climate/data.html). This work was financed in part by the Coordenagao de Aperfeigoamento de Pessoal de Nivel Superior – Brasil (CAPES) – Finance Code 001 – CAPES/ME [Grant 88887.504312/2020-00]. This work was also supported in part by the This work was also supported in part by the Conselho National de Desenvolvimento Cientifico e Tecnologico (CNPq) – CNPq/MCTIC [Grant 307404/2016-1] and by the Agenda Espacial Brasileira (AEB) – TED-004/2020-AEB/TO-20VB.0009. The editor thanks two anonymous reviewers for their assistance in evaluating this paper.
SDO webpage: https://sdo.gsfc.nasa.gov/mission/, accessed on April 2021.
SORCE webpage: http://lasp.colorado.edu/home/sorce/, accessed on April 2021.
JSOC webpage: http://jsoc.stanford.edu/data/hmi/images/, accessed on April 2021.
LISIRD webpage: https://lasp.colorado.edu/lisird/, accessed on April 2021.
Max Planck Institute webpage: http://www2.mps.mpg.de/projects/sun-climate/data.html, accessed on April 2021.
References
- Aarts A, Anderson J, Anderson C, Attridge P, Attwood A, et al. 2015. Estimating the reproducibility of psychological science. Science 349(6251): aac4716. Open Science Colaboration, https://doi.org/10.1126/science.aac4716. [CrossRef] [Google Scholar]
- Ball WT, Krivova NA, Unruh YC, Haigh JD, Solanki SK. 2014. A new SATIRE-S spectral solar irradiance reconstruction for solar cycles 21–23 and its implications for stratospheric ozone. J Atmos Sci 71(11): 4086–4101. https://doi.org/10.1175/JAS-D-13-0241.1. [CrossRef] [Google Scholar]
- Ball WT, Unruh YC, Krivova NA, Solanki S, Harder JW. 2011. Solar irradiance variability: A six-year comparison between SORCE observations and the SATIRE model. Astron Astrophys 530: A71. https://doi.org/10.1051/0004-6361/201016189. [CrossRef] [EDP Sciences] [Google Scholar]
- Bottou L. 2012. Stochastic gradient descent tricks. In: Neural Networks: Tricks of the Trade. Montavon G, Orr GB, Müller KR (Eds.) Springer, Berlin, Heidelberg, pp. 421–436. https://doi.org/10.1007/978-3-642-35289-8_25. [CrossRef] [Google Scholar]
- Chauvin Y, Rumelhart DE. 1995. Backpropagation: theory, architectures, and applications. Psychology Press. ISBN 0805812598, 9780805812596. [Google Scholar]
- Cho K, van Merriënboer B, Gulcehre C, Bahdanau D, Bougares F, Schwenk H, Bengio Y. 2014. Learning phrase representations using RNN Encoder–Decoder for Statistical Machine Translation. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP). Association for Computational Linguistics, Doha, Qatar, pp. 1724–1734. https://doi.org/10.3115/v1/D14-1179. [CrossRef] [Google Scholar]
- DeLand MT, Kopp G, Considine DB. 2019. Overview of the NASA Solar Irradiance Science Team (SIST) program special section. Earth Space Sci 6(12): 2229–2231. https://doi.org/10.1029/2019EA000773. [CrossRef] [Google Scholar]
- Ermolli I, Matthes K, Dudok de Wit T, Krivova NA, Tourpali K, et al. 2013. Recent variability of the solar spectral irradiance and its impact on climate modelling. Atmos Chem Phys 13(8): 3945–3977. https://doi.org/10.5194/ACP-13-3945-2013. [CrossRef] [Google Scholar]
- Fidler F, Wilcox J. 2021. Reproducibility of scientific results. In: The Stanford Encyclopedia of Philosophy. Zalta EN (Ed.) Metaphysics Research Lab, Stanford University. https://plato.stanford.edu/archives/sum2021/entries/scientific-reproducibility/. [Google Scholar]
- Fligge M, Solanki S, Unruh Y, Fröhlich C, Wehrli C. 1998. A model of solar total and spectral irradiance variations. Astron Astrophys 335: 709–718. [Google Scholar]
- Fontenla J, Harder J, Livingston W, Snow M, Woods T. 2011. High-resolution solar spectral irradiance from extreme ultraviolet to far infrared. J Geophys Res Atmos 116(D20): 1–31. https://doi.org/10.1029/2011JD016032. [CrossRef] [Google Scholar]
- Fröhlich C, Andersen BN, Appourchaux T, Berthomieu G, Crommelynck DA, et al. 1997. First results from VIRGO, the experiment for helioseismology and solar irradiance monitoring on SOHO. The First Results from SOHO. Springer, pp. 1–25. https://doi.org/10.1007/978-94-011-5236-5_1. [Google Scholar]
- Goodfellow I, Bengio Y, Courville A. 2016. Deep Learning. MIT Press. ISBN 0262337371, 9780262337373. http://www.deeplearningbook.org. [Google Scholar]
- Gray LJ, Beer J, Geller M, Haigh JD, Lockwood M, et al. 2010. Solar influences on climate. Rev Geophys 48(4): 1–53. https://doi.org/10.1029/2009RG000282. [Google Scholar]
- Gulli A, Pal S. 2017. Deep learning with Keras. Packt Publishing Ltd. ISBN 9781787128422. [Google Scholar]
- Haigh JD. 2007. The Sun and the Earth’s climate. Living Rev Sol Phys 4(1): 1–64. https://doi.org/10.12942/lrsp-2007-2. [CrossRef] [Google Scholar]
- Herrera VV, Mendoza B, Herrera GV. 2015. Reconstruction and prediction of the total solar irradiance: From the Medieval Warm Period to the 21st century. New Astron 34: 221–233. https://doi.org/10.1016/j.newast.2014.07.009. [CrossRef] [Google Scholar]
- Hickey JR, Alton BM, Kyle HL, Hoyt D. 1988. Total solar irradiance measurements by ERB/Nimbus-7. A review of nine years. Space Sci Rev 48(3): 321–334. https://doi.org/10.1007/BF00226011. [CrossRef] [Google Scholar]
- Hochreiter S. 1998. The vanishing gradient problem during learning recurrent neural nets and problem solutions. Int J Uncertain Fuzziness Knowlege-Based Syst 6(02): 107–116. https://doi.org/10.1142/S0218488598000094. [CrossRef] [Google Scholar]
- Hochreiter S, Schmidhuber J. 1997. Long short-term memory. Neural Comput 9(8): 1735–1780. https://doi.org/10.1162/neco.1997.9.8.1735. [Google Scholar]
- Jozefowicz R, Zaremba W, Sutskever I. 2015. An empirical exploration of recurrent network architectures. In: Proceedings of the 32nd International Conference on Machine Learning, vol. 37 of Proceedings of Machine Learning Research. Bach F, Blei D, (Eds.). PMLR, Lille, France, pp. 2342–2350. https://proceedings.mlr.press/v37/jozefowicz15.html. [Google Scholar]
- Kingma DP, Ba J. 2017. Adam: a method for stochastic optimization. In: 3rd International Conference for Learning Representations, San Diego, 2015. https://doi.org/10.48550/arXiv.1412.6980. [Google Scholar]
- Kopp G. 2016. Magnitudes and timescales of total solar irradiance variability. J Space Weather Space Clim 6: A30. https://doi.org/10.1051/swsc/2016025. [CrossRef] [EDP Sciences] [Google Scholar]
- Kren AC, Pilewskie P, Coddington O. 2017. Where does Earth’s atmosphere get its energy? J Space Weather Space Clim 7: A10. https://doi.org/10.1051/swsc/2017007. [CrossRef] [EDP Sciences] [Google Scholar]
- Krivova N, Vieira L, Solanki S. 2010. Reconstruction of solar spectral irradiance since the Maunder minimum. J Geophys Res Space Phys 115 (A12): 1–11. https://doi.org/10.1029/2010JA015431. [Google Scholar]
- Li Q, Brown JB, Huang H, Bickel PJ, et al. 2011. Measuring reproducibility of high-throughput experiments. Ann Appl Stat 5(3): 1752–1779. https://doi.org/10.1214/11-AOAS466. [Google Scholar]
- Matthes K, Funke B, Andersson ME, Barnard L, Beer J, et al. 2017. Solar forcing for CMIP6 (v3. 2). Geosci Model Dev 10(6): 2247–2302. https://doi.org/10.5194/gmd-10-2247-2017. [CrossRef] [Google Scholar]
- McNutt M. 2014. Reproducibility. Science 343 (6168): 229. https://doi.org/10.1126/science.1250475. [CrossRef] [Google Scholar]
- Muralikrishna A, Vieira LE, dos Santos RD, Almeida AP. 2020. Total solar irradiance forecasting with keras recurrent neural networks. In: International Conference on Computational Science and Its Applications. Springer, pp. 255–269. https://doi.org/10.1007/978-3-030-58814-4_18. [Google Scholar]
- Nogueira P, Souza J, Abdu MA, Paes R, Sousasantos J, et al. 2015. Modeling the equatorial and low-latitude ionospheric response to an intense X-class solar flare. J Geophys Res Space Phys 120(4): 3021–3032. https://doi.org/10.1002/2014JA020823. [CrossRef] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, et al. 2011. Scikit-learn: Machine learning in Python. J Mach Learn Res 12: 2825–2830. https://www.jmlr.org/papers/volume12/pedregosa11a/pedregosa11a.pdf. [Google Scholar]
- Pinheiro CAO, Senna VD. 2017. Multivariate analysis and neural networks application to price forecasting in the Brazilian agricultural market. Ciência Rural 47(1):1–7. https://doi.org/10.1590/0103-8478cr20160077. [Google Scholar]
- Raulin J, Trottet G, Kretzschmar M, Macotela EL, Pacini A, Bertoni FCP, Dammasch IE. 2013. Response of the low ionosphere to X-ray and Lyman-α solar flare emissions. J Geophys Res Space Phys 118(1): 570–575. https://doi.org/10.1029/2012JA017916. [CrossRef] [Google Scholar]
- Rottman GJ, Woods TN, Sparn TP. 1993. Solar-stellar irradiance comparison experiment 1: 1. Instrument design and operation. J Geophys Res Atmos 98(D6): 10667–10677. https://doi.org/10.1029/93JD00462. [CrossRef] [Google Scholar]
- Rougier NP, Hinsen K, Alexandre F, Arildsen T, Barba LA, et al. 2017. Sustainable computational science: the ReScience initiative. PeerJ Comput Sci 3: e142. https://doi.org/10.7717/peerj-cs.142. [CrossRef] [Google Scholar]
- Solanki SK, Krivova NA, Haigh JD. 2013. Solar irradiance variability and climate. Annu Rev Astron Astrophys 51: 311–351. https://doi.org/10.1146/annurev-astro-082812-141007. [CrossRef] [Google Scholar]
- Stein RF. 2012. Solar surface magneto-convection. Living Rev Sol Phys 9(1): 1–51. https://doi.org/10.12942/lrsp-2012-4. [CrossRef] [Google Scholar]
- Steinhilber F, Beer J, Fröhlich C. 2009. Total solar irradiance during the Holocene. Geophys Res Lett 36(19): 1–5. https://doi.org/10.1029/2009GL040142. [CrossRef] [Google Scholar]
- Tobiska WK, Bouwer SD. 2006. New developments in SOLAR2000 for space research and operations. Adv Space Res 37(2): 347–358. https://doi.org/10.1016/j.asr.2005.08.015. [CrossRef] [Google Scholar]
- Tobiska WK, Woods T, Eparvier F, Viereck R, Floyd L, Bouwer D, Rottman G, White O. 2000. The SOLAR2000 empirical solar irradiance model and forecast tool. J Atmos Sol Terr Phys 62(14): 1233–1250. https://doi.org/10.1016/S1364-6826(00)00070-5. [CrossRef] [Google Scholar]
- Vieira LEA, de Wit TD, Kretzschmar M. 2011a. Short-term forecast of the total and spectral solar irradiance. arXiv. https://doi.org/10.48550/arxiv.1111.5308. https://arxiv.org/abs/1111.5308. [Google Scholar]
- Vieira LEA, Solanki SK, Krivova NA, Usoskin I. 2011b. Evolution of the solar irradiance during the Holocene. Astron Astrophys 531: A6. https://doi.org/10.1051/0004-6361/201015843. [CrossRef] [EDP Sciences] [Google Scholar]
- Willson RC, Gulkis S, Janssen M, Hudson H, Chapman G. 1981. Observations of solar irradiance variability. Science 211(4483): 700–702. https://doi.org/10.1126/science.211.4483.700. [CrossRef] [Google Scholar]
- Wu C-J, Krivova NA, Solanki SK, Usoskin I. 2018. Solar total and spectral irradiance reconstruction over the last 9000 years. Astron Astrophys 620: A120. https://doi.org/10.1051/0004-6361/201832956. [CrossRef] [EDP Sciences] [Google Scholar]
- Yeo K, Krivova N, Solanki S. 2017. EMPIRE: A robust empirical reconstruction of solar irradiance variability. J Geophys Res Space Phys 122(4): 3888–3914. https://doi.org/10.1002/2016JA023733. [CrossRef] [Google Scholar]
- Yeo K, Krivova N, Solanki S, Glassmeier K. 2014. Reconstruction of total and spectral solar irradiance from 1974 to 2013 based on KPVT, SoHO/MDI, and SDO/HMI observations. Astron Astrophys 570: A85. https://doi.org/10.1051/0004-6361/201423628. [CrossRef] [EDP Sciences] [Google Scholar]
Cite this article as: Muralikrishna A, dos Santos RDC & Vieira LEA 2022. Exploring possibilities for solar irradiance prediction from solar photosphere images using recurrent neural networks. J. Space Weather Space Clim. 12, 19. https://doi.org/10.1051/swsc/2022015.
All Tables
RNNs performance for TSI prediction (mean values), and the same metrics applied to physical models’ (SATIRE and EMPIRE) daily reconstructed values. This performance was obtained for the test period of 2012/11/20 to 2012/12/18.
RNNs performance for SSI prediction (mean loss and mean accuracy), and the same metrics applied to physical models’ (SATIRE and EMPIRE) daily reconstructed Lyman-α values. This performance was obtained for the test period of 2012/12/15 to 2013/4/23.
All Figures
 |
Fig. 1 Top: continuum image with sunspots (a), and magnetogram with active regions (b), both registered at the same time (6:00 AM) on 9 November 2011 by HMI/SDO. Bottom: results of running the workflow initial step on the images shown at the top, with umbra and penumbra regions (c) and active regions with different dimensions (d) identified. |
| In the text | |
 |
Fig. 2 Workflow for processing the solar images and predicting solar irradiance. |
| In the text | |
 |
Fig. 3 Part of the training data set: amount of pixels for active regions, umbra and penumbra, TSI and SSI variation, measured in November and December 2011. |
| In the text | |
 |
Fig. 4 Data intervals used for the RNNs training, validation and test steps, considering the period near the 24th solar cycle maxima. |
| In the text | |
 |
Fig. 5 Hidden units number variation in an LSTM experiment for TSI 6 h forecast. |
| In the text | |
 |
Fig. 6 LSTM and GRU Performance Comparison: experiment for 6–72 h TSI forecasts. |
| In the text | |
 |
Fig. 7 LSTM and GRU Performance Comparison: experiment for the three wavelengths of SSI, 1–3 days forecasts. |
| In the text | |
 |
Fig. 8 GRU 6 h forecast training and validation performance for TSI. |
| In the text | |
 |
Fig. 9 GRU 6 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
| In the text | |
 |
Fig. 10 GRU 6 h forecast performance for TSI from 2012/11/20 to 2012/12/18. |
| In the text | |
 |
Fig. 11 LSTM 12 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
| In the text | |
 |
Fig. 12 LSTM 18 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
| In the text | |
 |
Fig. 13 LSTM 24 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
| In the text | |
 |
Fig. 14 LSTM 48 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
| In the text | |
 |
Fig. 15 LSTM 72 h forecast performance for TSI from 2013/4/25 to 2013/7/15. |
| In the text | |
 |
Fig. 16 LSTM one day prediction for 30.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 17 LSTM two days prediction for 30.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 18 LSTM three days prediction for 30.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 19 LSTM one day prediction for 48.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 20 LSTM two days prediction for 48.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 21 LSTM three days prediction for 48.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 22 LSTM one days prediction for the spectral line 121.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 23 LSTM two days prediction for the spectral line 121.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 24 LSTM three days prediction for the spectral line 121.5 nm from 2012/12/15 to 2013/4/23. |
| In the text | |
 |
Fig. 25 TSI 1 day prediction using GRU vs. physical models reconstructions. |
| In the text | |
 |
Fig. 26 Lyman-α 1 day prediction using LSTM vs. physical models reconstructions. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.