| Issue |
J. Space Weather Space Clim.
Volume 14, 2024
Topical Issue - Space Climate: Long-term effects of solar variability on the Earth’s environment
|
|
|---|---|---|
| Article Number | 31 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/swsc/2024031 | |
| Published online | 13 November 2024 | |
Research Article
Association of the 11-year solar cycle with correlation and teleconnection structures in tropospheric circulation
1
Institute of Atmospheric Physics, The Czech Academy of Sciences, Boční II 1401a, 141 00 Prague, Czechia
2
Department of Physical Geography and Geoecology, Faculty of Science, Charles University, Albertov 6, 128 43 Prague 2, Czechia
* Corresponding author: huth@ufa.cas.cz
Received:
30
August
2023
Accepted:
18
September
2024
Analyzing spatial correlation structures and teleconnections in the 500 hPa heights of the Northern Hemisphere Extratropics in winter shows substantial differences between months with high and low solar activity. Patterns of spatial correlations of mid-tropospheric circulation differ between solar minima and maxima; the differences are geographically variable, particularly large and statistically significant in parts of the North Atlantic and North Pacific. Correlation structures of tropospheric circulation are significantly larger in solar maxima over parts of the North Atlantic. The geographical orientation of teleconnections is also associated with solar activity, the differences being most notable over the North Atlantic, North America, and the Arctic. The differences in teleconnections form a background for a response of modes of circulation variability and blocking anticyclones to solar activity, detected in previous studies. We detected no evidence of potential interference of responses to solar activity with quasi-biennial oscillation and volcanic eruptions; the interference with El Niño-Southern Oscillation is unlikely. The response to solar activity may be partly confused with the response to major sudden stratospheric warmings; however, sudden stratospheric warmings themselves may respond to the solar cycle.
Key words: Tropospheric circulation / Solar cycle / Teleconnections / Spatial autocorrelation / Sudden stratospheric warmings
© R. Huth & J. Stryhal, Published by EDP Sciences 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
There is increasing evidence that variations of radiation coming from the Sun, particularly those related to the 11-year solar cycle, affect the troposphere. At least two mechanisms are effective in transferring and amplifying the solar signal into the troposphere: The top-down one consists of downward propagating modifications of the stratospheric polar vortex by additional heating due to enhanced absorption of ultraviolet radiation by stratospheric ozone (Gray et al., 2010). The bottom-up mechanism is based on changes in tropical circulations stemming from enhanced heating of tropical oceans under high solar activity, which propagates poleward (Meehl et al., 2008, 2009).
Several effects of the variability in solar input, related to the 11-year solar cycle, on tropospheric circulation in the Northern Hemisphere Extratropics in winter have been revealed. Many observational studies agree that high solar activity is accompanied by enhanced zonality of circulation, particularly over the North Atlantic and Europe. This is manifested, among others, in composites of mid-tropospheric circulation (Woollings et al., 2010; Brugnara et al., 2013; Sfică et al., 2015; Kuroda et al., 2022), correlation and regression fields (van Loon & Labitzke, 1988; Roy & Haigh, 2011; Gray et al., 2013; Hood et al., 2013; Chen et al., 2015; Maliniemi et al., 2019), a more zonal shape of modes of low-frequency variability and a tendency for the zonally shaped modes to be stronger (Huth et al., 2006, 2007), a more frequent occurrence of zonal circulation types (Huth et al., 2008; Schwander et al., 2017), and a shorter lifetime of blocking events (Barriopedro et al., 2008).
However, there is still some controversy about whether the detected associations between solar variability and tropospheric circulation are real. For example, Chiodo et al. (2019) find correlations between the 11-year solar cycle with the amplitude of the North Atlantic Oscillation (NAO) insignificant and Laken & Stordal (2016) do not find a significant response of wind direction in Central Europe to maxima of the solar cycle. Spiegl et al. (2023) fail to find a response to the solar cycle in an ensemble of simulations by a GCM.
A part of the controversy stems from the fact that a response to a different forcing may be mistaken for the association with solar activity. Such forcings may be either external to the climate system, such as volcanic eruptions, or constitute internal parts of the climate system, most notable examples being quasi-biennial oscillation (QBO), El Niño-Southern Oscillation (ENSO), and major sudden stratospheric warmings (SSWs).
In addition to the associations of the solar cycle with tropospheric circulation, summarized above, several studies indicate that characteristic spatial scales of tropospheric circulation are larger under high solar activity. The first to notice this was Kodera (2002, 2003) for NAO in sea level pressure; his observation has, however, not been elaborated in more detail or generalized in subsequent studies. A larger size under solar maxima is also observed for the action centres of most modes of low-frequency circulation variability (Huth et al., 2006, 2007) and for atmospheric blocking events (Barriopedro et al., 2008), these studies mentioning this fact in the passing only, however, without focusing on them.
This means that the tendency toward a larger size of tropospheric circulation in solar maxima has not been explored systematically until today; it constitutes, therefore, the subject of this paper. We investigate whether and where the spatial scales of tropospheric circulation in the Northern Extratropics and its spatial covariance structures change in association with solar activity. To this end, we make use of the concept of teleconnections, introduced and analyzed in detail by Wallace & Gutzler (1981). Teleconnections are structures of highly correlated (whether negatively or positively) values of a meteorological variable (typically sea level pressure or geopotential heights) over distant areas. We examine the spatial scale of tropospheric circulation by studying several characteristics of correlation and teleconnection structures in the 500 hPa height field. These characteristics are compared between periods of high and low solar activity, considering additional forcings (volcanic eruptions, QBO, ENSO, and SSWs) as potential confounding factors. The analysis is conducted for extended boreal winter months (December to March) because it is during this period that the effects of solar activity on the troposphere have primarily been detected and the top-down mechanism is effective.
2 Data
The analysis is based on sunspot numbers as a measure of solar activity and 500 hPa heights north of 20°N (inclusive) as a characteristic of mid-tropospheric circulation. Solar activity data are monthly mean total sunspot numbers, version 2.0, from the World Data Center, Sunspot Index and Long-term Solar Observations (WDC-SILSO), Royal Observatory of Belgium.1 The source of 500 hPa height data is the NCEP/NCAR reanalysis2 (Kalnay et al., 1996). The horizontal resolution of the reanalysis data is 2.5° in both latitude and longitude. The analysis is carried out for extended winter months (December to March) for the period from January 1948 to December 2022, which amounts to 300 months (75 years times 4 months each year) altogether. For the sake of comparison, we also use the most recent reanalysis, ERA53 (Hersbach et al., 2020), downsampled from its native 0.25° resolution to the same horizontal resolution by simply taking every tenth gridpoint in both directions. Unless otherwise stated, all results are presented for NCEP/NCAR only. Both reanalyses are compared in Section 3.6.
We also utilize information on major sudden stratospheric warmings (SSWs), quasi-biennial oscillation (QBO), volcanic eruptions, and El Niño/Southern Oscillation (ENSO). We make use of the updated and complemented list of SSWs from Siddiqui et al. (2018).4 We consider the month when an SSW occurred and the following month as affected by an SSW; the months before an SSW and the winters without any SSW are considered as not affected by SSWs. Years before 1958 when we had no data on SSWs are excluded from considerations regarding SSWs. Equally so are excluded the second and third months after a SSW since it is not clear a priori whether the polar vortex recovered. The phase of QBO is defined by the sign of the mean monthly 40 hPa equatorial wind as provided by the Free University of Berlin.5 The time series starts in March 1953 and ends in November 2021; the months outside the time range are excluded from analyses related to QBO. Further, we consider the year with a major volcanic eruption with a dust veil index of five and larger and the year following it as affected by the eruption. The timing and intensity of volcanic eruptions are taken from the Global Volcanic Program of the Smithsonian Institution.6 ENSO is quantified by the Niño3.4 index7 (Rayner et al., 2003, updated). We define El Niño/La Niña months as those with the positive/negative standardized Niño3.4 index.
Separate analyses are conducted for months with low and high solar activity. Low and high solar activity is defined by quartiles of the sunspot number, that is, individual months with sunspot numbers in the lower 25% of its distribution are identified with low solar activity and individual months with sunspot numbers in its upper 25% are identified with a high solar activity. Results are not sensitive to the exact definition of low and high solar activity or to whether the assignment to high and low solar activity is done for individual months (as here) or seasons as a whole. Nevertheless, less extreme definitions than those used here (e.g., using terciles instead of quartiles to define the solar cycle phases) tend to yield a weaker association between solar activity and atmospheric circulation. We use the terms ‘low solar activity’ and ‘solar minimum’ (and equivalently ‘high solar activity’ and ‘solar maximum’) interchangeably.
Statistical significance is assessed by Monte Carlo (resampling) approach; for its description and a few relevant examples of its application see Livezey & Chen (1983), Vautard et al. (1990), Wilks (2006), Laken & Čalogović (2013), or Schwander et al. (2017). It consists here of creating 500 random series, obtained by re-shuffling the monthly circulation data and assigning the re-shuffled series to the original unchanged sunspot time series. We conduct resampling of four-month (winter) blocks, that is, the months from individual winters (December of one year to March of the next year) are kept together in resampled data. For the sake of consistency, January to March 1948 is kept together with December 2022 in the resampling procedure. This procedure accounts both for the temporal structure of the sunspot data, including their temporal autocorrelation, and for the temporal autocorrelation in 500 hPa data, which is nonnegligible for consecutive months, while generally negligible between consecutive years. Finally, the tested characteristic calculated from real data is compared with the ordered tested characteristic for the 500 re-shuffled datasets, thus determining the statistical significance. We claim the observed characteristic to be statistically significant at the 5% level for a two-tailed test if it falls within the lower 2.5% or upper 2.5% of the re-shuffled characteristics, that is, is smaller than the 13th re-shuffled value or larger than the 487th re-shuffled value.
3 Results
3.1 One-point correlation maps
We start with spatial correlation structures. They are characterized by one-point correlation maps, which display correlations of time series between the reference point and all other grid points. Figure 1 provides examples of such one-point correlation maps with contrasting behaviour relative to phases of the solar cycle. Correlations with points 37.5°N/70°W and 25°N/170°E (top two rows) exhibit little differences between solar minima (left) and maxima (right). For the former, positive correlations extend in a belt leading eastward up to eastern Europe and westward across the Pacific, the negative centre being confined to northern North America and the North Atlantic, with a slight sign of extension towards north of the Bering Strait in solar maxima. For the latter, the positive centre extends along most of the subtropics with an interruption over the central Atlantic in both phases of the solar cycle, while the negative centre resides over the Aleutian Islands, although it extends more westwards in solar maximum. Correlations for two other points, 60°N/90°W and 47.5°N/132.5°W (bottom two rows of Fig. 1) provide a contrasting case in which correlation patterns strongly differ between the two solar phases. For the former, all the major centres are more spatially extensive in solar maxima, especially in the zonal direction. Negative correlations occupy a belt from the western coast of North America to central Europe, which is very different from solar minima when they are confined to eastern North America and a small adjacent part of the Atlantic. The latter example is characterized by a northward extension of its positive centre and two negative centres at its eastern and western flanks in solar minima; in solar maxima, these features are almost missing, whereas areas with positive correlations emerge over the Caribbean and South Asia.
 |
Figure 1 One-point correlation maps for four points (in rows) for low (left) and high (right) solar activity. The geographical coordinates of the points are provided together with the congruence coefficient (multiplied by 100) between the two maps. Contour interval is 0.2, negative contours are dashed, zero contour is omitted. Negative values below −0.3, which are later used for the definition of teleconnected area, are shaded. Red dot indicates the base point; red cross indicates the point with most negative correlation, used for the definition of teleconnectivity. |
These examples demonstrate that spatial correlation structures are related to solar activity, and this relation is geographically dependent: there are regions for which the differences in one-point correlation maps between high and low solar activity are large, whereas in other regions they are rather small. A more detailed insight into the relation of correlation structures to solar activity is provided by quantifying the similarity of one-point correlation maps between the solar cycle phases. For this purpose, the coefficient of congruence (i.e., uncentered correlation) is calculated, which is more suitable for measuring the similarity of two fields than the correlation coefficient if not only the pattern but also the magnitude is relevant (Richman & Lamb, 1985). The congruence coefficient attains the same range of values as the correlation coefficient (from −1, indicating a perfect negative relationship, through zero, indicating no relationship, to +1, indicating a perfect positive relationship) with a tendency for its values to be larger (in absolute sense).
The values of congruence between the one-point correlation maps in solar minimum and solar maximum are displayed in Figure 2. They exceed 0.8 (grey shading in Fig. 2) over the majority of the Northern Hemisphere Extratropics, including lower latitudes over Eurasia and the western Pacific, the Arctic, and the area along the core of the North Atlantic storm track. Low values indicate a dissimilarity of one-point correlation maps between the solar cycle phases, that is, suggest a strong association of spatial correlation structures with the solar cycle. The low values are observed in the neighbourhood of the major storm tracks: north of the Pacific storm track and at its exit near the North American coast, and both north and south of the Atlantic storm track (cf. Fig. 1a in Hoskins & Hodges, 2019). The highest dissimilarity of one-point correlation maps between the solar cycle phases is found west of the northwestern U.S.; the congruence coefficient falls below 0.4 there.
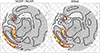 |
Figure 2 Congruence coefficient between one-point correlation maps for solar minimum and solar maximum multiplied by 100: black contours, contour interval 10, areas with values exceeding 80 shaded. Grid points where the correlation maps for solar maximum and solar minimum are not identical at the 10%, 5%, and 1% significance levels (i.e., are dissimilar enough) are shown in turn by red, orange, and yellow lines. NCEP-NCAR reanalysis (left) and ERA5 reanalysis (right). |
One-point correlation maps can be produced for every grid point. The huge amount of information contained in the large number of such maps is difficult to comprehend, however. In the following text (Sects. 3.2 and 3.3) we introduce and evaluate two characteristics, which aggregate every one-point correlation map into a single number.
3.2 Teleconnectivity
First, we assign to every grid point the absolute value of the most negative correlation in its one-point correlation map; we refer to this characteristic as ‘teleconnectivity’ following Wallace & Gutzler (1981). For example, the teleconnectivity of the grid points discussed above in solar minimum and solar maximum, respectively, is 0.47 and 0.55 for 25°N, 170°E, and 0.48 and 0.34 for 47.5°N, 132.5°W.
The maps of teleconnectivity for solar minima and maxima are displayed in the top row of Figure 3. The patterns in both solar cycle phases are similar: the areas of high teleconnectivity (over 0.6; shaded areas in Fig. 3) concentrate over the eastern North Atlantic, western North America and the central North Pacific. These structures are reminiscent of the two strongest modes of variability (teleconnections) in the Northern Extratropics. The two centres of high teleconnectivity over the North Atlantic constitute the NAO, and the three centres over the Pacific and western North America form a substantial part of the Pacific-North American (PNA) pattern. The pattern of the difference in teleconnectivity between solar maxima and minima is rather scattered; worth noting is that the difference reflects a zonal extension of the southern centre of NAO towards central North America and into the European interior (top right of Fig. 3). However, differences in teleconnectivity between the two solar cycle phases are large enough to achieve statistical significance in small areas only, which are rather patchy. This all indicates that the association between solar activity and teleconnectivity is weak if any.
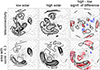 |
Figure 3 Maps for solar minimum (left) and solar maximum (middle) of teleconnectivity multiplied by 100 (top row) and normalized teleconnected area (for more details see text; bottom row). Teleconnectivity: contour interval 10, contours start at 50, values over 60 are shaded. Teleconnected area: contours 100, 200, 300, 400, 600, and 800; light and dark shading for values over 200 and 600, respectively. Differences between solar maximum and solar minimum and their statistical significance (right): differences denoted by black contours, dashed for negative values; for teleconnectivity, contour interval is 20, starting from ±10; for teleconnected area, contour interval is 200, starting from ±100; significance at the 10%, 5%, and 1% levels is denoted in turn by a thick coloured contour, light coloured shading, and dark coloured shading; positive and negative differences are shown in red and blue, respectively. |
3.3 Teleconnected area
Perhaps more intuitive and easier to interpret is the other characteristic we use. For each grid point, we calculate the area with negative correlations below −0.3. The selection of this threshold is somewhat arbitrary; nevertheless, the results regarding associations with the solar cycle are not sensitive to this choice. We approximate the area by the number of gridpoints where the correlation is below the threshold, multiplied by the cosine of the latitude. This is equivalent to the normalization of the area by the size of a grid box at the equator, which is approximately 77,270 km2. We limit ourselves to negative correlations in the calculation of the teleconnection area simply because the highest positive autocorrelations occur in the vicinity of the base point, which is not relevant as we are interested in teleconnections, i.e., correlations over large distances.
The maps of the teleconnected area (Fig. 3 bottom) show particularly high values between 40° and 50° N over the North Atlantic and Western Europe. The values are much higher there and the area of high values is considerably more extensive in solar maxima: much larger areas are highly correlated with points in this belt in solar maxima than in solar minima. The belt of high values of teleconnected area in solar maxima extends from central North America up to central Europe. The entire structure of high values in the Euro-Atlantic sector as well as their large differences is reminiscent of NAO, including the centre over southern Greenland and the belt over western to central Sahara in solar maxima. Teleconnected area is also larger in solar maxima over the western to central North Pacific. Another smaller belt with high values of teleconnected area is located along 50°N in East Asia.
The differences in the teleconnected area are more substantial than those in teleconnectivity. Almost all significant differences are positive (Fig. 3 bottom right): wherever the teleconnected area significantly differs between the solar cycle phases, it is larger in solar maxima.
3.4 Orientation of teleconnections
Finally, we look at the location and orientation of strong teleconnections. For this purpose, a map is displayed (Fig. 4) in which each grid point is connected by a straight line with the grid point with which it has the most negative correlation provided the correlation in absolute value is at least 0.45. The strength of the correlation is coded by colour, ranging from yellow for correlations between 0.45 and 0.50 through red to dark blue (for correlations over 0.70). Most lines (that is, strong negative correlations) are oriented in a meridional direction across major storm tracks. The strength and direction of strong correlations are similar between the solar cycle phases over the North Pacific: we can see mostly meridional connections, with some zonal connections of the central North Pacific with the western U.S. coast (which can be attributed to PNA), all tending to be somewhat stronger in solar maxima. Correlations of central Siberia and northern China with the Arctic and Scandinavia are much stronger in solar minima. Some correlations over 0.45 are limited to one solar cycle phase: those across North America along the U.S.-Canadian border only occur in solar minima, whereas those between the southeastern U.S. and North Atlantic, and between northern Africa and easternmost Atlantic/southwestern Europe only occur in solar maxima. The connection of the area west of the Ural Mountains with western Europe and the northernmost Atlantic is much stronger in solar maxima as well.
 |
Figure 4 Teleconnection diagram for solar minima (top) and solar maxima (bottom). Each point is connected by a straight line to the point with which it is most strongly negatively correlated. Only correlations (in absolute value) over 0.45 are displayed, colours denoting their strength. |
The largest differences between the solar cycle phases are observed over the North Atlantic sector. In solar maxima, strong correlations are much more widespread there, with the Atlantic area of strong correlations extending farther both westward (up to central Canada and the Gulf of Mexico) and eastward (up to easternmost Europe). Worth noting is a much more zonal orientation of correlations in solar maxima.
Perhaps most notable are the areas where the direction of connections differs between solar minima and maxima. This is mainly the case in the European Arctic: the area between northern Europe and the North Pole is connected to Siberia and Eastern Asia in solar minima but to eastern North Atlantic and southwestern Europe in solar maxima.
The fact that strong negative correlations are more numerous in solar maxima is supported by Table 1, showing the counts of grid points with negative correlations for various ranges of thresholds. Except for the very strong correlations over 0.70, which are quite infrequent, and marginally for the range 0.50 to 0.55, the number of strong correlations is higher for solar maxima.
Numbers of points with negative correlations (in absolute value) in the given range, separately for solar minima and maxima.
3.5 Confounding forcings
A possible coincidence of SSWs, volcanic eruptions, and a particular phase of ENSO and QBO with a particular phase of the solar cycle might lead to a misleading attribution of their effects on solar variability. Table 2 indicates that such a coincidence is an issue for SSW and volcanic eruptions, which both occur disproportionately (relative to a random expectation) more often under solar maxima, whereas both phases of QBO and ENSO are spread quite uniformly under low and high solar activity.
Contingency tables between phases of solar cycle (rows) and occurrence/phase of confounding forcings (columns): each entry displays the respective number of months. The last row provides χ2-statistics; asterisks denote their statistical significance at the 5% level.
In the following, we present maps of congruence coefficients (Fig. 5) and teleconnected area (Fig. 6), analogously to Figures 2 and 3, for the absence and presence of SSWs and volcanic eruptions and two phases of QBO and ENSO. The similarity of one-point correlation maps, as expressed by congruence coefficients, for QBO exceeds 0.8 almost everywhere, without any sign of decreased values over the North Atlantic and easternmost North Pacific. The maps of teleconnected area bear a great deal of similarity between the two QBO phases, although with slightly higher values for the easterly phase in the North Atlantic maximum. This means that the association of the measures of tropospheric circulation with solar activity differs substantially from the effect of QBO. The erratic nature of the congruence field for volcanic eruptions and a rather large area with low values are likely due to a small sample size of months affected by volcanic eruptions. The spatial structure of the congruence field for volcanic eruptions is substantially different from that for solar cycle phases. The same applies to the teleconnected area. Therefore, we conclude that the effects of neither QBO nor volcanic eruptions can be mistakenly attributed to associations with solar activity.
 |
Figure 5 Congruence coefficient between one-point correlation maps for absence and presence of SSW, two phases of QBO, absence and presence of volcanic eruptions, and two phases of El Niño, multiplied by 100: contour interval 10, areas with values exceeding 80 shaded. |
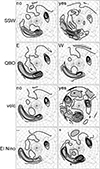 |
Figure 6 Maps of teleconnected area for the absence/presence or two phases of SSW, QBO, volcanic eruptions, and El Niño. Contours 100, 200, 300, 400, 600, and 800; light and dark shading for values over 200 and 600, respectively. |
The teleconnected area is larger under the positive phase of ENSO in the belt over the North Atlantic; however, the difference between the two ENSO phases is substantially smaller than the difference between the solar cycle phases. This, together with the congruence map for El Niño, which exhibits no similarity with its counterpart for solar activity, allows us to claim that ENSO effects are very unlikely to account for the detected associations with the solar cycle.
The congruence of autocorrelation maps between the absence and presence of SSW bears some similarity to the congruence between solar cycle phases, particularly in the southern belt of low values over the North Atlantic and area of low values off the western North American coast. However, considerable discrepancies between the congruence maps for SSW and solar cycle appear for the northern North Atlantic belt and over eastern Asia. While the teleconnected area over the North Atlantic is larger under the presence of an SSW than without it, which concurs with the effect of the solar cycle, the difference is considerably smaller for SSWs than for the solar cycle. Our interpretation is that a minor part of the association of tropospheric circulation with the solar cycle may be accounted for by the presence of SSWs: SSWs can contribute to the association that we have detected or strengthen it. At the same time, the solar cycle may affect the occurrence of SSWs, although the relationship is not robust and is likely to be modulated by the QBO phase (Baldwin et al., 2021). Therefore, the effect that SSWs have on tropospheric circulation may be largely due to solar effects on SSWs themselves.
3.6 ERA5 reanalysis
The above analyses were repeated for the ERA5 reanalysis. Results are presented in Figure 2 right for the congruence of one-point correlation maps between high and low solar activity. They are very similar to the NCEP/NCAR reanalysis (Fig. 2 left). In particular, the areas of low congruence, that is, of largest discrepancies in correlation structures between high and low solar activity, almost coincide between the two reanalyses.
Outputs for ERA5 and NCEP/NCAR are analogously close to each other for other analyses described above and their presentation would, therefore, be redundant. In order to save space, we decided to limit ourselves to presenting results for NCEP/NCAR only.
The high similarity of outputs between the two reanalyses adds confidence to our results in that they are not artefacts of a single specific dataset.
4 Discussion and prospects
The current analysis should be treated as a preliminary study, which points to a specific manifestation of the linkage between solar variability and tropospheric circulation but does not delve into details. The analysis raises several research questions, which we plan to answer in a coming study:
(Non-)stationarity of the association. Several previous studies point to the non-stationarity of solar effects on the troposphere, particularly because observational studies typically rely on a relatively short most recent period (Kuroda et al., 2022; Ma et al., 2018; Maliniemi et al., 2016). To this end, long-term reanalyses going back to the beginning of the 20th century (ERA-20C starting 1900) or even to the first half of the 19th century (20CR, its most recent version starting 1836) may be utilized. These reanalyses, however, only assimilate surface data (pressure, winds, sea surface temperature) to reconstruct the fully three-dimensional structure of the atmosphere; therefore, it is not self-evident that they can reproduce subtle tropospheric responses to the solar cycle. Because of this, the ability of long-term reanalyses to detect solar effects must first be compared with the reanalyses that assimilate all available data (such as NCEP/NCAR and ERA5 used in this study) on a shorter period starting ideally in the middle of the 20th century.
Optimization of lag. Various potential mechanisms of effects of solar variability on the troposphere operate with different time lags. Several studies search for the optimum lag, i.e., the lag for which the particular impact is strongest (Andrews et al., 2015; Mitchell et al., 2015; Kuroda et al., 2022). Depending on the mechanism and variable considered, the optimum lag varies from one month for the response of NAO to strong solar wind events (Boberg & Lundstedt, 2002), through several weeks or months needed for a signal to propagate from the stratosphere downward or due to the memory in snow cover and sea ice (Baldwin & Dunkerton, 2001; Ogi et al., 2003), to several years due to the memory in the ocean (Andrews et al., 2015; Scaife et al., 2013). The analysis presented here assumes an immediate response; this is, however, not at variance with the just mentioned studies thanks to a high temporal autocorrelation of monthly and annual sunspot numbers. Moreover, some studies identify zero lag as optimum (Maliniemi et al., 2013; Liu et al., 2014). Therefore, the identification of the lag for which the response of tropospheric teleconnections to solar cycle maximizes appears to be a relevant research question.
Seasonality. The response of the troposphere to solar forcing has been shown to change during the winter season; especially it differs between early and late winter (Gray et al., 2016; Kuroda et al., 2022; Ma et al., 2018; Maliniemi et al., 2016, 2019; Zhu et al., 2020). Therefore, we also plan to analyze whether the association of teleconnection measures varies during the winter season and whether it persists until summer, similar to the relation between solar cycle and the vertical dimension of NAO studied by Ogi et al. (2003).
A specific mention must be devoted to the role of SSWs. The association of teleconnection measures with the presence of SSWs is similar to that with the solar cycle. Since the response of SSWs to solar cycle is unclear, it is also unclear to what degree, and if at all, SSWs themselves, that is, regardless of their solar forcing, interfere with the associations to the solar cycle. Here, a long-term reanalysis would not help because SSW data are only available starting from 1958. Therefore, the question of the role of SSWs in associations of tropospheric circulation to the solar cycle may only be answered by modelling studies.
There are two possible interpretations and future outcomes of the controversy between the studies confirming and denying solar cycle effects on (not only) tropospheric circulation. First, the denying studies may be right, the positive outcomes in the numerous studies obtained until today being a result of an insufficient size of the sample available and/or an imperfect statistical treatment of data. Contrarily, the truth may be on the side of the confirming studies; in such a case, the explanation of the denying outputs of some studies may consist in too specific or narrow research questions (e.g., looking at the response of NAO amplitude only), the use of techniques unsuitable for the detection of solar effects, or inability of climate models to correctly simulate some processes in the cause-and-effect chain.
A more detailed and complex analysis, answering research questions raised above, will allow one to confirm or deny the realism of associations between solar variability and spatial structure of mid-tropospheric circulation. Only an analysis encompassing various lags and different segments of the winter season will enable hypotheses regarding mechanisms staying behind such associations to be made, even though a fully reliable attribution of observed tropospheric effects to specific causes is possible only through modelling studies.
5 Conclusions
The analysis focuses on differences in the spatial structure of mid-tropospheric circulation between solar minima and maxima, as revealed by the NCEP/NCAR reanalysis dataset. The solar maxima and minima are defined by lower and upper quartiles of the monthly sunspot numbers. Results are not sensitive to the exact definition of maxima and minima. All results are confirmed in the most recent reanalysis, ERA5.
The spatial scale of tropospheric circulation, quantified by the area strongly negatively correlated with a base grid point (which we refer to as ‘teleconnected area’) in the field of 500 hPa heights, is shown to differ between solar maxima and minima. The spatial scale of circulation is larger in solar maxima particularly in the Euro-Atlantic sector. This is congruent with earlier results obtained by different techniques for datasets confined regionally and/or to a few specific teleconnections (Kodera, 2002, 2003; Huth et al., 2006; Barriopedro et al., 2008) and supports results of Huth et al. (2006) that teleconnection patterns in the Euro-Atlantic domain in solar maxima are more spatially extensive. Another measure that we use, the amplitude of the most negative correlation with a base point (‘teleconnectivity’), exhibits a rather limited association with solar cycle phases, although there are hints of increased teleconnectivity over the Atlantic related to the zonal extension of NAO under solar maxima. Changes in both teleconnection measures concentrate in the vicinity of major storm tracks. This, together with the fact that the strength and position of the storm tracks are regulated by the major teleconnection patterns (NAO, PNA), points to the relevance of the changing spatial scale of circulation to processes in synoptic and intraseasonal time scales. For example, the increased spatial scale of teleconnections manifests in atmospheric blocks over the North Atlantic covering larger areas in solar maxima (as reported by Barriopedro et al., 2008). Another consequence of the increased spatial scale of teleconnections is that the area where the individual teleconnections influence surface air temperature and precipitation becomes larger; cf. Hynčica and Huth (2022).
Teleconnections also change their direction between solar minima and maxima in some areas. Specifically, strong one-point correlations are more abundant and tend to be oriented more zonally in the Atlantic domain in solar maxima. This is in line with the increased zonality of teleconnections there and more variance associated with zonally oriented teleconnections in solar maxima, as shown by Huth et al. (2006, 2007). In other words, the Atlantic zonal modes, i.e., NAO and East Atlantic pattern, are stronger, while centres of the meridionally oriented modes, that is, both Eurasian modes, tend to take on more zonal shapes. All these effects result in westerly winds being more prevalent and/or stronger in solar maxima, which is in various ways reported e.g. by Woollings et al. (2010), Ineson et al. (2011), Chen et al. (2015), Schwander et al. (2017), and Maliniemi et al. (2019). A tendency of North America to be more strongly correlated with the Pacific basin in solar minima, whereas with the Atlantic basin in solar maxima, explains the extension of NAO into North America in solar maxima. This is accompanied by a retreat of teleconnections operating in the Pacific sector (PNA) or even their disappearance (Tropical–Northern Hemisphere pattern) (Huth et al., 2006). A consequence of these effects is a stronger influence of NAO on air temperature and precipitation in eastern North America in solar maxima, replaced by a stronger influence of PNA there in solar minima.
We demonstrate that the associations with the solar cycle that we detect are unlikely to be attributed to the effects of volcanic eruptions, QBO, and ENSO. We detect a possible interference of the solar cycle with SSWs.
It appears that it is the changing spatial scale of circulation patterns, quantified here by correlation maps and characteristics derived from them, that forms a background for the reflection of solar activity in the characteristics of extratropical tropospheric circulation, such as modes of variability and blocking events. However, what is the mechanism that causes the atmospheric circulation to change its spatial scale in association with solar activity cannot be determined by an observational study and remains, therefore, unclear. Modelling studies are needed for our understanding of what is behind this phenomenon. It is also modelling studies that only can answer the question on the role of SSWs. More work is also needed to trace the causes of the association between solar activity and spatial structure of tropospheric circulation, assess its stability in time, determine the time lag, in which the association operates most strongly, and analyze its timing within the winter season.
Acknowledgments
The authors wish to thank data providers for making their datasets available: NOAA PSL, Boulder, Colorado, USA; ECMWF, Reading, UK; WDC-SILSO, Royal Observatory of Belgium, Brussels; Free University of Berlin, Germany; and Smithsonian Institution, Washington D.C., USA. The editor thanks two anonymous reviewers for their assistance in evaluating this paper.
References
- Andrews MB, Knight JR, Gray LJ. 2015. A simulated lagged response of the North Atlantic Oscillation to the solar cycle over the period 1960–2009. Environ Res Lett 10: 054022. https://doi.org/10.1088/1748-9326/10/5/054022. [CrossRef] [Google Scholar]
- Baldwin MP, Dunkerton TJ. 2001. Stratospheric harbingers of anomalous weather regimes. Science 294: 581–584. [CrossRef] [Google Scholar]
- Baldwin MP, Ayarzagüena B, Birner T, Butchart N, Butler AH, et al. 2021. Sudden stratospheric warmings. Rev Geophys 59: e2020RG000708. https://doi.org/10.1029/2020RG000708. [CrossRef] [Google Scholar]
- Barriopedro D, García-Herrera R, Huth R. 2008. Solar modulation of Northern Hemisphere winter blocking. J Geophys Res 113: D14118. https://doi.org/10.1029/2005JD006813. [Google Scholar]
- Boberg F, Lundstedt H. 2002. Solar wind variations related to fluctuations of the North Atlantic Oscillation. Geophys Res Lett 29(15): 13. https://doi.org/10.1029/2002GL014903. [CrossRef] [Google Scholar]
- Brugnara Y, Brönnimann S, Luterbacher J, Rozanov E. 2013. Influence of the sunspot cycle on the Northern Hemisphere wintertime circulation from long upper-air data set. Atmos Chem Phys 13: 6275–6288. https://doi.org/10.5194/acp-13-6275-2013. [CrossRef] [Google Scholar]
- Chen HS, Ma HD, Li X, Sun SL. 2015. Solar influences on spatial patterns of Eurasian winter temperature and atmospheric general circulation anomalies. J Geophys Res Atmos 120: 8642–8657. https://doi.org/10.1002/2015JD023415. [CrossRef] [Google Scholar]
- Chiodo G, Oehrlein J, Polvani LM, Fyfe JC, Smith AK. 2019. Insignificant influence of the 11-year solar cycle on the North Atlantic Oscillation. Nat Geosci 12: 94–99. https://doi.org/10.1038/s41561-018-0293-3. [CrossRef] [Google Scholar]
- Gray LJ, Beer J, Geller M, Haigh JD, Lockwood M, et al. 2010. Solar influences on climate. Rev Geophys 48: RG4001. https://doi.org/10.1029/2009RG000282. [Google Scholar]
- Gray LJ, Scaife AA, Mitchell DM, Osprey S, Ineson S, et al. 2013. A lagged response to the 11 year solar cycle in observed winter Atlantic/European weather patterns. J Geophys Res Atmos 118: 13405–13420. https://doi.org/10.1002/2013JD020062. [Google Scholar]
- Gray LJ, Woollings TJ, Andrews M, Knight J. 2016. Eleven-year solar cycle signal in the NAO and Atlantic/European blocking. Quart J Roy Meteorol Soc 142: 1890–1903. https://doi.org/10.1002/qj.2782. [CrossRef] [Google Scholar]
- Hersbach H, Bell B, Berrisford P, Hirahara S, Horányi A, et al. 2020. The ERA5 global reanalysis. Quart J Roy Meteorol Soc 146: 1999–2049. https://doi.org/10.1002/qj.3803. [CrossRef] [Google Scholar]
- Hood L, Schimanke S, Spangehl T, Bal S, Cubasch U. 2013. The surface climate response to 11-year solar forcing during northern winter: observational analyses and comparisons with GCM simulations. J Clim 26: 7489–7506. https://doi.org/10.1175/JCLI-D-12-00843.1. [CrossRef] [Google Scholar]
- Hoskins BJ, Hodges KI. 2019. The annual cycle of Northern Hemisphere storm tracks. Part I: Seasons. J Clim 32: 1743–1760. https://doi.org/10.1175/JCLI-D-17-0870.1. [CrossRef] [Google Scholar]
- Huth R, Pokorná L, Bochníček J, Hejda P. 2006. Solar cycle effects on modes of low-frequency circulation variability. J Geophys Res 111: D22107. https://doi.org/10.1029/2005JD006813. [Google Scholar]
- Huth R, Bochníček J, Hejda P. 2007. The 11-year solar cycle affects the intensity and annularity of the Arctic Oscillation. J Atmos Sol-Terr Phys 69: 1095–1109. https://doi.org/10.1016/j.jastp.2007.03.006. [CrossRef] [Google Scholar]
- Huth R, Kyselý J, Bochníček J, Hejda P. 2008. Solar activity affects the occurrence of synoptic types over Europe. Ann Geophys 26: 1999–2004. https://doi.org/10.5194/angeo-26-1999-2004. [CrossRef] [Google Scholar]
- Hynčica M, Huth R. 2022. Temporal evolution of relationships between temperature and circulation modes in five reanalyses. Int J Climatol 42: 4391–4404. https://doi.org/10.1002/joc.7474. [CrossRef] [Google Scholar]
- Ineson S, Scaife AA, Knight JR, Manners JC, Dunstone NJ, et al. 2011. Solar forcing of winter climate variability in the Northern Hemisphere. Nat Geosci 4: 753–757. https://doi.org/10.1038/NGEO1282. [CrossRef] [Google Scholar]
- Kalnay E, Kanamitsu M, Kistler R, Collins W, Deaven D, et al. 1996. The NCEP-NCAR 40-year reanalysis project. Bull Amer Meteorol Soc 77: 437–471. https://doi.org/10.1175/1520-0477(1996)077<0437:TNYRP>2.0.CO;2. [CrossRef] [Google Scholar]
- Kodera K. 2002. Solar cycle modulation of the North Atlantic Oscillation: implication in the spatial structure of the NAO. Geophys Res Lett 29: 1218. https://doi.org/10.1029/2001GL014557. [CrossRef] [Google Scholar]
- Kodera K. 2003. Solar influence on the spatial structure of the NAO during the winter 1900–1999. Geophys Res Lett 30: 1175. https://doi.org/10.1029/2002GL016584. [Google Scholar]
- Kuroda Y, Kodera K, Yoshida K, Yukimoto S, Gray L. 2022. Influence of the solar cycle on the North Atlantic Oscillation. J Geophys Res Atmos 127: e2021JD035519. https://doi.org/10.1029/2021JD035519. [CrossRef] [Google Scholar]
- Laken BA, Čalogović J. 2013. Composite analysis with Monte Carlo methods: an example with cosmic rays and clouds. J Sp Wea Sp Clim 3: A29. https://doi.org/10.1051/swsc/2013051. [Google Scholar]
- Laken BA, Stordal F. 2016. Are there statistical links between the direction of European weather systems and ENSO, the solar cycle or stratospheric aerosols? Roy Soc Open Sci 3: 150320. https://doi.org/10.1098/rsos.150320. [CrossRef] [Google Scholar]
- Liu ZF, Yoshimura K, Buenning NH, He XG. 2014. Solar cycle modulation of the Pacific-North American teleconnection influence on North American winter climate. Environ Res Lett 9: 024004. https://doi.org/10.1088/1748-9326/9/2/024004. [CrossRef] [Google Scholar]
- Livezey RE, Chen WY. 1983. Statistical field significance and its determination by Monte Carlo techniques. Mon Wea Rev 111: 46–59. [CrossRef] [Google Scholar]
- Ma H, Chen H, Gray L, Zhou L, Li X, et al. 2018. Changing response of the North Atlantic/European winter climate to the 11 year solar cycle. Environ Res Lett 13: 034007. https://doi.org/10.1088/1748-9326/aa9e94. [CrossRef] [Google Scholar]
- Maliniemi V, Asikainen T, Mursula K, Seppälä A. 2013. QBO-dependent relation between electron precipitation and wintertime surface temperature. J Geophys Res Atmos 118: 6302–6310. https://doi.org/10.1002/jgrd.50518. [CrossRef] [Google Scholar]
- Maliniemi V, Asikainen T, Mursula K. 2016. Effect of geomagnetic activity on the northern annular mode: QBO dependence and the Holton-Tan relationship. J Geophys Res Atmos 121: 10043–10055. https://doi.org/10.1002/2015JD024460. [Google Scholar]
- Maliniemi V, Asikainen T, Salminen A, Mursula K. 2019. Assessing North Atlantic winter climate response to geomagnetic activity and solar irradiance variability. Quart J Roy Meteorol Soc 145: 3780–3789. https://doi.org/10.1002/qj.3657. [CrossRef] [Google Scholar]
- Meehl GA, Arblaster JM, Branstator G, van Loon H. 2008. A coupled air-sea response mechanism to solar forcing in the Pacific region. J Clim 21: 2883–2897. https://doi.org/10.1175/2007JCLI1776.1. [CrossRef] [Google Scholar]
- Meehl GA, Arblaster JM, Matthes K, Sassi F, van Loon H. 2009. Amplifying the Pacific climate system response to a small 11-year solar cycle forcing. Science 325: 1114–1118. https://doi.org/10.1126/science.1172872. [CrossRef] [Google Scholar]
- Mitchell DM, Gray LJ, Fujiwara M, Hibino T, Anstey JA, et al. 2015. Signatures of naturally induced variability in the atmosphere using multiple reanalysis datasets. Quart J Roy Meteorol Soc 141: 2011–2031. https://doi.org/10.1002/qj.2492. [CrossRef] [Google Scholar]
- Ogi M, Yamazaki K, Tachibana Y. 2003. Solar cycle modulation of the seasonal linkage of the North Atlantic Oscillation (NAO). Geophys Res Lett 30: 2170. https://doi.org/10.1029/2003GL018545. [Google Scholar]
- Rayner NA, Parker DE, Horton EB, Folland CK, Alexander LV, et al. 2003. Global analyses of sea surface temperature, sea ice, and night marine air temperature since the late nineteenth century. J Geophys Res 108: 4407. https://doi.org/10.1029/2002JD002670. [Google Scholar]
- Richman MB, Lamb PJ. 1985. Climatic pattern analysis of three- and seven-day summer rainfall in the Central United States: some methodological considerations and a regionalization. J Clim Appl Meteorol 24: 1325–1343. [CrossRef] [Google Scholar]
- Roy I, Haigh JD. 2011. The influence of solar variability and the quasi-biennial oscillation on lower atmospheric temperatures and sea level pressure. Atmos Chem Phys 11: 11679–11687. https://doi.org/10.5194/acp-11-11679-2011. [CrossRef] [Google Scholar]
- Scaife AA, Ineson S, Knight JR, Gray L, Kodera K, Smith DM. 2013. A mechanism for lagged North Atlantic climate response to solar variability. Geophys Res Lett 40: 434–439. https://doi.org/10.1002/grl.50099. [CrossRef] [Google Scholar]
- Schwander M, Rohrer M, Brönnimann S, Malik A. 2017. Influence of solar variability on the occurrence of central European weather types from 1763 to 2009. Clim Past 13: 1199–1212. https://doi.org/10.5194/cp-13-1199-2017. [CrossRef] [Google Scholar]
- Sfică L, Voiculescu M, Huth R. 2015. The influence of solar activity on action centres of atmospheric circulation in North Atlantic. Ann Geophys 33: 207–215. https://doi.org/10.5194/angeo-33-207-2015. [CrossRef] [Google Scholar]
- Siddiqui TA, Yamazaki Y, Stolle C, Lühr H, Matzka J, et al. 2018. Dependence of lunar tide of the equatorial electrojet on the wintertime polar vortex, solar flux, and QBO. Geophys Res Lett 45: 3801–3810. https://doi.org/10.1029/2018GL077510. [CrossRef] [Google Scholar]
- Spiegl TC, Langematz U, Pohlmann H, Kröger J. 2023. A critical evaluation of decadal solar cycle imprints in the MiKlip historical ensemble simulations. Wea Clim Dyn 4: 789–807. https://doi.org/10.5194/wcd-4-789-2023. [CrossRef] [Google Scholar]
- van Loon H, Labitzke K. 1988. Association between the 11-year solar cycle, the QBO, and the atmosphere. Part II: Surface and 700 mb in the Northern Hemisphere in winter. J Clim 1: 905–920. [CrossRef] [Google Scholar]
- Vautard R, Mo KC, Ghil M. 1990. Statistical significance test for transition matrices of atmospheric Markov chains. J Atmos Sci 47: 1926–1931. [CrossRef] [Google Scholar]
- Wallace JM, Gutzler DS. 1981. Teleconnections in the geopotential height field during the Northern Hemisphere winter. Mon Wea Rev 109: 784–812. [CrossRef] [Google Scholar]
- Wilks DS. 2006. Statistical methods in the atmospheric sciences. 2nd ed. Academic Press, Amsterdam, Boston, Heidelberg, London, New York, Oxford, Paris, San Diego, San Francisco, Singapore, Sydney, Tokyo, p. 627. [Google Scholar]
- Woollings T, Lockwood M, Masato G, Bell C, Gray L. 2010. Enhanced signature of solar variability in Eurasian winter climate. Geophys Res Lett 37: L20805. https://doi.org/10.1029/2010GL044601. [CrossRef] [Google Scholar]
- Zhu Z, Zhou L, Zheng X. 2020. Solar wind signal in the wintertime North Atlantic oscillation and Northern Hemispheric circulation. Int J Climatol 40: 4272–4288. https://doi.org/10.1002/joc.6461. [CrossRef] [Google Scholar]
Cite this article as: Huth R & Stryhal J. 2024. Association of the 11-year solar cycle with correlation and teleconnection structures in tropospheric circulation. J. Space Weather Space Clim. 14, 31. https://doi.org/10.1051/swsc/2024031.
All Tables
Numbers of points with negative correlations (in absolute value) in the given range, separately for solar minima and maxima.
Contingency tables between phases of solar cycle (rows) and occurrence/phase of confounding forcings (columns): each entry displays the respective number of months. The last row provides χ2-statistics; asterisks denote their statistical significance at the 5% level.
All Figures
 |
Figure 1 One-point correlation maps for four points (in rows) for low (left) and high (right) solar activity. The geographical coordinates of the points are provided together with the congruence coefficient (multiplied by 100) between the two maps. Contour interval is 0.2, negative contours are dashed, zero contour is omitted. Negative values below −0.3, which are later used for the definition of teleconnected area, are shaded. Red dot indicates the base point; red cross indicates the point with most negative correlation, used for the definition of teleconnectivity. |
| In the text | |
 |
Figure 2 Congruence coefficient between one-point correlation maps for solar minimum and solar maximum multiplied by 100: black contours, contour interval 10, areas with values exceeding 80 shaded. Grid points where the correlation maps for solar maximum and solar minimum are not identical at the 10%, 5%, and 1% significance levels (i.e., are dissimilar enough) are shown in turn by red, orange, and yellow lines. NCEP-NCAR reanalysis (left) and ERA5 reanalysis (right). |
| In the text | |
 |
Figure 3 Maps for solar minimum (left) and solar maximum (middle) of teleconnectivity multiplied by 100 (top row) and normalized teleconnected area (for more details see text; bottom row). Teleconnectivity: contour interval 10, contours start at 50, values over 60 are shaded. Teleconnected area: contours 100, 200, 300, 400, 600, and 800; light and dark shading for values over 200 and 600, respectively. Differences between solar maximum and solar minimum and their statistical significance (right): differences denoted by black contours, dashed for negative values; for teleconnectivity, contour interval is 20, starting from ±10; for teleconnected area, contour interval is 200, starting from ±100; significance at the 10%, 5%, and 1% levels is denoted in turn by a thick coloured contour, light coloured shading, and dark coloured shading; positive and negative differences are shown in red and blue, respectively. |
| In the text | |
 |
Figure 4 Teleconnection diagram for solar minima (top) and solar maxima (bottom). Each point is connected by a straight line to the point with which it is most strongly negatively correlated. Only correlations (in absolute value) over 0.45 are displayed, colours denoting their strength. |
| In the text | |
 |
Figure 5 Congruence coefficient between one-point correlation maps for absence and presence of SSW, two phases of QBO, absence and presence of volcanic eruptions, and two phases of El Niño, multiplied by 100: contour interval 10, areas with values exceeding 80 shaded. |
| In the text | |
 |
Figure 6 Maps of teleconnected area for the absence/presence or two phases of SSW, QBO, volcanic eruptions, and El Niño. Contours 100, 200, 300, 400, 600, and 800; light and dark shading for values over 200 and 600, respectively. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


