| Issue |
J. Space Weather Space Clim.
Volume 2, 2012
|
|
|---|---|---|
| Article Number | A03 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/swsc/2012002 | |
| Published online | 06 June 2012 | |
Retrieval of thermospheric parameters from routine ionospheric observations: assessment of method’s performance at mid-latitudes daytime hours
1
Pushkov Institute of Terrestrial Magnetism, Ionosphere and Radio Wave Propagation (IZMIRAN), Troitsk, Moscow Region 142190, Russia
2
Institute for Space Applications and Remote Sensing, National Observatory of Athens, Metaxa and Vas. Pavlou, Palaia Penteli, 15236 Greece
3
Istituto Nazionale di Geofisica e Vulcanologia (INGV), Via di Vigna Murata 605, Rome 00143, Italy
* corresponding author: e-mail: belehaki@noa.gr
Received:
23
December
2011
Accepted:
27
April
2012
A new method has been developed to retrieve neutral temperature Tn and composition [O], [N2], [O2] from electron density profiles in the daytime mid-latitude F2-region under both quiet and disturbed conditions. A comparison with CHAMP neutral gas density observations in the vicinity of Millstone Hill Incoherent Scatter Radar (ISR) has shown that the retrieved neutral gas densities coincide with the observed ones within the announced accuracy of CHAMP observations, provided that accurate Ne(h) ISR profiles are used for the retrieval. The performance of the method has also been tested ingesting Digisonde Ne(h) profiles. In this case the agreement with CHAMP neutral gas density observations is less successful. Possible factors that can influence the performance accuracy are investigated. These are mostly related to limitations due to the ionogram scaling and inversion methods, including performance limitations of the sounding technique itself, like for instance during G-conditions. Several tests presented here demonstrate that discrepancies in the hmF2 values provided by the Digisondes could have an important impact on the performance of the method. It should be noted that in all tests performed here using Digisonde Ne(h) profiles, the topside part is approximated with the NeQuick model and any assessment concerning the impact of the topside profiler on the accuracy of the method is beyond the scope of this investigation. Despite the limitations related to the use of Digisonde profiles, the proposed method has the potential to monitor the thermosphere at least with ISR Ne(h) profiles. Digisonde electron density profiles can also be used if quality improvements are made concerning the ionogram inversion methods.
Key words: 0358: thermospheric dynamics / 7949: ionospheric storms / 2841: topside ionosphere / 2427: ionosphere/atmosphere interactions / 0394: ionosphere: instruments and techniques
© Owned by the authors, Published by EDP Sciences 2012
 This is an Open Access article distributed under the terms of creative Commons Attribution-Noncommercial License 3.0
This is an Open Access article distributed under the terms of creative Commons Attribution-Noncommercial License 3.0
1. Introduction
Hundreds of communication, military, navigation satellites orbit around the Earth and those below 2000 km are subjected to drag due to collision with the atmospheric particles. This collision slows down the spacecraft causing it to drop to lower altitudes. Following major magnetic storm activity, the atmosphere heats and expands, exerting an increased drag on satellites orbiting around the Earth. Increased atmospheric drag causes satellites to slow, lose altitude, and finally enter the dense atmosphere. Satellite operation centers have to re-identify hundreds of objects and record their new orbits after large magnetic storm events. For example, during the great geomagnetic storm of 13–14 March 1989, tracking of thousands of space objects was lost and it took North American Aerospace Defence Command many days to reacquire them in their new, lower, faster orbits. Another classic case was the premature loss of Sky Lab. Geomagnetic activity was so severe, for such an extended period, that Sky Lab de-orbited and burned in before a planned Space Shuttle rescue mission was ready to launch. Therefore, the development of methods to monitor and forecast atmospheric drag effects on satellites is a very actual problem with strong economic consequences.
Direct monitoring of the conditions in the upper atmosphere requires satellite and incoherent scatter radar (ISR) observations that are technically very complicated and expensive. The number of ISRs installed worldwide is very limited and they operate episodically. Satellite observations similar to CHAMP or TIMED/GUVI provide valuable information on the thermosphere but they can be used only for scientific research rather than applications as a single satellite cannot provide global monitoring.
Global 3D first-principle models like the Thermosphere Ionosphere Electrodynamics General Circulation Model (Richmond et al. 1992) or the Coupled Magnetosphere Ionosphere Thermosphere model (Wang et al. 2004) are powerful research tools to understand processes in the Earth’s environment. But the Earth’s upper atmosphere is an open system that receives considerable energy and momentum from the lower atmosphere as well as from the Sun and the magnetosphere. If the impact from the above can be controlled to some extent, the impact from below (tides, gravity waves, tropospheric electric fields) cannot be controlled in principle. Moreover, the response of the upper atmosphere to one and the same impact will be different depending on the prehistory of the state of the magnetosphere and ionosphere. So it is not surprising that such very sophisticated first-principle models demonstrate shortcomings (e.g., Lei et al. 2008, 2011). Problems with model description of disturbed conditions were stressed repeatedly. Prölss et al. (1998) have analyzed DE-2 neutral composition observations along with CITM and TIGCM model predictions for the 8 December 1982 geomagnetic storm. It was shown that both models strongly overestimate the O/N2 enhancement predicting the O/N2 increase as large as 130% in the evening sector, whereas the measured changes were less than 30%. Kil et al. (2011) have compared the TIMEGCM simulations with GUVI observations during the 20 November 2003 storm. In the American sector, the O/N2 ratio, at the F peak height, increases by a factor of 3–5 in the model results, while GUVI corresponding observations demonstrate only a minor change. Therefore, it is not clear if such models can be efficiently used for the upper atmosphere monitoring in real time.
Semi-empirical atmospheric density models, such as DTM-94 (Berger et al. 1998), DTM-2000 (Bruinsma et al. 2003), and MSIS-86 (Hedin 1987), were evaluated by Bruinsma et al. (2004), comparing the modeled density with CHAMP/STAR densities. The global mean of the density ratios showed that the models underestimate density by 10–20% with an rms of 16–20% for quiet (ap < 15) geomagnetic condition.
Although Bruinsma et al. (2004) have pointed out that the accuracy of CHAMP neutral density observations was not known for disturbed conditions due to unmodeled neutral atmosphere winds, one may find in Lathuillère et al. (2008) an analysis of CHAMP/STAR observations for disturbed conditions and a comparison with the MSISE-00 model (Picone et al. 2002). This comparison has shown that “the model statistically underestimates the density disturbance by about 50% for magnetically activity levels less than Kp ~ 6. During more disturbed conditions the model can underestimate the density disturbance amplitude by more than 200%”. The analysis of CHAMP and GRACE neutral density variations during the 20–21 November 2003 geomagnetic storm has shown that the MSISE-00 model underestimates strongly by two times the neutral density disturbance effect (Bruinsma et al. 2006).
An alternative approach is being proposed in this paper and it is based on the idea that the ionosphere is a child of the Sun and the upper atmosphere. Consequently, the ionospheric Ne(h) profile contains the whole information on the ionizing solar extreme ultraviolet radiation (EUV) radiation, neutral composition, temperature height distribution, and thermospheric winds and therefore, it is possible in principle to retrieve the main aeronomic parameters responsible for the formation of the Ne(h) profile, solving an inverse problem. Following this concept, the work presented in this paper exploits recent advances in ionospheric monitoring and modeling for the development of a method able to monitor the upper atmosphere. Although the Earth’s upper atmosphere is mainly composed by neutral atoms and molecules as the share of ionized particles is small (even at the ionospheric F2-layer maximum, around an altitude of 300 km, the concentration of [O+] ≈ Ne comprises only 0.1% of the total particle concentration), the exploration of the Earth’s ionosphere has been started much earlier (in 1920s) than the upper atmosphere (in 1960s) and currently our knowledge of the ionosphere is wider and more systematized. This is due to the simplicity of the ionospheric observations. Ground-based ionosondes operate all over the world and have performed already for several solar cycles, providing a vast database on electron concentration variations in E, F1, and F2 ionospheric layers under various geophysical conditions. Modern digital ionosondes have the possibility to calculate the electron density Ne(h) profiles in real time. Data repositories of real time ionospheric observations (Reinisch et al. 2004; Belehaki et al. 2006) allow access through the Internet, opening new opportunities for monitoring and modeling the ionosphere but also the upper atmosphere. However, two conditions should be fulfilled for the success of the proposed method: (a) the electron density profile Ne(h) should be accurate enough, especially in the vicinity of the F2 maximum, and (b) the rates of processes forming this profile are supposed to be known with a sufficient accuracy also.
A self-consistent approach to the F-region modeling using ISR observations has been proposed by Mikhailov & Schlegel (1997) with further modifications by Mikhailov & Lilensten (2004). This method uses ISR observations: Ne(h), Ti(h), Te(h), V(h) profiles. Solving an inverse problem of aeronomy it is possible to find neutral composition [O], [O2], [N2], height profile of Tn(h), vertical plasma drift W(h), which can be converted to the effective meridional thermospheric wind, and total EUV flux with λ ≤ 1050 Å responsible for the F2-region ionization. This approach provides all important aeronomic parameters simultaneously in a self-consistent way. It has been used to analyze the formation mechanisms of the F2-layer both under quiet and disturbed conditions using Millstone Hill and EISCAT ISR observations (e.g., Mikhailov & Förster 1997, 1999; Mikhailov & Schlegel 2003; Mikhailov & Perrone 2011).
In this paper we propose a new method, which is analog to the Mikhailov & Lilensten (2004) model, but modified to use as input only ionospheric Ne(h) profiles. However, there are several issues that should be considered. Unlike ISR observations for which important parameters such as plasma temperatures Te, Ti, and vertical plasma velocity Vi are known simultaneously with the electron density, in the case of ionosonde observations we have only bottomside Ne(h) profile. Moreover, the height accuracy of such profiles may be different than that of ISR observations, and this will be investigated in Section 4. Therefore in this paper, we concentrate on the following tasks:
-
to develop a method extracting basic thermospheric parameters from Ne(h) profiles,
-
to test the method using both Digisonde and ISR Ne(h) profiles in a comparison with CHAMP/STAR neutral gas density observations under various geophysical conditions,
-
to investigate the limitations of this method, especially concerning its implementation in real time.
2. Description of the method
For the convenience of reading we are presenting a brief description of the method mentioning the differences from the basic version (Mikhailov & Schlegel 1997; Mikhailov & Lilensten 2004). The analysis presented here is focused on the model performance under sunlit conditions at middle latitudes. The roles of different atmospheric species are more distinct under the influence of the ionizing solar EUV and this should help separate them solving the inverse problem of aeronomy. The initial basic method has been developed using reliable ISR Ne(h) profiles. In the method we propose here, Digisonde Ne(h) profiles will be used optionally as the input. Millstone Hill ISR and Digisonde simultaneous observations provide an appropriate data set for such analysis.
2.1. Ionospheric model
The ionospheric model is the instrument used in our method to split the observed Ne(h) profile into the aeronomic parameters creating this Ne(h) distribution. It should be simple as much as possible to be an operative one and to take into account the main processes responsible for the formation of the daytime mid-latitude F2-layer. The list of processes is well known: (a) photo-ionization of neutral [O], [O2], [N2] species by solar EUV, (b) transfer of O+ ions by diffusion, thermospheric winds and electric fields, and (c) plasma recombination in the chain of ion-molecular reactions. Therefore, our model includes transport process for O+(4S) and photo-chemical processes only for O+(2D), O+(2P), O2 +(X2∏), N+, N2 +, and NO+ ions in the 170–550 km height range. A two-component model of the solar EUV from Nusinov (1992) is used to calculate photo-ionization rates in 48-wavelength intervals (10–1050) Å. The photo-ionization and photo-absorption cross-sections are obtained from Torr et al. (1979), Richards & Torr (1988), Richards et al. (1994), and Ivanov-Kholodny & Nikoljsky (1969) for X-ray emission. The list of chemical processes used in the model is given in Mikhailov & Lilensten (2004). More recent chemical reaction rate constants may be found, for instance, in Richards (2011).
Concentration of O+(4S) ions is calculated from the continuity equation (1)where
(1)where (2)
Vi is total vertical velocity of plasma and W is vertical plasma drift due to thermospheric winds and electric fields. Neglecting electric field effects which are not known in routine ionospheric observations W may be converted into the effective meridional thermospheric wind using the expression
(2)
Vi is total vertical velocity of plasma and W is vertical plasma drift due to thermospheric winds and electric fields. Neglecting electric field effects which are not known in routine ionospheric observations W may be converted into the effective meridional thermospheric wind using the expression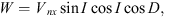 (3)where I and D are magnetic inclination and declination.
(3)where I and D are magnetic inclination and declination.
The shape profile for vertical plasma drift is not known a priori for particular geophysical conditions. Our testing of various shapes for vertical plasma drift has shown that W(h) profiles given in Figure 1 can be used for our aims. Horizontal thermospheric winds varying with altitude were shown to take place in the upper atmosphere both under quiet and disturbed conditions (Wang et al. 2008). During the fitting procedure the corresponding (Quiet or Disturbed) W(h) profile is shifted as a whole. The type of ionospheric conditions (Quiet or Disturbed) is always known comparing currently observed foF2 with the running foF2 median. At this stage we do not distinguish positive from negative F2-layer disturbances and use the same W(h) profile for disturbed conditions.
 |
Fig. 1. Height dependences for vertical plasma drift in magnetically quiet and disturbed conditions. |
Diffusion collision frequencies vij for O+ are related to momentum transfer collision frequencies v* by the expression (see Eq. (19.13) in Banks & Kockarts 1973) vij = mj/(mi + mj) v*ij, where i applies to O+ ions and j applies to other neutral or ionized gas species. Collisions of O+ ions with neutral O, O2, N2 and only with NO+, O2+ ions are taken into account. All O+ ion collision frequencies are taken from Banks & Kockarts (1973). A correction factor 1.2 for vO+−O was applied in accordance with the results of analyses by Pesnell et al. (1993), Oliver & Glotfelty (1996), Buonsanto et al. (1997), Litvin et al. (2000). The vij, qi, β values in equations (1) and (2) depend on the aeronomic parameters which are searched for.
Normally the results of calculations are rather insensitive to the choice of the upper boundary height within the 400–600 km range (Mikhailov & Kofman 2001). Therefore, we take the upper boundary at 400 km under solar minimum, at 500 km under solar medium, and at 550 km under solar maximum conditions supposing that [O+] = Ne is observed at this height. Normally the low boundary for [O+] is specified at 160–180 km where [O+] is supposed to be in the photo-chemical equilibrium.
There are both stationary and non-stationary versions of the method. In the case of a non-stationary solution the height profile of O+ ions from the previous time step should be specified. In the case of searching for a stationary solution the same scheme is used with iterations until a stable solution is obtained. A comparison has shown that two solutions give close results and normally a stationary solution can be used during daytime hours. However even during daytime, non-stationary conditions may take place and such cases were omitted from our analysis at this stage.
2.2. The energy balance equation
Electron and ion temperatures are not the parameters which are of our main interest but they are used in the continuity equation (1) and should be specified. An accurate calculation of plasma temperatures is a very complicated task (Banks & Kockarts 1973). For our method we need a simple and fast working method which could be efficiently used in the iterative procedure of the thermospheric parameter retrieval. Solving the energy balance equation we will consider the same height range as for the continuity equation (1) with the upper boundary condition for Te which is a fitting parameter in the method. Inside the area we consider only local heating of the electron gas (Banks & Kockarts 1973; Munninghoff 1979):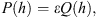 (4)where ε is the heating efficiency and Q is the total photo-ionization rate, ε being a fitting parameter as well.
(4)where ε is the heating efficiency and Q is the total photo-ionization rate, ε being a fitting parameter as well.
The expressions for electron cooling processes can be found in (Banks & Kockarts 1973; Munninghoff 1979).
Electron thermal conductivity is included inside the area. The expression for Ke may also be found in (Banks & Kockarts 1973).
The balance equation for the electron gas may be written as follows:![$$ \frac{3}{2}k{N}_{\mathrm{e}}\frac{\mathrm{\partial }{T}_{\mathrm{e}}}{\mathrm{\partial }t}=\frac{\mathrm{\partial }}{\mathrm{\partial }h}\left[{K}_{\mathrm{e}}\frac{\mathrm{\partial }{T}_{\mathrm{e}}}{\mathrm{\partial }h}\right]-{L}_{\mathrm{e}}+q, $$](/articles/swsc/full_html/2012/01/swsc110035/swsc110035-eq5.gif) (5)where Ne is the electron concentration, Te is the electron temperature, k is Boltzmann’s constant, Ke is the thermal conductivity for the electron gas, Le is the total cooling rate, and q is the total heating rate of the electron gas which includes both local heating related to photo-ionization and heating coming from processes of the electron gas with neutrals and ions. Depending on the (Te−Ti) and (Te−Tn) sign some processes may work as heating or cooling the electron gas and they are prescribed either to q or to Le terms in equation (5).
(5)where Ne is the electron concentration, Te is the electron temperature, k is Boltzmann’s constant, Ke is the thermal conductivity for the electron gas, Le is the total cooling rate, and q is the total heating rate of the electron gas which includes both local heating related to photo-ionization and heating coming from processes of the electron gas with neutrals and ions. Depending on the (Te−Ti) and (Te−Tn) sign some processes may work as heating or cooling the electron gas and they are prescribed either to q or to Le terms in equation (5).
Equating the ion thermal energy input from electron-ion collision to that lost through collisions with neutral particles, an approximate expression for the ion temperature can be obtained ignoring thermal conduction (Banks & Kockarts 1973):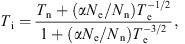 (6)where α ≈ 6 × 106 and Nn is the neutral gas number density.
(6)where α ≈ 6 × 106 and Nn is the neutral gas number density.
2.3. Measured input parameters
The list of measured input parameters includes indices of solar and geomagnetic activity: F10.7 for current and previous days as well as the 81-day running mean F10.7 value, a background F10.7 value used in the solar EUV model by Nusinov (1992), and daily Ap index used in the MSIS-86 model. The background F10.7 is a smooth varying function whose values change from ~65 under solar minimum up to ~120 under solar maximum (Nusinov 1984). The main measured input parameter is the Ne(h) profile. In this method we use two sources of getting the Ne(h) profile, the ISR and the Digisondes. While ISR provides the whole electron density profile (usually up to ~700 km), Digisondes perform measurements only for the bottom part of the ionosphere up to the height of the maximum concentration (hmF2). ARTIST software (Reinisch & Huang 1983; Reinisch et al. 2005; Galkin et al. 2008) makes the ionogram inversion and delivers the Ne(h) profile up to hmF2. For the purposes of this work we need not only the bottomside profile but also the extrapolated part up to the 400–500 km. Reinisch & Huang (2001) have developed and implemented in the Digisonde built-in software, a simple approximation for the topside extrapolation. The profile above the peak is approximated by an α-Chapman function with a constant scale height derived from the bottomside profile shape at the F2 peak. As it was demonstrated earlier (e.g., Belehaki et al. 2003), this approximation as a rule is not valid for the topside ionosphere, therefore a more precise extrapolation method is needed. The NeQuick model (e.g., Di Giovanni & Radicella 1990; Radicella & Leitinger 2001; Nava et al. 2008) improves the extrapolation accuracy, at least for the middle latitudes, where this paper is concerned. Other efforts are under development: the TaD model (Belehaki et al. 2009; Kutiev et al. 2009) based on the reconstruction of topside density profile by using the topside sounder model profiler and Digisonde data; the new Vary-Chap model of topside electron density profiles based on ISIS-2 sounding data (Reinisch et al. 2007, 2011; Bilitza et al. 2011). Both methods show a good performance, but since they are still under validation, for the purposes of this investigation we will adopt the NeQuick model to extrapolate the bottomside ARTIST profiles. Observed NmF2 and hmF2 values from the ARTIST profile are used in the NeQuick model.
2.4. Retrieved parameters
An important point is the list of aeronomic parameters to be searched for. These should be the main parameters responsible for the F2-region formation. An analytical solution of the continuity equation for electron concentration in the F2-region (e.g., Ivanov-Kholodny & Mikhailov 1986) can help select the parameters. In the mid-latitude daytime F2-region they are: neutral temperature Tn, atomic oxygen [O], linear loss coefficient β = γ1[N2] + γ2[O2], efficiency of solar ionization, and vertical plasma drift W due to thermospheric winds and electric fields.
All aeronomic parameters may be divided into two groups: rate constants of the processes, relative energy distribution over the solar EUV spectrum which are supposed to be known and those which vary with geophysical conditions. The latter are our main concern.
In the basic method which uses ISR Ne(h), Te(h), Ti(h), and VO(h) profiles seven parameters are retrieved: three parameters (Tex, S, T120) specifying Tn(h) profile, factors for the MSIS-86 model [O], [O2], [N2] concentrations as well as for the total solar EUV flux with λ < 1050 Å. Vertical plasma drift W(h) is calculated at each step of fitting using equation (2).
However in the method being developed, we have only Ne(h) profile as the measured input ionospheric source of information and this is not enough to find all the parameters mentioned. The list of retrieved parameters necessary to solve our problem includes: exospheric temperature Tex along with the shape parameter S, factors for the MSIS-86 model [O], [O2], [N2] concentrations, vertical plasma drift W plus two parameters to calculate plasma temperatures (electron temperature at the upper boundary Teupp and ε is the heating efficiency). The total EUV flux and T120 are not fitted but taken from the models in accordance with geophysical conditions. The EUV solar flux is taken from the Nusinov (1992) model and T120 from MSIS-86 model (Hedin 1987). The input parameters of this type may be called as model input parameters. They also vary with geophysical conditions and are used as they are in the empirical models.
The extraction of thermosphere parameters from ionospheric ones is a problem of nonlinear programming (Himmelblau 1972).
2.5. Fitting procedure
To fit the observed Ne(h) profile eight aeronomic parameters (Tex, S, FacO, FacO2, FacN2, W, Teupp, and ε) should be found. However among these parameters, Tex is a special one. Exospheric temperature is the key parameter which cannot be found along with the other parameters within one algorithm and a special method has been developed for its determination. The process starts with searching for Tex. The method is run for different Tex in a wide range of Tex values with a small (1–5) deg step. The Tex interval should be 100–150 K around the MSIS-86 Tex value. The remaining seven parameters are fitted simultaneously at each iteration step. The quality of Ne(h) fitting depends on Tex and normally there exists the global minimum in delta specified as: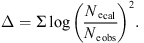 (7)
(7)
Exospheric temperature Tex corresponding to this global minimum is used for the final model run. Sometimes the Δ(Tex) dependence has some local minima and the global minimum is found at a very low and unreal Tex. On the other hand, the quality of Ne(h) fitting may be sufficient in one of the local minima keeping in mind the limited accuracy of the experimental Ne(h) profiles. To overcome this ambiguity an additional parameter R has been introduced: (8)where ρ is the neutral gas density which always increases with Tex at given height. The global maximum of R corresponds to one of the local minima in the Δ(Tex) dependence under the maximal possible ρ value. Normally two Tex values obtained with the two methods do not coincide and the average of two Tex is taken in this case. Sometimes only one parameter gives Tex reliably and it is used as the final value for calculations. Two cases for Tex specification are given in Figure 2 as an example. Top panels show a case when the two extremes are specified reliably and Tex values obtained from the two parameters are close to each other. Lower panels demonstrate a case when Tex can be found reliably only from one parameter, R as the Δ parameter gives a plateau in a wide range of Tex values.
(8)where ρ is the neutral gas density which always increases with Tex at given height. The global maximum of R corresponds to one of the local minima in the Δ(Tex) dependence under the maximal possible ρ value. Normally two Tex values obtained with the two methods do not coincide and the average of two Tex is taken in this case. Sometimes only one parameter gives Tex reliably and it is used as the final value for calculations. Two cases for Tex specification are given in Figure 2 as an example. Top panels show a case when the two extremes are specified reliably and Tex values obtained from the two parameters are close to each other. Lower panels demonstrate a case when Tex can be found reliably only from one parameter, R as the Δ parameter gives a plateau in a wide range of Tex values.
 |
Fig. 2. Determination of Tex. Triangles – Δ and ρ/Δ values obtained in calculations with various Tex. Solid line – the 5th order polynomial approximation. Arrows indicate the extreme positions. Top panels illustrate a “good” case when Tex is found reliably from Δ and ρ/Δ parameters. In the second case (lower panels) the Δ parameter exhibits a plateau in a wide range of temperatures and Tex can be found only from one parameter, ρ/Δ. |
The quality of the Ne(h) fitting is shown in Figure 3 with two examples, one of the best and one of the worst fitting. Millstone Hill ISR observed Ne(h) profiles were used in these calculations.
 |
Fig. 3. Two examples illustrating the quality of the observed Ne(h) profiles fitting with the method. Solid lines – Millstone Hill ISR observed profiles, dashes – the results of calculations. One good and one bad cases of fitting are shown. |
For the convenience of reading Table 1 summarizes the input parameters of the both measured and model ones used in the method as well as the retrieved parameters followed by the explaining comments.
List of input (both measured and model) parameters used in the method and the retrieved ones.
3. Testing of the method
The purpose of this section is to test the method’s performance and to identify possible limitations in its accuracy (e.g., dependence of the method’s performance on the accuracy of the Ne(h) profiles and hmF2).
The first test is the self-retrieval, i.e. to check if the method can retrieve the input aeronomic parameters from the calculated Ne(h) profile. Table 2 gives an example of such self-retrieval for 14 October 2002. In general, all the results verify that there are some differences between the input and the calculated values, but these are small and in any case they are within the standard error of our calculations, which may be estimated as ±10% for Tex and about ±20% for neutral species (Mikhailov & Lilensten 2004). One of the possible reasons for these discrepancies of the self-retrieval is that all calculations are made with a single precision.
Thermospheric parameters used to calculate Ne(h) in the direct model run and the retrieved from this Ne(h) profile neutral composition, temperature, and wind.
The second test is crucial and concerns the comparison for the model results with CHAMP/STAR accelerometer observations of the neutral gas density. These excellent observations have been conducted for many years under various geophysical conditions and they open a wide opportunity to test the method. Millstone Hill is selected as the test site, since ISR and Digisonde experiments collocate and therefore it will be possible to test the method’s performance by all aspects.
Millstone Hill ISR conducted a long duration 30-day experiment in October 2002. The results of observations can be found at http://madrigal.haystack.mit.edu/madrigal/. ISR observations need a special reduction before being used in calculations. Each particular height profile Ne(h) is not smooth exhibiting fluctuations for some reasons and cannot be used for solving the inverse problem. Therefore, median (not average) profiles are calculated over (1.0–1.5) hour time interval which is close to the e-fold time of the daytime F2-layer. These median vertical profiles are then smoothed by a polynomial of up to 5th degree before being used in our model calculations.
CHAMP neutral gas density observations (http://sisko.colorado.edu/sutton/data.html) are available in the American longitudinal sector for October 2002 during daytime hours and this was a fortunate coincidence. The height of CHAMP orbit was near 400 km that time, therefore neutral gas density was reduced to Millstone Hill location and 400 km height using MSISE-00 (Picone et al. 2002) thermospheric model and the following expression:
The height for the reduction should be close to the satellite height to minimize possible errors due to the MSISE-00 imperfectness. Three successive observations close in latitude and longitude to Millstone Hill (42.6 N, 288.5 E) were averaged to give the neutral gas density for our comparison. Normally the reduced values of ρ from three points are close, so the averaged value is reliable.
The October 2002 period was very interesting for this testing as it comprised both quiet and strongly disturbed days. It should be noted that this interval corresponds to solar maximum conditions. Figure 4 gives the variations of daily F10.7, daily Ap, and 3-hour ap for the selected UT moments. Millstone Hill ISR and Digisonde hmF2 and NmF2 are also shown for comparison and evaluation.
 |
Fig. 4. The observed daily F10.7, the daily Ap (solid), and 3-hourly ap(dots) indices for the period 4–30 October 2002. Millstone Hill ISR and Digisonde-hmF2 and -NmF2 values, corresponding to local noon observations, are also shown for a comparison. |
The first half of the period (October 4–16) was more disturbed than the second half and strong day-to-day NmF2 variations took place. The second part was more stable with moderate positive NmF2 disturbances compared to the monthly median (not shown here) observed. It is worthy to note that the Digisonde-hmF2 measurements are systematically lower than the corresponding values obtained from ISR and this was reported earlier by Chen et al. (1994). Digisonde-NmF2 values are slightly but systematically larger than ISR-NmF2 values during the second part of this interval.
The model extracted neutral gas density ρ = m1[O] + m2[N2] + m3[O2] at 400 km height is given in Figure 5 in a comparison with CHAMP neutral gas density observations, reduced to the location of Millstone Hill. The MSISE-00 (Picone et al. 2002) and JB2006 (Bowman et al. 2008) model predictions are also given in this plot. Here, ISR-Ne(h) profiles were used in these model calculations. The absolute uncertainty of CHAMP neutral gas density observations is 10–15% (Bruinsma et al. 2004), therefore ±10% error bars are added to CHAMP data in Figure 5. The results of calculations for all 16 days are seen to be in the ±10% interval. Naturally, empirical (statistical) models are unable to reproduce well day-to-day neutral gas density variations. However, JB2006 is seen to describe better relative variations comparing to the MSISE-00 model. An additional comparison of CHAMP neutral gas density observations with MSISE-00 and JB2006 empirical models is presented in Section 4.
 |
Fig. 5. Reduced to the Millstone Hill location and 400 km height CHAMP neutral gas density observations along with ±10% error bars, MSISE-00 and JB2006 model predictions and the model extracted neutral gas density at 400 km height using ISR Ne(h) profiles. |
A similar comparison has been done for solar minimum conditions using Millstone Hill ISR and CHAMP neutral gas density observations for several days in January 2008. Regardless of the extremely quite geomagnetic activity conditions during this period, unstable (non-stationary) conditions took place in the F2-region parameter variations for some days. These days were omitted from our analysis as at this stage a stationary method of calculations is used. The altitude of CHAMP satellite was close to 340 km in January 2008 therefore the observed neutral gas density was reduced to 340 km. Figure 6 gives daily F10.7, daily Ap, and 3-hour ap for the selected UT as well as Millstone Hill ISR and Digisonde-hmF2 and -NmF2 variations. That was a deep solar minimum with F10.7 = 71–72. Daytime F2-layer was at 220–230 km with a very low maximum electron density NmF2 ranging from 3 to 4 × 105 cm−3. Similar to the October 2002 case Digisonde-hmF2 measurements are systematically lower than the ISR-hmF2 values.
The model calculated neutral gas density at 340 km in a comparison with the reduced CHAMP observations and MSISE-00 and JB2006 model predictions are given in Figure 7. Except for one point all the calculated neutral gas densities are in the ±10% corridor around CHAMP observations. Although the model calculated values are close to the observed ones, they slightly but systematically overestimate the observations and this may be indicative of some inconsistencies of the proposed method for solar minimum conditions. The MSISE-00 model overestimates the observed values and this was noted earlier (e.g., Bruinsma & Forbes 2010), while JB2006 reproduces the observed neutral density variations much better.
The obtained results tell us that the proposed method seems to be efficient if reliable ISR Ne(h) profiles are used. Of course, this is an important result as a vast database with Millstone Hill ISR observations under various geophysical conditions exists and a possibility to extract basic thermospheric parameters from these observations is of great interest. However, ISRs perform only in limited locations over the globe. For potential operational implementation of this method globally, it is necessary to investigate the possibility to exploit Ne(h) profiles from Digisondes, which form a dense network.
The third test is presented here that concerns assessment of model’s performance using as input Digisonde Ne(h) profiles. The calculations were repeated for October 2002 and January 2008 periods using Digisonde bottomside profiles in combination with NeQuick topside extrapolations over Millstone Hill. Then median values calculated over 1 hour of observations and smoothed Ne(h) profiles were constructed. This has been done for two reasons. On one hand ISR profiles used in our calculations were prepared in this way. One the other hand at this stage we work with the stationary method and the observed Ne(h) profiles should be averaged over 1–1.5 hour time interval (e-fold time) to be used in the method. Figure 8 gives the model results of the neutral gas density calculations for October 2002, under solar maximum conditions. For 13 dates the calculated neutral gas densities are in the ±10% corridor however a tendency for the calculated ρ to be lower than the observations is seen. On October 12, 14, and 15 the calculations are much below the observed values. The cause of this discrepancy will be analyzed further in Section 4.
 |
Fig. 8. CHAMP neutral gas density observations, reduced to the location of Millstone Hill, along with ±10% error bars and the model calculated neutral gas density at 400 km height using Digisonde/NeQuick model profiles, for October 2002 (solar maximum). |
The calculations were also performed for January 2008 (Fig. 9), for solar minimum conditions. In general the results are similar to October 2002. The model neutral gas density is systematically lower than the observed values and this difference is larger for solar minimum conditions compared to solar maximum (Fig. 8).
 |
Fig. 9. Same as Figure 8 for January 2008, for solar minimum conditions. The comparison is made at 340 km. |
4. Discussion
The undertaken analysis attempts to investigate the level at which the inverse problem of aeronomy, i.e. the retrieval of thermospheric parameters from observed Ne(h) profiles, can be successfully resolved with the proposed method, ingesting Ne(h) profiles from ISR and Digisondes.
Currently, the only possibility to monitor the thermosphere is to use empirical (statistical) thermospheric models. These models rely very heavily on the assimilated density data. Predictions under conditions for which no or (too) few data were available, or inaccurate data were assimilated, may be significantly in error (Bruinsma et al. 2004).
A comparison of CHAMP observations with the MSISE-00 (Picone et al. 2002) thermospheric model (Figs. 5 and 7) shows that MSISE-00 on one hand systematically overestimates the neutral gas density, on the other hand it does not reproduce relative day-to-day variations in ρ (e.g., Fig. 5) clearly seen in CHAMP observations. The results for JB2006 model look much better. To confirm this result, this comparison has been extended for the whole October 2002 and February 2008 using statistically sufficient number of cases. The results are given in Figure 10 and in Table 3.
 |
Fig. 10. Histograms for CHAMP/model ratios for October 2002 (solar maximum) and February 2008 (solar minimum). MSISE-00 and JB2006 models were used for a comparison. The comparisons were made at 400 km for October 2002 and at 340 km for February 2008. |
Comparison of MSISE-00 and JB2006 model predictions with CHAMP neutral gas density observations for the periods of solar maximum (October 2002) and solar minimum (February 2008) activity. Standard deviation and mean relative deviation are given, analyzing a total number of 2414 measurements.
These results demonstrate that both models underestimate CHAMP observations in October 2002: MSISE-00 by 17% and JB2006 by 11%. In February 2008 MSISE-00 strongly (>40%) while JB2006 slightly (~15%) overestimate the CHAMP observations. These model deviations from the observations cannot be related with the data reduction to fixed heights as the height of CHAMP orbit was close to 400 km in October 2002 and it was around 340 km in February 2008. In general JB2006 is seen to demonstrate better results both in SD and MRD characteristics. This was earlier also shown by Bowman et al. (2008, see their Fig. 17).
The histograms in Figure 10 show that large deviations of model values from observations can occur. This is a well-known problem of all empirical (statistical) models, due to the very method of their construction they cannot properly describe individual large day-to-day variations. On the other hand, the ionosphere follows day-to-day variations in the thermosphere (the reasons for these variations may be a lot) and it can give information on the thermosphere current state. Therefore, the proposed method based on the analysis of Ne(h) profiles in principle shows the way for more efficient thermospheric monitoring.
Given the real necessity to develop a reliable method that can be applied to any geographic location under any geophysical conditions, a further assessment of the results obtained here is attempted. This method was first tested with ISR data and compared with CHAMP density measurements. The accuracy was within the limits of the STAR measurements (±15%) and the performance was comparable to the JB2006 model. Routine Digisonde Ne(h) profiles were also considered as input to the proposed method. In this case, considerable limitations in the method’s performance were detected. As Digisonde observations provide only the bottomside Ne(h) profile, limitations can be either due to inaccuracies in the ionogram inversion method and/or due to the reliability of the reconstructed topside profile. For the purposes of this work, NeQuick extrapolated profiles are used, but again the method’s performance is poorer than in the case of using ISR profiles. This is more evident during solar minimum conditions. To discuss further this point, we focus on the difference between ISR and Digisonde hmF2 estimations noted in Section 3. In particular, Digisonde hmF2 estimations were systematically lower than the ISR ones in all presented examples in Figures 4 and 6. Low hmF2 implies low thermospheric temperature that results in low neutral gas density at a fixed height and therefore it may explain the underestimation of the neutral gas density provided by the proposed method in respect to the CHAMP observations (Figs. 8 and 9).
To further approach this problem, we can go back to the test period of October 2002. Figure 8 shows that the calculations gave very low neutral gas density for three dates: October 12, 14, and 15, 2002. Table 4 gives hmF2 from Digisonde and ISR Ne(h) profiles as well as calculated Tex using these profiles. In all three cases Digisonde hmF2 are much lower than ISR ones. Low hmF2 yield in low thermospheric temperature and Table 4 does show these low Tex compared to Tex retrieved from ISR Ne(h). Low neutral temperature results in low neutral gas density at a fixed height (400 km in our case). Therefore, low Digisonde hmF2 observed for these dates may be considered as the reason for low neutral gas density obtained in our calculations while ISR Ne(h) give acceptable ρ values for the same dates (Fig. 7).
Calculated neutral gas density using Digisonde Ne(h) profiles extrapolated with NeQuick for three dates with SAO hmF2 much lower ISR hmF2 values.
From the practical point of view it may be useful to know the effect of small hmF2 variations in the method’s results. Here we only give the results of an Ne(h) shift as a whole, but in reality the shape of Ne(h) profile should also change along with hmF2 changing and this should result in additional variations of the retrieved thermospheric parameters. Table 5 gives the calculated thermospheric parameter when the whole Ne(h) profile is shifted by +5 to −20 km. The same 14 October 2002 day was considered.
Thermospheric parameters variation resulted from Ne(h) shift as a whole by +5 to −20 km. The accuracy Δ of Ne(h) fitting is also given.
Table 5 shows that a downward Ne(h) shift by 25 km corresponds to the Tex decrease by ~ 6% and the neutral gas density decrease at 300 km by ~20%, which consists of ~9.5% decrease in [O], ~30% decrease in [N2], and ~27% decrease in [O2]. The accuracy Δ of fitting is seen to decrease when the Ne(h) profile is shifted downward. Lower hmF2 may result in a low fitting accuracy and low calculated neutral gas density.
Although a ±10 km shift in hmF2 is not important for HF communication purposes, it has a measurable effect on the results of this specific application.
Inaccurate hmF2, if exists, is a source of a systematic error for this method. Moreover, the method cannot work under specific geophysical conditions, if Digisonde Ne(h) profiles are used. An example of such conditions is presented in Figure 11. During strong negative disturbances like the one observed on 15 December 2006 at Millstone Hill, Digisonde observed F1-layer maximum (G-conditions) and any information on the F2-layer was absent in principle.
 |
Fig. 11. Observed at Millstone Hill F2-layer maximum parameters along with AE index variations for 13–15 December, 2006. Triangles – Digisonde, circles – ISR observations, dashes – 27-day running medians calculated from Digisonde data. LT = UT-5. |
Under quiet (13 December 2006) and positive storm phase (14 December 2006) daytime Digisonde hmF2 values are close to ISR height measurement with a tendency to lower values. This difference was discussed earlier by Chen et al. (1994). Under negative storm phase on 15 December 2006 Digisonde hmF2 values are systematically lower than ISR hmF2 as under G-conditions the Digisonde observes F1-layer as the main ionospheric maximum. This shows that a qualitative analysis of ionospheric conditions should be performed before ingesting the Ne(h) Digisonde profiles to our model, in order to eliminate use of ionograms that could result to misleading calculations for the neutral density.
Finally, it should be stressed that the proposed method is not only designed to calculate the neutral gas density. Empirical models like Bowman et al. (2008) or Emmert & Picone (2010) are also able to describe this thermospheric parameter with an acceptable accuracy on average. The proposed method allows us to retrieve a self-consistent set of the basic thermospheric parameters: neutral temperature, atomic oxygen, molecular nitrogen, and to some extent molecular oxygen which varies in the frame of MSIS-86 model along with neutral temperature in the iterative process of Ne(h) fitting. At present there is no possibility to compare the calculated neutral composition with any direct observations – neutral gas density provided by CHAMP is the integral characteristic of the thermosphere which includes the contributions both from neutral composition and temperature. However, indirect checks can be done. For instance, analyzing the Ne(h) profiles which correspond to negative (14 October 2002) and a small positive (28 October 2002) F2-layer storms, the method gives different O/N2 ratios at 300 km: 1.6 for October 14 and 7.0 for October 28 in accordance with the present-day understanding of the F2-layer storm mechanisms. MSISE-00 predicts very moderate O/N2 ratio variations: 3.8 for October 14 and 4.6 for October 28. The enrichment of the thermosphere with heavy molecular species during negative storms should result in ion composition enriched with molecule ions and this does take place. Figure 12 gives O+/Ne ratio for these two days in a comparison with the standard ion composition model used at Millstone Hill during the autocorrelation function analysis.
 |
Fig. 12. Calculated relative ion composition for the periods of negative and positive F2-layer storms. The standard Millstone Hill ion composition model is given for a comparison. |
The ionosphere strongly enriched with heavy molecule ions NO+ and O+ below 250 km during negative storm day is seen in Figure 12. Positive storm effect is mostly related to thermospheric winds rather than neutral composition changes (Prölss 2004). For this reason the relative ion composition is close to the standard model. This comparison also demonstrates the efficiency of the proposed method.
5. Conclusions
-
For the first time it was shown a principal possibility to retrieve a self-consistent set of the main thermospheric parameters (Tn, [O], [N2], [O2]) from electron density profiles in the daytime mid-latitude F2-region.
-
A comparison with CHAMP neutral gas density observations both under solar maximum (October 2002) and solar minimum (February 2008) conditions has shown that the retrieved gas densities are in the ±(10–15)% corridor corresponding to the absolute inaccuracy of CHAMP observations, provided that accurate Ne(h) ISR profiles are used for the retrieval. This is an important result as there exists a vast database with Millstone Hill ISR observations under various geophysical conditions and a possibility to extract basic thermospheric parameters from these observations is of great interest.
-
The implementation of the method with Digisonde Ne(h) profiles shows a less successful performance, compared to the results obtained using ISR Ne(h) profiles. Possible reasons have been investigated including the specific ionogram inversion method applied to Digisonde bottomside profiles that could lead to inaccuracies in the hmF2 calculation. Pretty roughly extrapolated topside Digisonde Ne(h) profiles do not also help in an efficient performance of our method. Therefore, for this application, the topside part of the Ne(h) profiles was approximated using the NeQuick model. As a future step it is planned to investigate also the performance of various topside profilers in respect to measured topside profiles (including FORMOSAT-3/COSMIC radio occultation observations) and to assess the impact of possible inaccuracies to our method.
Acknowledgments
The authors thank the Millstone Hill Group of the Massachusetts Institute of Technology, Westford for running the radar and providing the data and personally L.P. Goncharenko for her help with data loading. The research was supported by the NATO Collaborative Linkage Grant CLG 984141 and the COST Action ES0803.
References
- Banks, P.M., and G. Kockarts, Aeronomy, Academic Press, New York, London, 1973. [Google Scholar]
- Belehaki, A., N. Jakowski, and B.W. Reinisch, Comparison of ionospheric ionization measurements over Athens using ground ionosonde and GPS-derived TEC values, Radio Sci., 38 (6), 1105, 2003. [CrossRef] [Google Scholar]
- Belehaki, A., L.J. Cander, B. Zolesi, J. Bremer, C. Juren, I. Stanislawska, D. Dialetis, and M. Hatzopoulos, Monitoring and forecasting the ionosphere over Europe: The DIAS project, Space Weather, 4, S12002, DOI: 10.1029/2006SW000270, 2006 (S1.1). [CrossRef] [Google Scholar]
- Belehaki, A., I. Kutiev, B. Reinisch, N. Jakowski, P. Marinov, I. Galkin, C. Mayer, I. Tsagouri, and T. Herekakis, Verification of the TSMP-assisted Digisonde (TaD) topside profiling technique, Acta Geophysica, DOI: 10.2478/s11600-009-0052-3, 2009. [Google Scholar]
- Berger, C., R. Biancale, M. Ill, and F. Barlier, Improvement of the empirical thermospheric model DTM: DTM94 – comparative review on various temporal variations and prospects in space geodesy applications, J. Geod., 161, 178, 1998. [Google Scholar]
- Bilitza, B., L. McKinnell, B.W. Reinisch, and T. Fuller-Rowell, The International Reference Ionosphere (IRI) today and in the future, J. Geodesy, DOI: 10.1007/s00190-010-0427-x, 2011. [Google Scholar]
- Bowman, B.R., W.K. Tobiska, F.A. Marcos, C.Y. Huang, C.S. Lin, and W.J. Burke, A new empirical thermospheric density model JB2008 using new solar and geomagnetic indices, AIAA/AAS Astrodynamics Specialist Conference, 18–21 August 2008, Honolulu, Hawaii, 19, 2008. [Google Scholar]
- Bruinsma, S.L., and J.M. Forbes, Anomalous behavior of the thermosphere during solar minimum observed by CHAMP and GRACE, J. Geophys. Res., 115, A11323, DOI: 10.1029/2010JA015605, 2010. [CrossRef] [Google Scholar]
- Bruinsma, S.L., G. Thuillier, and F. Barlier, The DTM-2000 empirical thermosphere model with new data assimilation and constrains at lower boundary: accuracy and properties, J. Atmos. Sol.-Terr. Phys., 65, 1053–1070, 2003. [Google Scholar]
- Bruinsma, S., D. Tamagnan, and R. Biancale, Atmospheric density derived from CHAMP/STAR accelerometer observations, Planet Space Sci., 52, 297–312, 2004. [CrossRef] [Google Scholar]
- Bruinsma, S., J.M. Forbes, R.S. Nerem, and X. Zhang, Thermospheric density response to the 20–21 November 2003 solar and geomagnetic storm from CHAMP and GRACE accelerometer data, J. Geophys. Res., 111, A06303, DOI: 10.1029/2005JA011284, 2006. [CrossRef] [Google Scholar]
- Buonsanto, M.J., D.P. Sipler, G.B. Davenport, and J.M. Holt, Estimation of the O+, O collision frequency from coincident radar and Fabry-Perot observations at Millstone Hill, J. Geophys. Res., 102, 17267–17274, 1997. [CrossRef] [Google Scholar]
- Chen, C.F., B.W. Reinisch, J.L. Scali, X. Huang, R.R. Gamache, M.J. Buonsanto, and B.D. Ward, The accuracy of ionogram-derived N(h) profiles, Adv. Space Res., 14 (12), 43–46, 1994. [Google Scholar]
- Di Giovanni, G., and S.M. Radicella, An analytical model of the electron density profile in the ionosphere, Adv. Space Res., 10, 27, 1990. [Google Scholar]
- Emmert, J.T., and J.M. Picone, Climatology of globally averaged thermospheric mass density, J. Geophys. Res., 115, A09326, DOI: 10.1029/2010JA015298, 2010. [CrossRef] [Google Scholar]
- Galkin, I.A., G.M. Khmyrov, A.V. Kozlov, B.W. Reinisch, X. Huang, and V.V. Paznukhov, The ARTIST 5, Radio Sounding and Plasma Physics, AIP Proceedings, 974, 150–159, 2008. [Google Scholar]
- Hedin, A.E., MSIS-86 thermospheric model, J. Geophys. Res., 92, 4649–4662, 1987. [Google Scholar]
- Himmelblau, D.M., Applied Nonlinear Programming, McGraw-Hill, New York, 1972. [Google Scholar]
- Ivanov-Kholodny, G.S., and A.V. Mikhailov, The Prediction of Ionospheric Conditions, D. Reidel Publishing Company, Dordrecht, Holland, 1986. [Google Scholar]
- Ivanov-Kholodny, G.S., and G.M. Nikoljsky, The Sun and the Ionosphere, Nauka, Moscow, 1969, pp. 455, (in Russian). [Google Scholar]
- Kil, H., Y.-S. Kwak, L.J. Paxton, R.R. Meier, and Y. Zhang, O and N2 disturbances in the F region during the 20 November 2003 storm seen from TIMED/GUVI, J. Geophys. Res., 116, A02314, DOI: 10.1029/2010JA016227, 2011. [CrossRef] [Google Scholar]
- Kutiev, I., P. Marinov, A. Belehaki, B. Reinisch, and N. Jakowski, Reconstruction of topside density profile by using the topside sounder model profiler and Digisonde data, Adv. Space Res., 43 (11), 1683–1687, 2009. [Google Scholar]
- Lathuillère, C., M. Menvielle, A. Marchaudon, and S. Bruinsma, A statistical study of the observed and modeled global thermosphere response to magnetic activity at middle and low latitudes, J. Geophys. Res., 113, A07311, DOI: 10.1029/2007JA012991, 2008. [CrossRef] [Google Scholar]
- Lei, J., W. Wang, A.G. Burns, S.C. Solomon, A.D. Richmond, M. Wiltberger, L.P. Goncharenko, A. Coster, and B.W. Reinisch, Observations and simulations of the ionospheric and thermospheric response to the December 2006 geomagnetic storm: initial phase, J. Geophys. Res., 113, A01314, DOI: 10.1029/2007JA012807, 2008. [CrossRef] [Google Scholar]
- Lei, J., J.P. Thayer, G. Lu, A.G. Burns, W. Wang, E.K. Sutton, and B.A. Emery, Rapid recovery of thermosphere density during the October 2003 geomagnetic storms, J. Geophys. Res., 116, A03306, DOI: 10.1029/2010JA016164, 2011. [CrossRef] [Google Scholar]
- Litvin, A., W.L. Oliver, J.M. Picone, and M.J. Buonsanto, The upper atmosphere during June 5–11, 1991, J. Geophys. Res., 105, 12789–12796, 2000. [CrossRef] [Google Scholar]
- Mikhailov, A.V., and J.C. Foster, Daytime thermosphere above Millstone Hill during severe geomagnetic storms, J. Geophys. Res., 102, 17275–17282, 1997. [CrossRef] [Google Scholar]
- Mikhailov, A.V., and M. Förster, Some F2-layer effects during the January 06–11, 1997 CEDAR storm period as observed with the Millstone Hill incoherent scatter facility, J. Atmos. Sol.-Terr. Phys., 61, 249–261, 1999. [Google Scholar]
- Mikhailov, A.V., and W. Kofman, An interpretation of ion composition diurnal variation deduced from EISCAT observations, Ann Geophysicae, 19, 351–358, 2001. [CrossRef] [Google Scholar]
- Mikhailov, A.V., and J. Lilensten, A revised method to extract thermospheric parameters from incoherent scatter observations, Ann Geophysics, Supp., 47 (N2/3), 985–1008, 2004. [Google Scholar]
- Mikhailov, A.V., and L. Perrone, On the mechanism of seasonal and solar cycle NmF2 variations: A quantitative estimate of the main parameters contribution using incoherent scatter radar observations, J. Geophys. Res., 116, A03319, DOI: 10.1029/2010JA016122, 2011. [CrossRef] [Google Scholar]
- Mikhailov, A.V., and K. Schlegel, Self-consistent modeling of the daytime electron density profile in the ionospheric F-region, Ann. Geophysicae, 15, 314–326, 1997. [Google Scholar]
- Mikhailov, A.V., and K. Schlegel, Geomagnetic storm effects at F1-layer heights from incoherent scatter observations, Ann Geophysicae, 21, 583–596, 2003. [CrossRef] [Google Scholar]
- Munninghoff, D.E., Ion and electron temperatures in the topside ionosphere, in Aeronomy Report 86, Aeronom. Lab. Univ.. Illinois, Urbana, 1979. [Google Scholar]
- Nava, B., P. Coisson, and S.M. Radicella, A new version of the NeQuick ionosphere electron density model, J. Atmos. Sol.-Terr. Phys., 70, 1856–1862, 2008. [Google Scholar]
- Nusinov, A.A., Solar activity dependence of the intensity of shortwave radiation, Geomag. i Aeronom., 24, 529–536, 1984, (in Russian). [Google Scholar]
- Nusinov, A.A., Models for prediction of EUV and X-ray solar radiation based on 10.7-cm radio emission, in Proceedings Workshop on Solar Electromagnetic Radiation for Solar Cycle 22, Boulder, Co., July 1992, ed. R.F., Donnely, NOAA ERL. Boulder, Co, USA, 354–359, 1992. [Google Scholar]
- Oliver, W.L., and K. Glotfelty, O+-O collision cross section and long-term F region O density variations deduced from the ionospheric energy budget, J. Geophys. Res., 101, 21769–21784, 1996. [CrossRef] [Google Scholar]
- Pesnell, W.D., K. Omidvar, and W.R. Hoegy, Momentum transfer collision frequency of O+-O, Geophys. Res. Lett., 20, 1343–1346, 1993. [CrossRef] [Google Scholar]
- Picone, J.M., A.E. Hedin, D.P. Drob, and A.C. Aikin, NRLMSISE-00 empirical model of the atmosphere: Statistical comparison and scientific issues, J. Geophys. Res., 107, 1468, DOI: 10.1029/2002JA009430, 2002. [Google Scholar]
- Prölss, G.W., Physics of the Earth’s Space Environment, Springer-Verlag, Berlin, Heidelberg, 2004, 513. [Google Scholar]
- Prölss, G.W., S. Werner, M.V. Codrescu, T.J. Fuller-Rowell, A.G. Burns, and T.L. Killeen, The thermospheric-ionospheric storm of Dec 8, 1982: Model predictions and observations, Adv. Space Res., 22 (1), 123–128, 1998. [CrossRef] [Google Scholar]
- Radicella, S.M., and R. Leitinger, The evolution of the DGR approach to model electron density profiles, Adv. Space Res., 27 (1), 35–40, 2001. [Google Scholar]
- Reinisch, B.W., and X. Huang, Automatic calculation of electron density profiles from digital ionograms, 3, Processing of bottomside ionograms, Radio Sci., 18, 477–492, 1983. [CrossRef] [Google Scholar]
- Reinisch, B.W., and X. Huang, Deducing topside profiles and total electron content from bottomside ionograms, Adv, Space Res., 27 (1), 23–30, 2001. [Google Scholar]
- Reinisch, B.W., I.A. Galkin, G. Khmyrov, A. Kozlov, and D.F. Kitrosser, Automated collection and dissemination of ionospheric data from the digisonde network, Adv. Radio Sci., 2, 241–247, 2004. [Google Scholar]
- Reinisch, B.W., X. Huang, I.A. Galkin, V. Paznukhov, and A. Kozlov, Recent advances in real-time analysis of ionograms and ionospheric drift measurements with digisondes, J. Atmos. Sol.-Terr. Phys., 67, 1054–1062, 2005. [Google Scholar]
- Reinisch, B.W., P. Nsumei, X. Huang, and D. K. Bilitza, Modeling the F2 topside, plasmasphere for IRI using IMAGE/RPI, ISIS data, Adv. Space Res., 39, 731–738, 2007. [CrossRef] [Google Scholar]
- Reinisch, B.W., P. Nsumei, X. Huang, and D. Bilitza, A new Vary-Chap model of topside electron density profiles based on ISIS-2 sounding data, in Proceedings of the Ionospheric Effects Symposium, A 130, JMG Associates, Ltd., Alexandria, VA, USA, 2011. [Google Scholar]
- Richards, P.G., Reexamination of ionospheric photochemistry, J. Geophys. Res., 116, A08307, DOI: 10.1029/2011JA016613, 2011. [Google Scholar]
- Richards, P.G., and D.G. Torr, Ratios of photoelectron to EUV ionization rates for aeronomic studies, J. Geophys. Res., 93, 4060–4066, 1988. [CrossRef] [Google Scholar]
- Richards, P.G., J.A. Fennelly, and D.G. Torr, EUVAC: A solar EUV flux model for aeronomic calculations, J. Geophys. Res., 99, 8981–8992, 1994. [Google Scholar]
- Richmond, A.D., E.C. Ridley, and R.G. Roble, A thermosphere/ionosphere general circulation model with coupled electrodynamics, Geophys. Res. Lett., 19, 601, 604, 1992. [Google Scholar]
- Torr, M.R., D.G. Torr, R.A. Ong, and H.E. Hinteregger, Ionization frequencies for major thermospheric constituents as a function of solar cycle 21, Geophys. Res. Lett., 6, 771–774, 1979. [NASA ADS] [CrossRef] [Google Scholar]
- Wang, W., M. Wiltberger, A.G. Burns, S.C. Solomon, T.L. Killeen, N. Maruyama, and J.G. Lyon, Initial results from the coupled magnetosphere-ionosphere-thermosphere model: thermosphere-ionosphere responses, J. Atmos. Sol.-Terr. Phys., 66/15–16, 1425, 2004. [Google Scholar]
- Wang, W., A.G. Burns, M. Wiltberger, S.C. Solomon, and T.L. Killeen, Altitude variations of the horizontal thermospheric winds during geomagnetic storms, J. Geophys. Res., 113, A02301, DOI: 10.1029/2007JA012374, 2008. [CrossRef] [Google Scholar]
All Tables
List of input (both measured and model) parameters used in the method and the retrieved ones.
Thermospheric parameters used to calculate Ne(h) in the direct model run and the retrieved from this Ne(h) profile neutral composition, temperature, and wind.
Comparison of MSISE-00 and JB2006 model predictions with CHAMP neutral gas density observations for the periods of solar maximum (October 2002) and solar minimum (February 2008) activity. Standard deviation and mean relative deviation are given, analyzing a total number of 2414 measurements.
Calculated neutral gas density using Digisonde Ne(h) profiles extrapolated with NeQuick for three dates with SAO hmF2 much lower ISR hmF2 values.
Thermospheric parameters variation resulted from Ne(h) shift as a whole by +5 to −20 km. The accuracy Δ of Ne(h) fitting is also given.
All Figures
 |
Fig. 1. Height dependences for vertical plasma drift in magnetically quiet and disturbed conditions. |
| In the text | |
 |
Fig. 2. Determination of Tex. Triangles – Δ and ρ/Δ values obtained in calculations with various Tex. Solid line – the 5th order polynomial approximation. Arrows indicate the extreme positions. Top panels illustrate a “good” case when Tex is found reliably from Δ and ρ/Δ parameters. In the second case (lower panels) the Δ parameter exhibits a plateau in a wide range of temperatures and Tex can be found only from one parameter, ρ/Δ. |
| In the text | |
 |
Fig. 3. Two examples illustrating the quality of the observed Ne(h) profiles fitting with the method. Solid lines – Millstone Hill ISR observed profiles, dashes – the results of calculations. One good and one bad cases of fitting are shown. |
| In the text | |
 |
Fig. 4. The observed daily F10.7, the daily Ap (solid), and 3-hourly ap(dots) indices for the period 4–30 October 2002. Millstone Hill ISR and Digisonde-hmF2 and -NmF2 values, corresponding to local noon observations, are also shown for a comparison. |
| In the text | |
 |
Fig. 5. Reduced to the Millstone Hill location and 400 km height CHAMP neutral gas density observations along with ±10% error bars, MSISE-00 and JB2006 model predictions and the model extracted neutral gas density at 400 km height using ISR Ne(h) profiles. |
| In the text | |
 |
Fig. 6. Same as Figure 4 for January 2008. |
| In the text | |
 |
Fig. 7. Same as Figure 5 but for January 2008. The comparison is made at 340 km. |
| In the text | |
 |
Fig. 8. CHAMP neutral gas density observations, reduced to the location of Millstone Hill, along with ±10% error bars and the model calculated neutral gas density at 400 km height using Digisonde/NeQuick model profiles, for October 2002 (solar maximum). |
| In the text | |
 |
Fig. 9. Same as Figure 8 for January 2008, for solar minimum conditions. The comparison is made at 340 km. |
| In the text | |
 |
Fig. 10. Histograms for CHAMP/model ratios for October 2002 (solar maximum) and February 2008 (solar minimum). MSISE-00 and JB2006 models were used for a comparison. The comparisons were made at 400 km for October 2002 and at 340 km for February 2008. |
| In the text | |
 |
Fig. 11. Observed at Millstone Hill F2-layer maximum parameters along with AE index variations for 13–15 December, 2006. Triangles – Digisonde, circles – ISR observations, dashes – 27-day running medians calculated from Digisonde data. LT = UT-5. |
| In the text | |
 |
Fig. 12. Calculated relative ion composition for the periods of negative and positive F2-layer storms. The standard Millstone Hill ion composition model is given for a comparison. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


