| Issue |
J. Space Weather Space Clim.
Volume 3, 2013
|
|
|---|---|---|
| Article Number | A15 | |
| Number of page(s) | 16 | |
| DOI | https://doi.org/10.1051/swsc/2013038 | |
| Published online | 08 April 2013 | |
Research Article
Retrieval of thermospheric parameters from routinely observed F2-layer Ne(h) profiles at the geomagnetic equator
1
Pushkov Institute of Terrestrial Magnetism, Ionosphere and Radio Wave Propagation (IZMIRAN), Troitsk, Moscow Region 142190, Russia
2
Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing, National Observatory of Athens, Metaxa and Vas. Pavlou, Palaia Penteli, 15236 Greece
3
Istituto Nazionale di Geofisica e Vulcanologia (INGV), Via di Vigna Murata 605, Rome 00143, Italy
* Corresponding author: e-mail: belehaki@noa.gr
A principal possibility to retrieve basic thermospheric parameters (neutral temperature Tex, atomic [O] and molecular [O2] oxygen as well as molecular nitrogen [N2] concentrations) from the observed daytime electron density profiles Ne(h) in the equatorial F2-region is demonstrated for the first time. The reduction of a 2D continuity equation for electron concentration in the low-latitude F2-region at the geomagnetic equator (I = 0) results in a simple 1D equation which can be efficiently solved. The method was tested using Jicamarca Incoherent Scatter Radar (ISR) and Digisonde Ne(h) profiles for the periods when CHAMP and GRACE neutral gas density observations are available in the vicinity of the Jicamarca Observatory. The retrieved from ISR Ne(h) neutral gas densities were shown to be close to the observed ones (MRD < 10%) being within the announced absolute uncertainty (10–15%) of the neutral gas density observations and more successful than the predictions of the empirical models JB-2008 (MRD = 32%) and MSISE-00 (MRD = 27%) for the analyzed cases. The implementation of the method with Jicamarca Digisonde Ne(h) profiles has also shown acceptable results especially for solar minimum conditions (MRD ~ 12%) and higher prediction accuracy than modern empirical models provide. This finding seems to open a way for the practical exploitation of the method for thermospheric monitoring purposes.
Key words: thermosphere / ionosphere (equatorial) / modelling / drag / monitoring
© A. Mikhailov et al., Published by EDP Sciences 2013
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0) which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0) which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
In a recent paper (Mikhailov et al. 2012, further M2012) we discussed the need for developing methods for monitoring the thermosphere in support of satellite constellations orbiting in the near-Earth geospace that support critical operations such as navigation, surveillance, and communication. In practice, the development of such a method meets many difficulties since neither empirical (statistical) models nor global first-principle (physical) models can efficiently simulate the actual situation, especially under disturbed conditions due to the complexity of the Earth’s upper atmosphere dynamics. However, such conditions are the most important and interesting ones from the practical point of view. This is the reason why we proposed an alternative approach in monitoring the thermospheric conditions, which is based on quite different principles (M2012). More precisely, the Earth’s ionosphere is embedded in the neutral thermosphere (even in the F2-layer maximum the ion-to-neutrals ratio is ~10−3) and it closely follows the state of the thermosphere at least during sunlit hours. Therefore the ionosphere may serve as an indicator of the state of the thermosphere under various geophysical conditions, and one may consider the possibility to extract thermospheric parameters from ionospheric observations for thermospheric monitoring purposes. The idea sounds promising, especially if one takes into account that there are many Digisondes installed over the world which work on a regular basis and the ionospheric observations are available via Internet practically in real time.
The M2012 method for middle latitudes retrieves thermospheric neutral composition and temperature from electron density Ne(h) profiles from Millstone Hill Incoherent Scatter Radar (ISR) and Digisonde for daytime hours. CHAMP neutral gas density observations obtained both under solar maximum (October 2002) and minimum (January 2008) activity were used for the verification of the proposed method. The retrieved gas densities lay in the ±(10–15)% corridor around the observed ones, which corresponds to the announced absolute accuracy of CHAMP observations, provided that Ne(h) ISR profiles were used for the retrieval. On the other hand, the exploitation of routine Digisonde Ne(h) profiles in the proposed method has been proven to be not a straightforward task, since when these were used for the retrieval, the performance of the method was degraded especially under solar minimum conditions. The detected weaknesses were attributed to uncertainties in the hmF2 and the topside Ne(h) model-estimates provided routinely by Digisondes. Our findings indicate that most probably the routine Digisonde Ne(h) profiles available at middle latitudes should be subject to special analysis before their efficient exploitation by the proposed method (M2012). These are certain limitations in using Digisonde Ne(h) and have to be carefully worked out in the future.
The present paper is an attempt to apply the method at the geomagnetic equator where Jicamarca ISR radar and Digisonde observations are available for the period of CHAMP and GRACE functioning. The region of the geomagnetic equator was selected for testing the method because the ISR facility and the Digisonde are almost co-located, making possible the comparative analysis of the results. Another reason lies in the special form of the continuity equation for the electron concentration which can be used in the vicinity of the geomagnetic equator (see Appendix 1). This is a first-order equation which needs only one boundary condition for its solution, simplifying the requirements to the input Ne(h) profiles.
In this paper we concentrate on the following tasks:
-
to develop a method that extracts basic thermospheric parameters from Ne(h) profiles observed at the geomagnetic equator,
-
to calculate the neutral gas density using Ne(h) profiles and compare the calculations with available CHAMP and GRACE neutral gas density observations under various geophysical conditions,
-
to investigate the limitations of this method, especially concerning the use of routine Digisonde Ne(h) profiles.
2. Description of the method
For the convenience of the reader we will give the main idea of the M2012 method pointing out the differences related to the specificities of using the method at the geomagnetic equator. Similar to the middle-latitudes case, only sunlit conditions are considered. The roles of the different atmospheric species are more distinct under the influence of the ionizing solar EUV radiation and this should help their separation solving the inverse problem of aeronomy.
2.1. Ionospheric model
The ionospheric model is used as a tool in our method to split the observed Ne(h) profile into the aeronomic parameters responsible for this Ne(h) distribution. This tool should be simple as much as possible to be an operative one, but should also take into account the main processes that are responsible for the formation of the daytime F2-layer at the geomagnetic equator. The list of the main processes is well known: (a) photo-ionization of neutral [O], [O2], [N2] species by solar EUV, (b) vertical plasma transfer by ExB drift and its diffusion apart from the equator, and (c) plasma recombination in the chain of ion-molecular reactions. Vertical plasma transfer by neutral winds is inefficient at the geomagnetic equator where the magnetic inclination I = 0. During daytime hours it is also possible to neglect the effects of the zonal ExB plasma transfer in a comparison with the vertical one. Therefore our tool includes transport process for O+(4S) and photo-chemical processes only for O+(2D), O+(2P), O2+(X2П), N+, N2+, and NO+ ions in the 170–650 km height range. A two-component model of the solar EUV from Nusinov (1984, 1992) is used to calculate photo-ionization rates in 48-wavelength intervals (10–1050) Å. The photo-ionization and photo-absorption cross-sections are obtained from Torr et al. (1979), Richards & Torr (1988), Richards et al. (1994) and from Ivanov-Kholodny & Nikoljsky (1969) for X-ray emission. The list of chemical processes used in the scheme is given in reference Mikhailov & Lilensten (2004). More recent chemical reaction rate constants may be found, for instance, in reference Richards (2011).
The concentration of the O+(4S) ions is calculated from the continuity equation: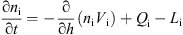 which at the geomagnetic equator (see Appendix 1) may be written as follows:
which at the geomagnetic equator (see Appendix 1) may be written as follows:![$$ \frac{\mathrm{\partial }n}{\mathrm{\partial }t}+\left(\frac{2{D}_{\mathrm{a}}}{r}+W\right)\frac{\mathrm{\partial }n}{\mathrm{\partial }r}+\left[\frac{2{D}_{\mathrm{a}}}{r}\left(\frac{\mathrm{\partial }\mathrm{ln}{T}_{\mathrm{p}}}{\mathrm{\partial }r}+\frac{1}{{H}_{\mathrm{p}}}\right)+\frac{6W}{r}+R\right]n=Q, $$](/articles/swsc/full_html/2013/01/swsc120060/swsc120060-eq2.gif) (1)where Da – ambipolar diffusion coefficient (Banks & Kockarts 1973), r – geocentric distance, W – vertical E × B plasma drift velocity, Tp = Te + Ti –plasma temperature, Hp = kTp/mg – plasma scale height, R = γ1[N2]+ γ2[O2] – linear loss coefficient, Q – O+ production rate due to the solar EUV ionization.
(1)where Da – ambipolar diffusion coefficient (Banks & Kockarts 1973), r – geocentric distance, W – vertical E × B plasma drift velocity, Tp = Te + Ti –plasma temperature, Hp = kTp/mg – plasma scale height, R = γ1[N2]+ γ2[O2] – linear loss coefficient, Q – O+ production rate due to the solar EUV ionization.
Equation (1) was obtained by Deminov et al. (1977). The comparison of this equation with a two-dimensional continuity equation for the electron concentration usually used to describe the equatorial F2-layer has shown that it may be used to model the observed Ne(h) distribution up to ~500–600 km height (Leschinskaya & Mikhailov 1984). The effect of plasma flow away from the geomagnetic equator along magnetic field lines is taken into account in (1) by the terms with 2Da/r and 6W/r.
Equation (1) is of a hyperbolic type of the first order and it requires only one boundary condition for its solution. In our case this is the lower boundary condition at 180–190 km where [O+] is supposed to be in the photo-chemical equilibrium. The upper boundary at ~600 km is free and this is convenient from the practical point of view keeping in mind the limitations in the model’s performance at middle latitudes that come from the uncertainties in the Digisonde Ne(h) extrapolation in the topside ionosphere. This was one of the problems mentioned in M2012 as at middle latitudes the continuity equation is of the second order and needs the specification of the upper boundary condition for its solution.
2.2. The energy balance equation
Similar to the middle-latitude case (M2012), electron and ion temperatures are not the parameters of our main interest, but they are used in the continuity Eq. (1) and therefore they should be specified. Vertical heat transfer is absent at the geomagnetic equator due to I = 0 and for this reason Te(h) and Ti(h) manifest a specific height distribution. An example is shown in Figure 1 with Jicamarca ISR daytime observations under low (April, 2006) and moderate (December, 2004) solar activity.
 |
Fig. 1. Daytime Te (solid) and Ti (dashes) profiles observed with Jicamarca ISR, where LT = UT-5. |
The pronounced peak of the electron temperature around 200 km is due to local heating by the solar EUV radiation. In the 300–500 km height range Te is ~20% larger than Ti. Above ~500 km height, Te starts to increase and this increase is more pronounced for higher solar activity. This increase in the electron temperature is a projection of the low-middle latitude Te values along the magnetic field lines to the equatorial plane. Of course, in our 1D consideration we cannot take into account this 2D feature. For this reason, we have confined ourselves with local EUV heating to describe the main Te peak up to ~250 km, while for higher altitudes we use some approximations to mimic the observed type of Te(h) variations. An accurate description of the Te and Ti distributions in the low-latitude topside ionosphere is a complicated problem (e.g., Varney et al. 2011) which is outside the scope of the present analysis.
The EUV heating rate may be specified as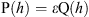 (2)where ε is the heating efficiency and Q is the total photo-ionization rate, with ε being a fitting parameter in our method. Depending on the (Te-Ti) and (Te-Tn) sign some processes may work as heating or cooling the electron gas and they are prescribed to the corresponding terms in the energy balance equation. The expressions for electron cooling processes can be found in references Banks & Kockarts (1973) and Munninghoff (1979).
(2)where ε is the heating efficiency and Q is the total photo-ionization rate, with ε being a fitting parameter in our method. Depending on the (Te-Ti) and (Te-Tn) sign some processes may work as heating or cooling the electron gas and they are prescribed to the corresponding terms in the energy balance equation. The expressions for electron cooling processes can be found in references Banks & Kockarts (1973) and Munninghoff (1979).
Equating the ion thermal energy input from electron-ion collision to that lost through collisions with neutral particles, an approximate expression for the ion temperature can be obtained ignoring thermal conduction (Banks & Kockarts 1973):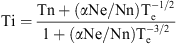 (3)where α ≈ 6 × 106 and Nn is the neutral gas number density.
(3)where α ≈ 6 × 106 and Nn is the neutral gas number density.
2.3. Retrieved parameters
The principles adopted for the selection of the retrieved aeronomic parameters were discussed in M2012. Keeping in mind the specificities of the equatorial F2-layer, the list of these parameters is slightly different from the middle-latitude one and includes: exospheric temperature Tex, factors for the MSIS-86 (Hedin 1987) model [O], [O2], [N2] concentrations, vertical ExB plasma drift W, a factor for the Nusinov (1984, 1992) model of the total solar EUV flux with λ < 1050 Å, and ε – heating efficiency to calculate the electron temperature. Daytime equatorial F2-layer is located at heights larger than 200 km, therefore neutral temperature at 120 km and the shape parameters S specifying Tn(h) profile below 200 km are not very important and are taken from the MSIS-86 (Hedin 1987) model. Vertical E × B plasma drift W is practically height independent (Balsley et al. 1976; Fejer 1981; Kudeki et al. 1999) and this simplifies the calculations. The extraction of thermosphere parameters from ionospheric ones is a problem of nonlinear programming (Himmelblau 1972).
2.4. Fitting procedure
The fitting procedure has been slightly changed comparing to the middle-latitude version. Only the bottom-side Ne(h) profile is fitted and a large weight is given to the NmF2. The latter should guarantee coincidence between the observed and the calculated NmF2, while hmF2 may not coincide with the observed one. This new element introduced into the fitting procedure may turn out to be efficient as NmF2 is the most reliably observed parameter while significant uncertainty takes place with respect to the hmF2. The process starts with searching for Tex. Exospheric temperature is the key parameter which cannot be found along with the other parameters within one algorithm and a special method has been developed for its determination. The method is running for various Tex in a wide range of Tex values with a large step of 10 K. We are checking Tex in the area ±(100–150) K around the MSIS-86 Tex value. On one hand MSIS itself takes into account the disturbance in Tex and we work around this disturbed Tex value, on the other hand we may extend this interval say up to ±(300–400) K, but in reality there is no need in such wide intervals for Tex searching. Having 2–3 model (MSIS-86, MSISE-00, JB-2008) values of Tex for the condition in question we know the temperature interval for searching of Tex.
The quality of Ne(h) fitting depends on Tex and normally the global minimum exists in delta specified as: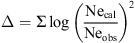 (4)
(4)
Only the bottom-side of the Ne(h) profile is used to calculate Δ. If the global minimum exists in the Δ variations, then the method is run again with a small step (1–2) K in the area of the minimum to specify the final Tex value (Fig. 2, top panel). The absence of the global minimum in the Δ variations tells us that no solution exists under the selected constraints (see later). There are two types of the Δ dependence: with one and two minima, in both cases the global minimum should be found. Two examples are given in Figure 2 for July 08 and July 13, 2008.
 |
Fig. 2. Calculated Δ (see expression 4) variations to find Tex in the global minimum. Two types of Δ variations are given: with one and two minima, in any case the global minimum should be found. Calculated (dashes) with these Tex and observed (solid) Ne(h) profiles are shown. |
In reality the situation is more complicated. The Δ dependence is not smooth and manifests many local minima. For this reason a 5th degree polynomial approximation is applied to the Δ dependence and the smoothed curve indicates the position of the global minimum. The process of searching for the solution is complicated due to the dependence on the constraining intervals chosen for each variable. If these intervals are poorly selected, no solution can be found at all in the range of the physically accepted values for Tex, while the method is not efficient if wide intervals are selected for the variables. Lots of tests were required to specify these constraints for each variable. For instance, the constraining intervals are different for each of the neutral species. Normally the interval is ±20% (factors 0.8–1.2) around the MSIS-86 model [O] values. But atomic oxygen is known to be a very variable constituent of the upper atmosphere, and for this reason an additional constraining interval (factors 0.4–1.0) with respect to the MSIS-86 concentration is tested for atomic oxygen in each case. The fixed constraining intervals were selected for [N2] (factors 0.6–1.2) and for [O2] (factors 0.3–0.9) with respect to the MSIS-86 concentrations. There are four constraining intervals for the vertical drift in the (−20 ÷ +70) m/s range and all four intervals should be tested to select the solution. Therefore this is a very time-consuming procedure which requires lots of calculations.
The basic idea to select the solution is the following. When neutral gas density is known, for instance from CHAMP observations, the solution is selected easily. The global minimum in the Δ dependence corresponds to its own neutral gas density. The run that provides the best coincidence with the observed neutral gas density in the Δ global minimum is considered as the solution. However, when we work “blindly” without neutral gas density observations (a real situation) it is difficult to choose the solution among various versions of calculations. The best Ne(h) fitting (the least Δ) does not necessarily correspond to the solution, since the observed Ne(h) profile may be not accurate enough, but the method can fit it as well. The best fit may be also obtained under unreal Tex or vertical plasma drift values. Therefore the results should be analyzed from the point of view of their reasonability keeping in mind the geophysical conditions in question.
The following practical method was used to select the solution. Along with Δ, we calculate the R = ρ/Δ ratio. After polynomial smoothing of ρ/Δ we specify the R value in the Δ(Tex) global minimum for all versions of calculations. The analysis has shown that usually the solution is among those runs for which R values are the largest. If two-three of the largest R values manifest very different vertical plasma drifts, then the priority is given to that one for which the drift is the least. If all calculated drifts are reasonable from physical point of view (Fejer & Scherliess 1997; Scherliess & Fejer 1999; Fejer et al. 2008; Stoneback et al. 2011), then the run with the least Δ (among two-three with the largest R values) is taken as the solution. An example how to select the solution is given in Table 1.
Selection of the solution for September 12, 2007 (~2000 UT). A non-stationary method is compared to a stationary one for several versions of calculations (see text). The minimal Δ and the corresponding neutral gas density ρ, exospheric temperature Tex, vertical plasma drift W, and ρ/Δ are given. Three maximal ρ/Δ and the corresponding ρ values are given in bold.
There are both stationary and non-stationary versions of the method. In the case of a non-stationary solution, the height profile of O+ ions from the previous time step should be specified. We consider the heights larger than 200 km where [O+] ≈ Ne, therefore the observed Ne(h) from the previous time step can be used in the non-stationary scheme.
Both stationary and non-stationary methods were used in testing the method. In some cases both solutions exist and the best (according to our criteria) is chosen as the final one. In other cases only one (stationary or non-stationary) solution exists, while sometimes no solution can be found at all. This is seen in the absence of the global minimum in the Δ dependence in the range of the reasonable neutral temperatures. The exact reason for this is not known at present, but some peculiarities of the observed Ne(h) profiles seem to be a reasonable explanation. In such cases, the neighboring in time Ne(h) profile may give a solution. All this indicates that the method is very sensitive in the quality of the observed Ne(h) profiles and at the present stage it is rather an art than a routine procedure. However, as it is shown later, acceptable and reasonable results can be obtained.
A comparison between stationary and non-stationary schemes is given in Table 1 for September 12, 2007, where various versions (Vmn) of calculation are presented for a comparison. The first index “m” indicates the constraining interval for vertical drift, and the second index “n” – the constraining interval for atomic oxygen. For instance, V42 means the (20–40) m/s interval for vertical drift and the (factor 0.4–0.9) interval for atomic oxygen concentration with respect to MSIS-86 model.
The non-stationary method seems to provide better fitting (smaller Δ values) in this case and correspondingly, larger ρ/Δ values as the retrieved neutral gas densities are similar in the two calculation modes. According to our criteria, we should select the largest ρ/Δ values corresponding to V32, V42, and V52 runs. The priority should be given to the V32 version with the least Δ and the lower vertical plasma drift velocity. In the vicinity of the Δ global minimum one should find the temperature Tex which corresponds to the local minimal Δ value. This Tex is used for the final run to give ρ = 2.59 × 10−15 g cm−3, which is close to CHAMP observations reduced to 350 km height: ρ = 2.86 × 10−15 g cm−3. Note that such solution (V51) almost equal to the observed ρ value also exists but we do not adopt it as it does not match our rules for the solution selection. The calculated temperatures are close in the selected cases being also close to the model values Tex = 797 K (Bowman et al. 2008) and Tex = 795 K (Picone et al. 2002). September 12, 2007 was a very quiet day with Ap = 2, so a moderate drift W = 25 m/s (V32 case) seems to be more realistic than W = 32 m/s in the V42 version. On the other hand, E × B drifts are well known to be very variable, so both values may be considered as reasonable.
3. Data
3.1. Input parameters
Following the description of the method in the section above, we summarize in Table 2 the list of the input parameters. The list includes indices of solar and geomagnetic activity: F10.7 for current and previous days as well as the 81-day running mean F10.7 value, a background F10.7 value used in the solar EUV model by Nusinov (1992), and daily Ap index used in the MSIS-86 model. The background F10.7 is a smooth varying function with values changing from ~65 under solar minimum up to ~120 under solar maximum (Nusinov 1984).
List of input parameters used in the method.
The main input parameter is the observed Ne(h) profile. We can acquire Ne(h) profiles from two different sources: ISR and Digisondes. In order to test the performance of our method in low latitudes, we use as a test site Jicamarca, where an ISR and a Digisonde sounder are co-located and therefore the comparison of the results will guide us to determine advantages and limitations in using each type of Ne(h) profile. Jicamarca Observatory is located at 12.0 S; 283.3 E (Ф = −0.57). The ISR works episodically and the observations are available from http://madrigal.haystack.mit.edu/madrigal/. ISR Ne(h) daytime observations cover the ~(170–1000) km range with a ~15 km height step. A 5-degree polynomial smoothing was applied to the initial Ne(h) just to delete small fluctuations as the profiles should be smooth to be used with the method.
The Digisonde in Jicamarca performs one sounding every 15 min as most of the Digisondes, and the data are available from the Lowell DIDBase through GIRO (Reinisch et al. 2004a). It is well known that Digisondes perform measurements only for the bottom part of the ionosphere up to the height of the maximum concentration (hmF2). ARTIST software (Reinisch & Huang 1983; Reinisch et al. 2005; Galkin et al. 2008) makes the ionogram inversion and delivers the Ne(h) profile up to hmF2. Reinisch & Huang (2001) have developed and implemented a Digisonde built-in software that extrapolates the bottomside profile and delivers the Ne(h) profile up to the topside heights. The profile above the peak is approximated by an α-Chapman function with a constant scale height equal to the scale height at the F2 peak.
While in the middle-latitude case the full Ne(h) profile was used as input to M2012, for the low-latitude implementation of the method presented here only the bottomside Ne(h) profile is exploited.
3.2. Data used for the verification of the method
To verify the results of the proposed method, we compare the neutral density values calculated using both types of Ne(h) with in situ satellite observations from CHAMP/STAR and GRACE/SuperSTAR experiments. Overall we have identified 18 daytime coincidences in the vicinity of the Jicamarca Observatory (Table 3).
The contribution (%) of [He] to the total model (MSISE-00 and IB-2008) neutral gas density at the reduction heights, hred, (see text) for the cases of coincidences between observations at Jicamarca site and CHAMP (or GRACE) observations. All neutral gas densities are given in 10−15 g cm−3 units. The cases of largest [He] contribution are given in bold. LT = UT-5.
Detailed information on neutral density space observations as well as the accuracy estimates can be found in Bruinsma et al. (2004, 2006). For our comparison two issues are important: (i) what is the uncertainty in the observed absolute density and (ii) how much is the contribution of He to the total neutral density at heights of the comparison. The latter is important as we retrieve only [O], [O2], and [N2] concentrations, but the observed neutral density includes [He] as well. For CHAMP observations “the total uncertainty in the absolute density value is at the 10–15% level for up to moderate geomagnetic activity conditions (αp = 15)” (Bruinsma et al. 2004). The majority of the cases considered here are under such conditions (Table 5). We could not find similarly clear information about the accuracy for GRACE observations, but one may think that it is not worse than the accuracy of CHAMP measurements, as this follows from the analysis conducted by Bruinsma et al. (2006). Sutton (2008) in his thesis (page 43) reports: “The following sections explain the finer details of processing density and winds from accelerometer measurements from the CHAMP satellite. These methods can be readily applied to other missions, such as GRACE” (page 12), and further: “In the context of our treatment of errors, density estimates are accurate to better than 11% on average”.
CHAMP and GRACE neutral gas density observations which are used in this paper were downloaded from http://sisko.colorado.edu/sutton/data.html. The observed neutral densities in the vicinity of Jicamarca were reduced to the location of the ISR and Digisonde facilities using the MSISE-00 (Picone et al. 2002) thermospheric model and the following expression:
The height for the reduction was selected to be close (<5 km difference) to the satellite height to minimize possible errors due to the MSISE-00 imperfectness. The satellite orbit with available observations was considered as a “close” one to Jicamarca if Δλ ≤ 5o (20 min in LT).
An important issue to be considered in order to obtain meaningful results from this comparison is how the retrieved neutral gas densities can be corrected for [He]. This species is absent from our calculations, and therefore any comparison between observed and model values may not be consistent. The contribution of He to the total density is not essential (see calculations presented in Table 3) under high solar activity and at the height of CHAMP satellite (heights ≤ 400 km), i.e., it is much less than the uncertainty in ρ observations we are working with. But this contribution may be noticeable under solar minimum and for GRACE observations whose orbit is ~100 km higher than the orbit of CHAMP. Therefore the retrieved ρ values are corrected using the model ratio ρtot/ρtot-He at the height of a comparison. We could confine ourselves with the MSISE00 empirical model where all neutral species concentrations are the output parameters. But some model comparisons with CHAMP and GRACE neutral densities have shown the advantages of the JB2008 model over MSISE (Bowman et al. 2008, their Fig. 10; Shim et al. 2012; Mikhailov et al. 2012) and it would be interesting to estimate the [He] contribution to the total neutral density with the JB2008 model as well. The JB2008 model is known to give only neutral temperature and density height profiles. Therefore the model neutral gas density should be split by individual neutral species [O], [O2], [N2], and [He]. This can be done supposing a barometric height distribution for individual species (see Appendix 2). The contribution of [He] to the total model (MSISE-00 and IB-2008) neutral gas density at the reduction heights is given in Table 3 for the cases of simultaneous Jicamarca ISR and CHAMP (or GRACE) observations.
The analysis of Table 3 shows that the contribution of [He] to the total neutral gas density is small in the majority of the cases, in particular when it is calculated with the JB-2008 model. Anyway this contribution is less than the uncertainty in the neutral gas density observations (10–15)% that we are working with. Naturally, the largest contribution takes place for GRACE observations and under low solar activity. The dates with the largest [He] contribution are the same for both thermospheric models. This tells us that the method of splitting the JB-2008 model seems to give reasonable results, although the contribution of [He] is less in the JB-2008 model compared to MSISE-00. To correct our retrieved ρ values for [He], we took the average of the two modeled [He] contributions from Table 3 and added it to the retrieved ρ values. This correction is not large and it is not crucial for the comparison between the observations and the empirical models.
4. Results and first verification attempts
4.1. Testing of the method with ISR Ne(h)
In the case of Jicamarca ISR, two neighboring profiles separated by 10–12 min are used in the non-stationary scheme. But this is not that straightforward in the stationary scheme. Formally a median Ne(h) obtained over (1.0–1.5) h time interval should be used in this case, but such observations may not be available to construct the median Ne(h), for instance, ISR observations may stop any time. For this reason a possibility to use one standing alone Ne(h) profile was examined. A priori it is not clear if the stationary scheme is efficient when F2-region is not stable and F2-layer maximum parameters manifest strong variations. The efficiency was tested during two specially chosen dates with strong hmF2 variations that are given in Figure 3.
 |
Fig. 3. Two dates with strong hmF2 variations. Arrows close to the moment of CHAMP passage over Jicamarca indicate UT moment with ISR Ne(h) observations used in the stationary scheme. |
Both days look unstable and demonstrate large hmF2 variations while NmF2 variations are less intense. More detailed analysis has shown that the large hmF2 variations are due to the Ne(h) bifurcation (splitting) in the vicinity of the F2-layer maximum rather than a real shift of the layer as a whole, which can be seen in the moderate NmF2 variations. So the observed large and fast variations of hmF2 hardly reflect the thermospheric variations. Both stationary and non-stationary calculations were performed to check this. The quality of the Ne(h) fitting with the two methods can be seen in Figure 4 for Mach 24, 2009 and October 29, 2008.
 |
Fig. 4. Fitting of the ISR observed Ne(h) profiles using a non-stationary and a stationary scheme for the periods with strong hmF2 variations (Fig. 3). Observed (solid) and calculated (dashes) Ne(h) profiles are given. |
Figure 4 shows that a non-stationary scheme provides better Ne(h) fitting in the topside, while the bottom-side is fitted well with both methods. The calculated thermospheric parameters are given in Table 4.
Calculated thermospheric parameters for October 29, 2008 and March 24, 2009 using non-stationary and stationary methods. The concentrations are given at 300 km, while ρ is given at 330 km for October and at 320 km for March cases for a comparison with MSISE-00 and CHAMP neutral gas densities.
Both methods are seen to provide similar neutral species concentrations for the March 24 case, with the calculated neutral gas densities being within 2–8% with respect to the CHAMP observations. For the October 29 case, which is magnetically disturbed day, the agreement between the two methods results is worse: 7% in [O], 70% in [O2], 53% in [N2], 50 K in Tex resulting in a 16% difference in ρ. The comparison with CHAMP observations shows that the stationary method underestimates ρ by 16% mainly due to low Tex, when MSISE-00 overestimates neutral gas density by 28% in this case. Summarizing it is possible to conclude that the stationary method being used with an Ne(h) profile observed for a particular UT moment may give acceptable results. Our further testing of the stationary method seems to support this conclusion.
Overall 18 cases of simultaneous ISR and CHAMP (or GRACE) daytime observations were found. Unfortunately, ISR observations may stop earlier or start later than the satellite appears in the vicinity of Jicamarca. However, we have used such satellite observations as well due to a very limited number of the cases available; observed neutral densities were reduced to the nearest in time ISR observations using the MSISE-00 model. In three cases this time difference was up to 3–4 hours.
Calculations for each coincidence case are presented in Table 5, which provides the retrieved and corrected for the [He] contribution neutral densities along with the reduced CHAMP and GRACE observations in comparison with the JB-2008 and MSISE-00 model values. We have checked both stationary and non-stationary schemes and selected the best solution (according to our criteria) among all versions of calculations. As it was mentioned earlier for unknown reasons only one stationary/non-stationary solution may exist. We repeat once again that the absence of a solution means the absence of the global minimum in the Δ dependence.
Dates of available simultaneous Jicamarca ISR and CHAMP or GRACE neutral gas density observations. Observed and reduced to the heights hred neutral gas densities (10−15 g cm−3) are shown in a comparison with the calculated and model values. Calculated ρ values are corrected for the [He] contribution (see text). Daily F10.7 and Ap indices are given. LT = UT-5.
Table 5 shows that both quiet and moderately disturbed periods were analyzed, but the majority of cases are under solar minimum. For a quick visual inspection, neutral gas densities from Table 5 are given in a logarithmic scale in Figure 5.
 |
Fig. 5. A comparison between the retrieved from ISR Ne(h) profiles neutral gas densities with CHAMP and GRACE observations. JB-2008 and MSISE-00 model values are also given for comparison purposes. |
Figure 5 and Table 5 show that the retrieved neutral gas densities are close to the observed ones. Some observations (e.g., July 08 and 09, 2008) manifest very low ρ ~ 1.7 × 10−15 g cm−3, which are much less than the models’ values (2.5–3.2) × 10−15 g cm−3. However, the retrieved neutral gas densities are close to the observed values as the peculiarity of these two days is reflected in the Ne(h) profiles. Some statistical characteristics (SD and mean relative deviation MRD with respect to the observed values) may be also useful for a comparison with the empirical models. The proposed method gives SD = 0.39 g cm−3 and MRD = 8.7%; JB-2008 model gives SD = 0.75 g cm−3 and MRD = 32%; MSISE-00 model gives SD = 0.69 g cm−3 and MRD = 27%. The results of this analysis demonstrate that the proposed method can give acceptable results when ISR Ne(h) profiles are used.
4.2. Testing of the method with Digisonde Ne(h)
As it was mentioned earlier, available ISR data are not numerous and they do not perform systematically, therefore it is important to check the possibility to use the method with routine Digisonde Ne(h). Jicamarca Digisonde 15-min autoscaled Ne(h) profiles were selected for the periods of CHAMP daytime passes over Jicamarca. Unlike ISR, there are enough Digisonde observations coinciding in time with CHAMP passes to provide sufficient evidence for the purposes of the current investigation and therefore GRACE measurements were not used in this part of the analysis. In principle, Digisonde 15-min observations can be used in non-stationary runs of the method. In the case of searching for a stationary solution, the same scheme is used with iterations until a stable solution is obtained. Normally, a median Ne(h) profile calculated over a (1.0–1.5) hour time interval (which is close to e-fold time in the daytime F2-layer) should be used with the stationary scheme, but on one hand such profiles may not be available to calculate the median Ne(h) profile, and on the other hand the method is supposed to be tested in a future work with the COSMIC/FORMOSAT-3 radio-occultation standing alone Ne(h) profiles. For this reason, the instantaneously observed Ne(h) profiles were used to test the stationary scheme.
The method was tested both for solar minimum (2007–2008) and solar maximum (2001–2002) conditions. Data preparation and the method of calculations were the same as earlier with ISR Ne(h) profiles. Table 6 gives the tested periods and the results for solar minimum conditions. The retrieved gas densities were corrected for the [He] contribution (see earlier), although this correction is very small (1.6–2.5)% at (330–360) km altitude under solar minimum conditions. The stationary scheme was used for this testing. JB-2008 and MSISE-00 model values are given for comparison. The testing period was during the last prolonged solar minimum with very low F10.7 and quiet geomagnetic conditions for the majority of the cases. However, disturbed conditions are also included in the list. A comparison between the calculated and the modeled neutral gas densities with the observed ones gave the following statistical results. For our calculations: SD = 0.39 g cm−3 and MRD = 12%; for the JB-2008 model: SD = 0.48 g cm−3 and MRD = 27%; for the MSISE-00 model: SD = 0.54 g cm−3 and MRD = 39%.
Dates of simultaneous Jicamarca Digisonde and CHAMP neutral gas density observations for the period of solar minimum. Observed and reduced to the heights hred neutral gas densities (10−15 g cm−3) are shown in comparison with the calculated and empirical models’ values. Calculated with the stationary scheme ρ values are corrected for the [He] contribution (see text). Daily F10.7 and Ap indices are given. LT = UT-5.
A comparison with ISR results (Table 5) shows comparable performance of the method in both cases. The Digisonde-profile obtained results still lie within the declared inaccuracy of CHAMP neutral gas density observations, while both empirical models demonstrate systematically poorer performance. This is rather expected taking into account that both models do not include the observations during the last deep solar minimum. To facilitate visual inspection of the results, Figure 6 gives a comparison of the retrieved and model neutral gas densities with CHAMP observations.
 |
Fig. 6. A comparison of the JB-2008 and MSISE-00 model values (top) and the calculated using Digisonde Ne(h) profiles (bottom) neutral gas densities with CHAMP observations. |
Figure 6 shows that the retrieved gas densities are more centered with respect to the observed ones while models’ values seem biased overestimating the observed values. The undertaken test has shown that the proposed method provides also acceptable results with Digisonde autoscaled Ne(h) profiles observed under solar minimum conditions. The obtained results are better than the ones provided by the empirical JB-2008 and MSISE-00 models and this result may be interesting from the practical point of view.
Similar tests were performed for solar maximum conditions. As the results obtained with the stationary scheme turned out to be not very good in this case, an additional test was done using the non-stationary scheme. The results are given in Table 7. No non-stationary solution could be obtained for September 14, 2002 (dashes in Table 7).
Dates of simultaneous Jicamarca Digisonde and CHAMP neutral gas density observations for the period of solar maximum. Observed and reduced to the heights hred neutral gas densities (10−15 g cm−3) are shown in comparison with the calculated and model values for solar maximum conditions. Both stationary (ST) and non-stationary (NST) results are presented. Daily F10.7 and Ap indices are given in the last two columns. Dashes on September 14, 2002 mean that no solution was found in that particular coincidence. LT = UT-5.
The statistical results presented in Table 8 indicate that in general the performance of the method is degraded for solar maximum conditions when we use Digisonde autoscaled Ne(h) profiles as input. In this case, the results indicate poorer performance of the method in respect with JB-2008, but a comparable one with MSISE-00.
The SD and MRD statistical parameters comparing calculated and modeled neutral gas densities with CHAMP observations. Stationary and non-stationary results are also compared.
The comparison of the results obtained in the two testing approaches – using Ne(h) profiles from ISR and from Digisondes as input – reveals a tendency for poorer performance of the method in the Digisonde case and especially during solar maximum conditions. As a possible explanation one may consider the fact that the two instruments apply different observing techniques. This results in different intrinsic uncertainties in the measurements and consequently in discrepancies between the observed parameters as it was discussed by Lilensten et al. (2005). Another issue may be the performance of the automatic ionogram scaling and inversion technique applied in Digisondes.
In general, comparisons between Jicamarca Digisonde Ne(h) profiles with COSMIC radio-occultation observations (Chuo et al. 2011) and CHAMP in situ electron density measurements (McNamara et al. 2007) indicate high accuracy for the manually scaled Digisonde Ne(h) profiles. In particular, the comparison made by McNamara et al. (2007) between Jicamarca Digisonde and CHAMP in situ plasma frequency observations for high solar activity conditions (from September 2001 to August 2002) shows that for satellite altitudes below the peak of the F2-layer, the average discrepancy between the two observations is 0.25 MHz or 4%. Nevertheless, autoscaling results depend critically on the quality of the ionograms and the autoscaling algorithm to such extent that indiscriminate use of autoscaled values is not recommended (Reinisch et al. 2004b). Moreover, the visual inspection of the autoscaled profiles used in our cases gives evidence for the dependence of the method’s performance on the accuracy of the autoscaling results. Figure 7 presents some indicative examples of ionograms and ARTIST results corresponding to cases of poor (top panels) and more successful (bottom panels) performance of the method according to the results included in Tables 5–7. At this point, it should be emphasized that Jicamarca Digisonde is a DPS-4 sounder and applies ARTIST 4 for the autoscaling of the ionograms.
 |
Fig. 7. Ionograms and ARTIST results corresponding to cases of poor (top panels) and more successful (bottom panels) method’s performance. |
 |
Fig. A1. The results of the JB-2008 model splitting for September 20, 2006 at Jicamarca. Diurnal variations of the total neutral gas density and concentrations of [He], [O], and [N2] are given at 470~km in a comparison with the MSISE-00 model (solid line). Individual scattered points are smoothed (dashes) for better presentation. |
In addition to autoscaling errors, in practice there are also other sources of possible errors in the ionosonde derived electron density profiles. Especially for daytime observations obtained by Jicamarca Digisonde, McNamara et al. (2007) considered the following issues: (i) The echoes tend to become weaker at the highest frequencies that are reflected by the ionosphere, partly because the deviative absorption increases as the echoes become more and more delayed toward the highest frequency that is reflected by the ionosphere (foF2). The radiation pattern of the transmit antennas also changes with frequency, and many of the transmit antennas used for ionosondes do not have a radiation maximum in the vertical direction for frequencies above 9 MHz. The signal-to-noise ratio at these frequencies is also often affected by high interference levels. As a result, the quality of the ionogram may be significantly reduced. Indeed, the visual inspection of the ionograms used here indicates ionogram interference problems at frequencies higher than 11 MHz during solar maximum conditions. This, in conjunction with the fact that during solar minimum conditions the reflected frequencies range in principle to lower values, which are not affected, may be an explanation for the better performance of the method during such conditions. (ii) The echoes provide no direct information as to the shape, width, or depth of the ionization valley that lies between the peak of the E region and the base of the F region. This is known as the “valley problem”. Recourse is therefore made to a model of the valley, e.g., Reinisch & Huang (1983), Huang & Reinsch (1996) in case of Digisondes. The errors that arise from an incorrect model of the valley or underlying ionization decrease roughly linearly as the inverse of the frequency. They are greatest at the first frequency reflected by the F layer (fmin), and decrease to essentially zero at the peak of the F2-layer. In addition, the errors are greater for higher values of fminF/foF2, since the model is required to represent a larger part of the ionosphere. Considering that the solution of the continuity equation in our method is based on the boundary condition at 180–190 km, the valley problem may be a critical source of limitation for our method during both solar maximum and solar minimum conditions in the equatorial latitudes. Based on this discussion, one may argue that this could explain the very poor results the method gave on May 19, 2007 (see Fig. 7) and on January 09, 2002 (not shown).
5. Discussion
Our previous attempt (M2012) to retrieve thermospheric parameters from daytime middle-latitude Ne(h) profiles gave promising results. It was shown that Millstone Hill ISR Ne(h) profiles can provide neutral gas densities which coincide (within the declared accuracy) with CHAMP observations both under solar maximum and minimum conditions. Somewhat worse results were obtained with routine automatically scaled Digisonde Ne(h) profiles. The detected weaknesses were discussed there in terms with inaccuracies in the hmF2 determination and the topside Ne(h) extrapolation.
Similar attempt has been undertaken in this paper for the equatorial F2-layer. On one hand, the ISR and the Digisonde operated at Jicamarca Radio Observatory in Peru during the CHAMP and GRACE missions provided us with a very suitable database that allowed us to test our method extensively. On the other hand, a special form of the continuity equation for electron concentration was developed for the equatorial F2-region. It is of a hyperbolic type of the first order and requires only one boundary condition for its solution. In our case, this is the lower boundary condition at 180–190 km while the upper boundary at ~600 km is free. This reduces critically the input Ne(h) profile requirements, considering that for the middle-latitude version of the method, the uncertainties in the Digisonde Ne(h) topside extrapolated profile were one of the main sources of limitations in the method’s performance.
Formally the equatorial version of the method looks more consistent and simple compared to the mid-latitude one. It allows us to retrieve exospheric temperature Tex, three main neutral species [O], [O2], [N2], height independent vertical E × B plasma drift, and the total EUV solar flux with λ < 1050 Å. In principle, these aeronomic parameters are sufficient to describe the daytime Ne(h) distribution at the geomagnetic equator for heights below 500 km and solving the inverse problem makes it possible to retrieve these parameters from the observed Ne(h) profile.
Unlike Millstone Hill ISR which provides a sufficient amount of observations, Jicamarca ISR works episodically and it was possible to find only 18 cases of quasi-simultaneous ISR/CHAMP(or GRACE) observations. We speak about quasi-simultaneous observations as ISR observations may stop or start (1–4) h before or after the satellite passage in the vicinity of the Jicamarca observatory. In all cases we reduced the observed neutral gas density with the MSISE-00 model to the time of the last observed Ne(h). Regardless of such reductions, the comparison between the retrieved with the observed neutral gas densities manifests a good agreement (Fig. 5 and Table 5) with MRD = 8.7%. This is within the announced absolute uncertainty of CHAMP neutral gas density observations, which is 10–15% (Bruinsma et al. 2004) and 11% for GRACE observations (Sutton 2008). This conclusion agrees with the corresponding one found for the middle-latitude case. It is worthy to note that the agreement between the JB-2008 and the MSISE-00 estimates with the observed values for the same occasions is reflected in MRD = 32% and MRD = 27%, respectively (see Table 5 results).
The efficiency of the proposed method can be also demonstrated under special conditions (e.g., July 08 and 09, 2008) with very low observed ρ ~ 1.7 × 10−15 g cm−3 values which are much less than the predictions of MSISE-00 and JB-2008 models, which are estimated to be (2.5–3.2) × 10−15 g cm−3 (Table 5). The neutral gas densities retrieved by the proposed method are close to the observed values (1.74 and 1.91 × 10−15 g cm−3). Table 9 gives the retrieved and modeled thermospheric parameters for a quiet day Jul 08, 2008 (Ap = 2) and a moderately disturbed day Jul 12, 2008 with Ap = 16 to help in understanding why the neutral density was that low for that period. Observed, retrieved, and modeled neutral gas densities were given earlier in Table 5.
Retrieved and modeled neutral composition and temperature for quiet July 08, 2008 and moderately disturbed July 12, 2008 days. All parameters are given at 330 km.
Table 9 shows that the larger contribution to the neutral density naturally comes from the atomic oxygen. A very low retrieved neutral temperature Tn = 656 K compared to the one predicted by the empirical models (711–717) K results in low retrieved neutral gas density on Jul 08 (Table 5). On the disturbed day of July 12, 2008 the retrieved temperature is higher and the corresponding neutral gas density is larger, but both the observed and the retrieved ρ are less than models’ values (Table 5). Both MSISE-00 and JB-2008 empirical models do not include the observations during the last very deep solar minimum in 2008–2009 and naturally they cannot properly describe such special conditions. In general, the empirical models are created by fitting a set of parametric equations to an underlying database of observations. The accuracy of the models is therefore dependent on both the strength of the database as well as the ability of the parametric equations to reproduce these data for interpolation and extrapolation (Doornbos 2012). The proposed method does not bear such limitations and can give acceptable results under various geophysical conditions if reliable Ne(h) profiles are used. However for the needs of this study, empirical models are used as reference in order to assess if the method works better with ISR Ne(h) profiles or with Digisonde Ne(h) profiles.
The assessment of the method’s performance with Digisonde autoscaled Ne(h) profiles gave also acceptable results especially for solar minimum conditions – MRD ~ 12% (totally 31 cases) which is also within the announced absolute uncertainty of CHAMP neutral gas density observations (Bruinsma et al. 2004), and less than the error of the empirical JB-2008 and MSISE-00 models. However, a slightly less successful performance was evident during solar maximum conditions. In this case, the comparison between the retrieved with the observed neutral gas densities gives MRD = 16.7% and MRD = 17.5% for stationary and non-stationary scenario, respectively, which is slightly greater than the announced absolute uncertainty of CHAMP neutral gas density observations. This may attributed to ionogram interference effects in the higher frequencies reflected by ionosphere during high solar activity. The results indicate also poorer performance of the method in respect to JB-2008 (MRD = 8.3%), but a more successful one than MSISE-00 (MRD = 19.8%).
The comparison between the results obtained using as input Ne(h) from ISR and Digisondes shows a clear tendency for poorer performance in the latter case, which seems to agree with the results obtained at middle-latitudes (M2012). In the low-latitude case, this may be attributed to discrepancies between the ISR and Digisonde observed profiles due to the different measurement technique of the two instruments, to failures of the automatic scaling software implemented in Digisondes, and to limitations in the Digisonde echo detection and ionogram inversion techniques. On the other hand one may find the comparisons of Jicamarca Digisonde Ne(h) profiles with COSMIC radio-occultation observations (Chuo et al. 2011) and CHAMP in situ electron density measurements (McNamara et al. 2007) which may tell about high accuracy of the Digisonde Ne(h) profiles. All the above indicate that additional tests are required in order to extract safe conclusions on the potentiality of the proposed method in accommodating routine Digisonde profiles. These tests should include the assessment of the method with manually scaled Digisonde profiles and/or the implementation of alternative scaling techniques, as for example POLAN software (Titheridge 1988).
At the equatorial latitudes, where major phenomena of the equatorial ionosphere-thermosphere system (e.g., equatorial spread F and E) alter significantly the normal ionospheric structure, one may expect these discrepancies between ISR and Digisonde measurements to be enhanced. Nevertheless, it was shown that the proposed method allows us to extract the main thermospheric parameters from observed Ne(h) at the geomagnetic equator. In general, good or bad agreement between the retrieved and observed neutral gas density mainly seems to reflect the quality of the Ne(h) profile used for the retrieval as the method of calculations is the same. Therefore, despite the detected deficiencies, our finding seems to be encouraging by opening a way for the practical exploitation of the method for thermospheric monitoring purposes.
An important ongoing development that could drastically improve the performance of our method with autoscaled Digisonde Ne(h) profiles is the implementation of the new ARTIST 5 software (Galkin et al. 2008) to all Digisondes and the gradual replacement of the old Digisondes with new DPS 4D stations (Reinisch et al. 2008) which have much higher resolution in the scanning parameters. Such a development, in combination with a study of the effect of different topside profilers – e.g., Topside Sounder Model – assisted by Digisonde (TaD) (Belehaki et al. 2012; Kutiev et al. 2012), NeQuick 2 model (Nava et al. 2011), and the Vary-Chap model (Nsumei et al. 2012) – in the method’s performance at middle latitudes would probably enhance the potentiality of the proposed method in global scale.
6. Conclusions
The main results obtained may be summarized as follows:
-
For the first time solving an inverse problem of aeronomy in the daytime F2-region at the geomagnetic equator it was shown a principle possibility to retrieve a self-consistent set of the main thermospheric parameters (Tex, [O], [N2], [O2]) from observed electron density profiles.
-
A comparison with CHAMP and GRACE neutral gas density observations available mainly under solar minimum (2004–2010) conditions has shown that MRD of the retrieved gas densities is less than 10% corresponding to the absolute inaccuracy of CHAMP and GRACE observations providing Jicamarca Ne(h) ISR profiles are used for the retrieval.
-
Cases of very low neutral gas density observed on July 08 and 09, 2008 during the last very deep solar minimum are reproduced with our method while JB-2008 and MSISE-00 empirical models fail. This was possible as the peculiarity of these two days is reflected in the observed ISR Ne(h) profiles used for the retrieval. Overall comparison of the observed neutral gas densities with the retrieved and model values gives: the proposed method – SD = 0.39 g cm−3 and MRD = 8.7%, JB-2008 model – SD = 0.75 g cm−3 and MRD = 32%, MSISE-00 gives SD = 0.69 g cm−3 and MRD = 27%.
-
The implementation of the method with Jicamarca Digisonde Ne(h) profiles has also shown acceptable results for solar minimum conditions which are slightly worse than the results obtained with ISR N(h) profiles. This opens the way for practical applications of the method which was shown to demonstrate higher accuracy than modern empirical models provide.
Acknowledgments
The research was supported by the NATO Collaborative Linkage Grant CLG 984141 and the COST Action ES0803.
Appendix 1
The derivation of the continuity equation for electron concentration at the geomagnetic equator in 1D limited form
The continuity equation for electron concentration in the equatorial F2-region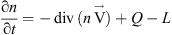 is convenient to write down in dipole coordinate system
is convenient to write down in dipole coordinate system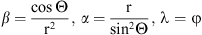 where r – geocentric distance, Θ = π/2 − Ф (Ф – geomagnetic latitude), φ – longitude, β – a coordinate along a magnetic field line, α – a coordinate perpendicular to a magnetic field line. Plasma at F2-region heights is magnetically controlled, so it can move along magnetic field lines due to diffusion and winds and perpendicular to magnetic lines due to electric fields.
where r – geocentric distance, Θ = π/2 − Ф (Ф – geomagnetic latitude), φ – longitude, β – a coordinate along a magnetic field line, α – a coordinate perpendicular to a magnetic field line. Plasma at F2-region heights is magnetically controlled, so it can move along magnetic field lines due to diffusion and winds and perpendicular to magnetic lines due to electric fields.
The dipole coordinate system is a curvilinear one, so the divergence of the flux should be written as
![$$ \mathrm{div}\vec{F}=\frac{1}{{H}_{\alpha }{H}_{\beta }{H}_{\lambda }}\left[\frac{\mathrm{\partial }}{\mathrm{\partial }\alpha }({H}_{\beta }{H}_{\lambda }{F}_{\alpha })+\frac{\mathrm{\partial }}{\mathrm{\partial }\beta }({H}_{\alpha }{H}_{\lambda }{F}_{\beta })+\frac{\mathrm{\partial }}{\mathrm{\partial \lambda }}({H}_{\alpha }{H}_{\beta }{F}_{\lambda })\right], $$](/articles/swsc/full_html/2013/01/swsc120060/swsc120060-eq9.gif) where
where
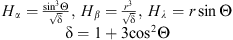
General expression for the plasma flux along the magnetic field line![$$ {F}^{//}=-{D}_{\mathrm{a}}\left[\frac{1}{{H}_{\beta }}\frac{\mathrm{\partial }n}{\mathrm{\partial }\beta }+\left(\frac{1}{{H}_{\beta }}\frac{\mathrm{\partial }\mathrm{ln}{T}_{\mathrm{p}}}{\mathrm{\partial }\beta }-\frac{1}{{H}_p^{//}}-\frac{{U}_n^{//}}{{D}_{\mathrm{a}}}\right)n\right], $$](/articles/swsc/full_html/2013/01/swsc120060/swsc120060-eq12.gif) where Da – ambipolar diffusion coefficient; Tp = Te + Ti,
where Da – ambipolar diffusion coefficient; Tp = Te + Ti,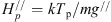 – plasma temperature and scale height,
– plasma temperature and scale height, 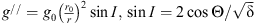 and
and 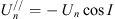 – a projection of the meridional neutral wind.
– a projection of the meridional neutral wind.
The flux divergence due to the perpendicular plasma transfer may written as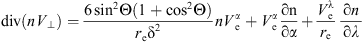 where index “e” tells that all values are taken in the equatorial plane.
where index “e” tells that all values are taken in the equatorial plane.
For practical use it is more convenient to have the continuity equation written in spherical coordinates as the thermospheric models used in calculations are given in spherical coordinates.
The following expressions are used for this transformation: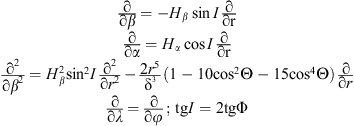
The continuity equation written in spherical coordinates looks as the following:![$$ \frac{\mathrm{\partial }n}{\mathrm{\partial }t}={D}_{\mathrm{a}}\mathrm{si}{\mathrm{n}}^2I\frac{{\mathrm{\partial }}^2n}{\mathrm{\partial }{r}^2}+\left\{{D}_{\mathrm{a}}\mathrm{si}{\mathrm{n}}^2I\enspace \left[\frac{\mathrm{\partial }\mathrm{ln}({D}_{\mathrm{a}}{T}_{\mathrm{p}})}{\mathrm{\partial }r}+\frac{1}{{H}_p}\right]-{V}_{\mathrm{nz}}-\frac{\mathrm{co}{\mathrm{s}}^4\mathrm{\Phi }}{\mathrm{\delta }}W-\frac{2{D}_{\mathrm{a}}}{r{\mathrm{\delta }}^2}\left[\enspace 1-10\mathrm{si}{\mathrm{n}}^2\mathrm{\Phi }-15\mathrm{si}{\mathrm{n}}^4\mathrm{\Phi }\right]\right\}\frac{\mathrm{\partial }n}{\mathrm{\partial }r}+\left\{{D}_{\mathrm{a}}\mathrm{si}{\mathrm{n}}^2I\enspace \left[\frac{\mathrm{\partial }\mathrm{ln}{T}_{\mathrm{p}}}{\mathrm{\partial }r}\frac{\mathrm{\partial }\mathrm{ln}{D}_{\mathrm{a}}}{\mathrm{\partial }r}+\frac{{\mathrm{\partial }}^2\mathrm{ln}{T}_{\mathrm{p}}}{\mathrm{\partial }{r}^2}\right]-\frac{2{D}_{\mathrm{a}}}{r{\mathrm{\delta }}^2}\left[\enspace 1-10\mathrm{si}{\mathrm{n}}^2\mathrm{\Phi }-15\mathrm{si}{\mathrm{n}}^4\mathrm{\Phi }\right]\enspace \left[\frac{\mathrm{\partial }\mathrm{ln}{T}_{\mathrm{p}}}{\mathrm{\partial }r}+\frac{1}{{H}_{\mathrm{p}}}\right]-\frac{\mathrm{\partial }{V}_{\mathrm{nz}}}{\mathrm{\partial }r}-\frac{{V}_{\mathrm{nz}}}{2\mathrm{\delta }r}\left(13+15\mathrm{si}{\mathrm{n}}^2\mathrm{\Phi }\right)+\mathrm{si}{\mathrm{n}}^2I\frac{\mathrm{\partial }}{\mathrm{\partial }r}\left(\frac{{D}_{\mathrm{a}}}{{H}_{\mathrm{p}}}\right)-\frac{6\mathrm{co}{\mathrm{s}}^4\mathrm{\Phi }(1+\mathrm{si}{\mathrm{n}}^2\mathrm{\Phi })}{r{\mathrm{\delta }}^2}W-R\right\}n-\frac{\mathrm{co}{\mathrm{s}}^2\mathrm{\Phi }}{r}{V}_{\phi }\frac{\mathrm{\partial }n}{\mathrm{\partial }\phi }+Q, $$](/articles/swsc/full_html/2013/01/swsc120060/swsc120060-eq18.gif) (1)where W – vertical and Vφ – zonal plasma E × B drift at the geomagnetic equator, R-linear loss coefficient γ1[N2] + γ2[O2]; Vnz = Vnx sin I cos I cos D − Vny sin I cos I sin D – vertical plasma drift due to meridional Vnx and zonal Vny thermospheric winds, D – magnetic declination.
(1)where W – vertical and Vφ – zonal plasma E × B drift at the geomagnetic equator, R-linear loss coefficient γ1[N2] + γ2[O2]; Vnz = Vnx sin I cos I cos D − Vny sin I cos I sin D – vertical plasma drift due to meridional Vnx and zonal Vny thermospheric winds, D – magnetic declination.
Directing in (1) I and Ф → 0 and neglecting zonal plasma drift we obtain the final equation for the geomagnetic equator![$$ \frac{\mathrm{\partial }n}{\mathrm{\partial }t}+\left(\frac{2{D}_{\mathrm{a}}}{r}+W\right)\frac{\mathrm{\partial }n}{\mathrm{\partial }r}+\left[\frac{2{D}_{\mathrm{a}}}{r}\left(\frac{\mathrm{\partial }\mathrm{ln}{T}_{\mathrm{p}}}{\mathrm{\partial }r}+\frac{1}{{H}_{\mathrm{p}}}\right)+\frac{6W}{r}+R\right]n=Q. $$](/articles/swsc/full_html/2013/01/swsc120060/swsc120060-eq19.gif)
Appendix 2
The JB-2008 model uses the Jacchia-71 (1971) model formalism on the barometric height distribution for the total neutral gas density. This means that individual neutral species are also controlled by the barometric law: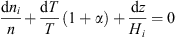 (2.1)where α – thermo-diffusion coefficient which equals 0.38 for He and 1.0 for O, O2, N2, H
i = kT/m
i
g – neutral species scale height.
(2.1)where α – thermo-diffusion coefficient which equals 0.38 for He and 1.0 for O, O2, N2, H
i = kT/m
i
g – neutral species scale height.
After the integration of (2.1) we obtain a well-known expression for the individual neutral gas concentration height distribution![$$ {n}_i(h)={n}_i\left({h}_{\mathrm{o}}\right){\left[\frac{T\left({h}_{\mathrm{o}}\right)}{T(h)}\right]}^{1+\mathrm{\alpha }}\mathrm{exp}\left(-\underset{{h}_{\mathrm{o}}}{\overset{h}{\int }}\frac{1}{{H}_{\mathrm{i}}}\mathrm{d}h\right). $$](/articles/swsc/full_html/2013/01/swsc120060/swsc120060-eq21.gif) (2.2)
(2.2)
Let us consider four heights with a 50-km step in the 300–450 km height interval. At each selected height we write down the expression for the total density. This results in a system of four linear equations with four unknown concentrations of [O], [O2], [N2], and [He] at 300 km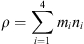 (2.3)
(2.3)
Using the JB-2008 model height dependencies for T(h) и ρ(h), in principle, the system (2.3) can be solved. In practice, however, the standard iterative methods like the Gauss-Seidel method turn out to be inefficient in this case. The solution was obtained using the methods of nonlinear programming (Himmelblau 1972).
An example of the JB-2008 model splitting is given in Figure A1 for September 20, 2006, when JB-2008 and MSISE-00 models demonstrate close neutral gas density variations at 470 km (Table 5). Each UT moment is developed individually and this results in a scatter of points, so a polynomial smoothing may be applied. A comparison of the model individual species concentrations indicates the difference up to a factor of 2.5 for [N2] and ~1.6 for [He] which take place for some hours. Partly this is due to different neutral temperature in the two models. For instance, at 1100 UT MSISE-00 gives Tex = 640 K while JB-2008 predicts Tex = 700 K.
References
- Banks, P.M., and G. Kockarts, Aeronomy, Academic Press, New York, London, 1973. [Google Scholar]
- Balsley, B.B., D.A. Carter, and R.F. Woodman, Vertical ionization drifts in the lower equatorial ionosphere and the meridional current systems, J. Geophys. Res., 81, 1296–1300, 1976. [CrossRef] [Google Scholar]
- Belehaki, A., I. Tsagouri, I. Kutiev, P. Marinov, and S. Fidanova, Upgrades to the topside sounders model assisted by Digisonde (TaD) and its validation at the topside ionosphere, J. Space Weather Space Clim., 2, A20, DOI: http://dx.doi.org/10.1051/swsc/2012020, 2012. [CrossRef] [EDP Sciences] [Google Scholar]
- Bowman, B.R., W.K. Tobiska, F.A. Marcos, C.Y. Huang, C.S. Lin, and W.J. Burke, A new empirical thermospheric density model JB2008 using new solar and geomagnetic indices, AIAA/AAS Astrodynamics Specialist Conference, 18–21 August 2008 Honolulu, Hawaii, 19, 2008. [Google Scholar]
- Bruinsma, S., D. Tamagnan, and R. Biancale, Atmospheric density derived from CHAMP/STAR accelerometer observations, Planet Space Sci., 52, 297–312, 2004. [CrossRef] [Google Scholar]
- Bruinsma, S., J. Forbes, R.S. Nerem, and X. Zhang, Thermospheric density response to the 20–21 November CHAMP and GRACE accelerometer data, J. Geophys. Res., 111, A06303, DOI: 10.1029/2005JA011284, 2006. [CrossRef] [Google Scholar]
- Chuo, Y.-J., C.-C. Lee, W.-S. Chen, and B.W. Reinisch, Comparison between bottomside ionospheric profile parameters retrieved from FORMOSAT3 measurements and ground-based observations collected at Jicamarca, J. Atmos. Sol. Terr. Phys., 73, 1665–1673, 2011. [CrossRef] [Google Scholar]
- Deminov, M.G., V.K. Kozlov, and Yu.S. Sitnov, Ionospheric O+ ions distribution over geomagnetic equator, Res. Sol. Terr. Phys., M.: IZMIRAN, 22–30, (in Russian), 1977. [Google Scholar]
- Doornbos, E., Thermospheric Density and Wind Determination from Satellite Dynamics, Springer Theses, Springer, Available from http://www.springer.com/978-3-642-25128-3, 2012. [CrossRef] [Google Scholar]
- Fejer, B.G., The equatorial ionospheric electric fields. A review, J. Atmos. Sol. Terr. Phys., 43, 377–385, 1981. [CrossRef] [Google Scholar]
- Fejer, B., and L. Scherliess, Empirical models of storm time equatorial zonal electric fields, J. Geophys. Res., 102 (A11), 24047–24056, 1997. [CrossRef] [Google Scholar]
- Fejer, B.G., J.W. Jensen, and S.-Y. Su, Quiet time equatorial F region vertical plasma drift model derived from ROCSAT-1 observations, J. Geophys. Res., 113, A05304, DOI: 10.1029/2007JA012801, 2008. [Google Scholar]
- Hedin, A.E., MSIS-86 thermospheric model, J. Geophys. Res., 92, 4649–4662, 1987. [Google Scholar]
- Himmelblau, D.M., Applied Nonlinear Programming, McGraw-Hill Book Company, New York, 1972. [Google Scholar]
- Huang, X., and B.W. Reinisch, Vertical electron density profiles from the digisonde network, Adv. Space Res., 18, 121–129, 1996. [CrossRef] [Google Scholar]
- Ivanov-Kholodny, G.S., and G.M. Nikoljsky, The Sun and the Ionosphere, Nauka, Moscow, pp. 455 (in Russian), 1969. [Google Scholar]
- Galkin, I.A., G.M. Khmyrov, A.V. Kozlov, B.W. Reinisch, X. Huang, and V.V. Paznukhov, The ARTIST 5, Radio Sounding Plasma Phys., AIP Proc., 974, 2008. [Google Scholar]
- Kudeki, E., S. Bhattachayya, and R.F. Woodman, A new approach in incoherent scatter F region ExB drift measurements at Jicamarca, J. Geophys. Res., 104 (A12), 28145–28162, 1999. [CrossRef] [Google Scholar]
- Kutiev, I., P. Marinov, S. Fidanova, A. Belehaki, and I. Tsagouri, Adjustments of the TaD electron density reconstruction model with GNSS-TEC parameters for operational application purposes, J. Space Weather Space Clim., 2, A21, DOI: http://dx.doi.org/10.1051/swsc/2012021, 2012. [CrossRef] [EDP Sciences] [Google Scholar]
- Leschinskaya, T.Yu., and A.V. Mikhailov, Description of the electron density distribution above the geomagnetic equator in the daytime F2 region of the ionosphere, Geomag. Aeron., 24, 739–744, 1984. [Google Scholar]
- Lilensten, J., Lj.R. Cander, M.T. Rietveld, P.S. Cannon, and M. Barthelemy, Comparison of EISCAT and ionosonde electron densities: application to a ground-based ionospheric segment of a space weather programme, Ann. Geophys., 23, 183–189, 2005. [CrossRef] [Google Scholar]
- McNamara, L.F., D.L. Cooke, C.E. Valladares, and B.W. Reinisch, Comparison of CHAMP and Digisonde plasma frequencies at Jicamarca, Radio Sci., 42, RS2005, DOI: 10.1029/2006RS003491, 2007. [Google Scholar]
- Mikhailov, A.V., and J. Lilensten, A revised method to extract thermospheric parameters from incoherent scatter observations, Ann. Geophys., 47 (N2/3), 985–1008, 2004. [Google Scholar]
- Mikhailov, A.V., A. Belehaki, L. Perrone, B. Zolesi, and I. Tsagouri, Retrieval of thermospheric parameters from routine ionospheric observations: assessment of method’s performance at mid-latitudes daytime hours, J. Space Weather Space Clim., 2, A03, DOI: 10.1051/swsc/2012002, 2012. [CrossRef] [EDP Sciences] [Google Scholar]
- Munninghoff, D.E., Ion and electron temperatures in the topside ionosphere, Aeron. Rep., 86, Aeronom. Lab. Univ. Illinois, Urbana, 1979. [Google Scholar]
- Nava, B., S.M. Radicella, and F. Azpilicueta, Data ingestion into NeQuick 2, Radio Sci., 46, RS0D17, DOI: 10.1029/2010RS004635, 2011. [CrossRef] [Google Scholar]
- Nsumei, P., B.W. Reinisch, X. Huang, and D. Bilitza, New vary-chap profile of the topside ionosphere electron density distribution for use with the IRI Model and the GIRO real time data, Radio Sci., 47, RS0L16, DOI: 10.1029/2012RS004989, 2012. [CrossRef] [Google Scholar]
- Nusinov, A.A., Solar activity dependence of the intensity of shortwave radiation, Geomag. Aeron. (in Russian), 24, 529–536, 1984. [Google Scholar]
- Nusinov, A.A., Models for prediction of EUV and X-ray solar radiation based on 10.7-cm radio emission, Proc. Workshop on Solar Electromagnetic Radiation for Solar Cycle 22, Boulder, Co., Ed. R.F., Donnely, NOAA, ERL, Boulder, Co, USA 354–359, 1992. [Google Scholar]
- Picone, J.M., A.E. Hedin, D.P. Drob, and A.C. Aikin, NRLMSISE-00 empirical model of the atmosphere: statistical comparison and scientific issues, J. Geophys. Res., 107, 1468, DOI: 10.1029/2002JA009430, 2002. [Google Scholar]
- Reinisch, B.W., and X. Huang, Automatic calculation of electron density profiles from digital ionograms, 3, Processing of bottomside ionograms, Radio Sci., 18, 477–492, 1983. [CrossRef] [Google Scholar]
- Reinisch, B.W., and X. Huang, Deducing topside profiles and total electron content from bottomside ionograms, Adv. Space Res., 27 (1), 23–30, 2001. [Google Scholar]
- Reinisch, B.W., I.A. Galkin, G. Khmyrov, A. Kozlov, and D.F. Kitrosser, Automated collection and dissemination of ionospheric data from the digisonde network, Adv. Radio Sci., 2, 241–247, 2004a. [Google Scholar]
- Reinisch, B.W., X.-Q. Huang, A. Belehaki, J.-K. Shi, and R. Ilma, Modeling the IRI topside profile using scale heights from ground-based ionosonde measurements, Adv. Space Res., 34, 2026–2031, 2004b. [CrossRef] [Google Scholar]
- Reinisch, B.W., X. Huang, I.A. Galkin, V. Paznukhov, and A. Kozlov, Recent advances in real-time analysis of ionograms and ionospheric drift measurements with digisondes, J. Atmos. Sol Terr. Phys., 67, 1054–1062, 2005. [CrossRef] [Google Scholar]
- Reinisch, B.W., I.A. Galkin, G.M. Khmyrov, et al., Advancing digisonde technology: the DPS-4D, Radio Sounding Plasma Phys., AIP Conf. Proc., 974, 127–143, 2008. [Google Scholar]
- Richards, P.G., Reexamination of ionospheric photochemistry, J. Geophys. Res., 116, A08307, DOI: 10.1029/2011JA016613, 2011. [Google Scholar]
- Richards, P.G., and D.G. Torr, Ratios of photoelectron to EUV ionization rates for aeronomic studies, J. Geophys. Res., 93, 4060–4066, 1988. [CrossRef] [Google Scholar]
- Richards, P.G., J.A. Fennelly, and D.G. Torr, EUVAC: a solar EUV flux model for aeronomic calculations, J. Geophys. Res., 99, 8981–8992, 1994. [Google Scholar]
- Scherliess, L., and B.G. Fejer, Radar and satellite global equatorial F region vertical drift model, J. Geophys. Res., 104 (A4), 6829–6842, 1999. [Google Scholar]
- Shim, J.S., M. Kuznetsova, L. Rastatter, D. Bilitza, M. Butala, et al., CEDAR electrodynamics thermosphere ionosphere (ETI) challenge for systematic assessment of ionosphere/hermosphere models: electron density neutral density NmF2 and hmF2 using space based observations, Space Weather, 10, S10004, s234, DOI: 10.1029/2012SW000851, 2012. [CrossRef] [Google Scholar]
- Stoneback, R.A., R.A. Heelis, A.G. Burrell, W.R. Coley, B.G. Fejer, and E. Pacheco, Observations of quiet time vertical ion drift in the equatorial ionosphere during the solar minimum period of 2009, J. Geophys. Res., 116, A12327, DOI: 10.1029/2011JA016712,2011. [CrossRef] [Google Scholar]
- Sutton, E.K., Effects of Solar Disturbances on the Thermosphere Densities and Winds from CHAMP and GRACE Satellite Accelerometer Data, A thesis submitted to the Faculty of the Graduate School of the University of Colorado for the degree of Doctor of Philosophy Department of Aerospace Engineering Sciences, 2008. [Google Scholar]
- Titheridge, J.E., The real height analysis of ionograms: a generalized formulation, Radio Sci., 23 (5), 831–849, 1988. [CrossRef] [Google Scholar]
- Torr, M.R., D.G. Torr, R.A. Ong, and H.E. Hinteregger, Ionization frequencies for major thermospheric constituents as a function of solar cycle 21, Geophys. Res. Lett., 6, 771–774, 1979. [NASA ADS] [CrossRef] [Google Scholar]
- Varney, R.H., D.L. Hysell, and J.D. Huba, Sensitivity studies of equatorial topside electron and ion temperatures, J. Geophys. Res., 116, A06321, DOI: 10.1029/2011JA016549, 2011. [CrossRef] [Google Scholar]
Cite this article as: Mikhailov A, Belehaki A, Perrone L, Zolesi B & Tsagouri I: J. Space Weather Space Clim., 2013, 3, A15.
All Tables
Selection of the solution for September 12, 2007 (~2000 UT). A non-stationary method is compared to a stationary one for several versions of calculations (see text). The minimal Δ and the corresponding neutral gas density ρ, exospheric temperature Tex, vertical plasma drift W, and ρ/Δ are given. Three maximal ρ/Δ and the corresponding ρ values are given in bold.
The contribution (%) of [He] to the total model (MSISE-00 and IB-2008) neutral gas density at the reduction heights, hred, (see text) for the cases of coincidences between observations at Jicamarca site and CHAMP (or GRACE) observations. All neutral gas densities are given in 10−15 g cm−3 units. The cases of largest [He] contribution are given in bold. LT = UT-5.
Calculated thermospheric parameters for October 29, 2008 and March 24, 2009 using non-stationary and stationary methods. The concentrations are given at 300 km, while ρ is given at 330 km for October and at 320 km for March cases for a comparison with MSISE-00 and CHAMP neutral gas densities.
Dates of available simultaneous Jicamarca ISR and CHAMP or GRACE neutral gas density observations. Observed and reduced to the heights hred neutral gas densities (10−15 g cm−3) are shown in a comparison with the calculated and model values. Calculated ρ values are corrected for the [He] contribution (see text). Daily F10.7 and Ap indices are given. LT = UT-5.
Dates of simultaneous Jicamarca Digisonde and CHAMP neutral gas density observations for the period of solar minimum. Observed and reduced to the heights hred neutral gas densities (10−15 g cm−3) are shown in comparison with the calculated and empirical models’ values. Calculated with the stationary scheme ρ values are corrected for the [He] contribution (see text). Daily F10.7 and Ap indices are given. LT = UT-5.
Dates of simultaneous Jicamarca Digisonde and CHAMP neutral gas density observations for the period of solar maximum. Observed and reduced to the heights hred neutral gas densities (10−15 g cm−3) are shown in comparison with the calculated and model values for solar maximum conditions. Both stationary (ST) and non-stationary (NST) results are presented. Daily F10.7 and Ap indices are given in the last two columns. Dashes on September 14, 2002 mean that no solution was found in that particular coincidence. LT = UT-5.
The SD and MRD statistical parameters comparing calculated and modeled neutral gas densities with CHAMP observations. Stationary and non-stationary results are also compared.
Retrieved and modeled neutral composition and temperature for quiet July 08, 2008 and moderately disturbed July 12, 2008 days. All parameters are given at 330 km.
All Figures
 |
Fig. 1. Daytime Te (solid) and Ti (dashes) profiles observed with Jicamarca ISR, where LT = UT-5. |
| In the text | |
 |
Fig. 2. Calculated Δ (see expression 4) variations to find Tex in the global minimum. Two types of Δ variations are given: with one and two minima, in any case the global minimum should be found. Calculated (dashes) with these Tex and observed (solid) Ne(h) profiles are shown. |
| In the text | |
 |
Fig. 3. Two dates with strong hmF2 variations. Arrows close to the moment of CHAMP passage over Jicamarca indicate UT moment with ISR Ne(h) observations used in the stationary scheme. |
| In the text | |
 |
Fig. 4. Fitting of the ISR observed Ne(h) profiles using a non-stationary and a stationary scheme for the periods with strong hmF2 variations (Fig. 3). Observed (solid) and calculated (dashes) Ne(h) profiles are given. |
| In the text | |
 |
Fig. 5. A comparison between the retrieved from ISR Ne(h) profiles neutral gas densities with CHAMP and GRACE observations. JB-2008 and MSISE-00 model values are also given for comparison purposes. |
| In the text | |
 |
Fig. 6. A comparison of the JB-2008 and MSISE-00 model values (top) and the calculated using Digisonde Ne(h) profiles (bottom) neutral gas densities with CHAMP observations. |
| In the text | |
 |
Fig. 7. Ionograms and ARTIST results corresponding to cases of poor (top panels) and more successful (bottom panels) method’s performance. |
| In the text | |
 |
Fig. A1. The results of the JB-2008 model splitting for September 20, 2006 at Jicamarca. Diurnal variations of the total neutral gas density and concentrations of [He], [O], and [N2] are given at 470~km in a comparison with the MSISE-00 model (solid line). Individual scattered points are smoothed (dashes) for better presentation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


