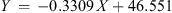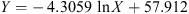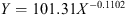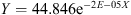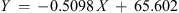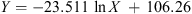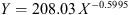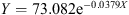| Issue |
J. Space Weather Space Clim.
Volume 3, 2013
|
|
|---|---|---|
| Article Number | A32 | |
| Number of page(s) | 17 | |
| DOI | https://doi.org/10.1051/swsc/2013055 | |
| Published online | 21 November 2013 | |
Research Article
Solar activity and transformer failures in the Greek national electric grid
Testing Research and Standards Centre, Public Power Corporation, 9 Leontariou street, GR 153 51, Kantza, Pallini, Athens, Attica, Greece
* Corresponding author: i.zois@dei.com.gr
Received:
3
August
2012
Accepted:
27
October
2013
Aims: We study both the short term and long term effects of solar activity on the large transformers (150 kV and 400 kV) of the Greek national electric grid. Methods: We use data analysis and various statistical methods and models. Results: Contrary to common belief in PPC Greece, we see that there are considerable both short term (immediate) and long term effects of solar activity onto large transformers in a mid-latitude country like Greece. Our results can be summarised as follows:
-
For the short term effects: During 1989–2010 there were 43 “stormy days” (namely days with for example Ap ≥ 100) and we had 19 failures occurring during a stormy day plus or minus 3 days and 51 failures occurring during a stormy day plus or minus 7 days. All these failures can be directly related to Geomagnetically Induced Currents (GICs). Explicit cases are briefly presented.
-
For the long term effects, again for the same period 1989–2010, we have two main results:
-
The annual number of transformer failures seems to follow the solar activity pattern. Yet the maximum number of transformer failures occurs about half a solar cycle after the maximum of solar activity.
-
There is statistical correlation between solar activity expressed using various newly defined long term solar activity indices and the annual number of transformer failures. These new long term solar activity indices were defined using both local (from the geomagnetic station in Greece) and global (planetary averages) geomagnetic data. Applying both linear and non-linear statistical regression we compute the regression equations and the corresponding coefficients of determination.
-
Key words: geomagnetically induced currents (GIC) / solar activity / technological system / non-linear phenomena / aeronomy
© I.P. Zois, Published by EDP Sciences 2013
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/2.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introductory theory – motivation
The primary cause of space weather are explosions in the Sun powered by its strong magnetic field which affect man-made technological infrastructure in space, disturb communications and GPS signals and couple through Geomagnetically Induced Currents (GICs for short) with the large-scale high voltage power grid. The most well-known case of the impact of large-scale space weather events on the electric grid is the 1989 Hydro-Quebec blackout caused by the 13 and 14 March super storm. Highly acclaimed institutions (like the US National Academy of Sciences 2008, the UK Royal Society of Engineering 2013, etc.) have issued extended reports arguing that space weather super storms may cause trillions of dollars of damage although it is acknowledged that these estimates may not be totally accurate. There is general consensus however that space weather super storms constitute a serious threat. The main cause of GICs is the interaction of the geomagnetic field with the magnetic field carried within CMEs and the surrounding background magnetised solar wind that is modulated by them.
There are several space weather phenomena which tend to be associated with a geomagnetic storm or are caused by a geomagnetic storm (see Chapman & Ferraro 1930). These include: Solar Energetic Particle (SEP) events, geomagnetically induced currents (GICs), ionospheric disturbances which cause radio and radar scintillation, disruption of navigation by magnetic compass and auroral displays at much lower latitudes than normal. In this article we shall focus on GICs and their effects on electric grids, in particular large transformers. GICs are the ground level manifestations of space weather (namely geomagnetic storms) and they are driven by the variations of the terrestrial magnetic field (temporary disturbances of the earth’s magnetosphere) via Faraday’s Law of Induction.
One can briefly describe the emergence of GICs as a six-step process (see Pulkkinen et al. 2001a, 2001b, 2003a, 2003b, 2003c):
-
Plasma is ejected from the Sun.
-
The magnetised plasma structures propagate in the interplanetary medium (solar wind).
-
Solar wind interacts with the magnetosphere. Here the dominant factor for determining how much Earth is affected is the orientation of the solar wind magnetic field. The energy feed into the magnetosphere is highest during strong reconnection of the solar wind and the terrestrial magnetic field. Increased energy flux into the system sets the conditions for dynamic changes in the magnetospheric electric current systems. One of such dynamic changes are magnetic storms which are characterised by enhanced convection of the magnetospheric plasma and enhanced ring current circulating the Earth (see, e.g., Tsurutani & Gonzalez 1997).
-
Magnetosphere-ionosphere interaction. The closure of the magnetospheric currents goes via polar regions of the ionosphere. Consequently dynamic changes in the magnetospheric currents couple to the dynamics of the ionosphere. An important class of dynamic variations are auroral substorms which are related to loading-unloading processes in the tail of the magnetosphere (e.g., Kallio et al. 2000). During auroral substorms particles injected from the tail of the magnetosphere are seen in the ionosphere in terms of auroras and rapid changes in the auroral current systems. Although some of the basic features are understood, the details of the storm and substorm processes as well as the storm/substorm relationship are one of the most fundamental open questions in the solar-terrestrial physics (see Kamide & Baumjohann 1993; Kamide 2001).
-
Rapid changes of the ionospheric and magnetospheric electric currents cause variations in the geomagnetic field which, according to Faraday’s law of induction, induce an electric field which drives an electric current in the subsurface region of the Earth. The nature of this geoelectric field depends on the characteristics of the ionospheric-magnetospheric source and on the conductivity structure of the Earth. As a rule of thumb, the magnitude of the geoelectric field increases with increasing time derivatives of the ground magnetic field and with decreasing ground conductivity.
-
Finally, the geoelectric field drives currents within conductors at and below the surface of the Earth. The magnitude and distribution of the currents are dependent on the topology and electrical characteristics of the system under investigation. The induced currents flowing in technological systems on the ground are the GICs.
From steps 3 and 4 above it is expected that the greatest GIC problems occur at high latitudes in or near the auroral zones. In these areas the geomagnetic storms are most intense and frequent since the ionospheric source is typically a localised electrojet. Countries at mid-latitude, such as Greece (latitude approximately 35° N–41° N), are located far from the magnetic pole and do not experience the same severity of geomagnetic disturbances as Canada or Scandinavia. Greece is also far from the equator and hence one does not expect severe effects due to the equatorial electrojet. GICs and their potential threat to network integrity are relatively unknown at mid-latitudes. Until recently it was believed that electricity networks in mid-latitude regions are not affected by GICs. Our research addresses this assumption, and provides insight into the incidence of GICs and the performance of the Greek electricity transmission network.
The effects of GICs on transformers are briefly the following: GICs superimpose a direct current onto the AC waveform. Yet although this direct current is usually rather small, it can shift the (B-H) curve outside the linear design operation region resulting in highly distorted output waveform, very high magnetic fluxes and half-cycle saturation (see, e.g., Bossi et al. 1983; Takasu et al. 1994; Minhas et al. 1999; Price 2002). The magnetic flux leakage from the core of the transformer may lead to overheating, gassing, shutdown and even catastrophic failure. Moreover, the distorted output wave form can create higher harmonics, can cause the triggering of the protective relays (Buchholz, etc.) and various control assets may be switched out. In addition to all the above the magnetising current can get outside the design specifications leading to increased VAr consumption and voltage instability. Let’s describe the situation with slightly more details.
GICs are driven by the variation of the (terrestrial) magnetic field, so they are characterised by slow changes. A transformer core saturates under GIC bias, causing it to operate in the extremely non-linear portion of the core steel magnetisation (B-H) curve. This quasi-direct current (GIC) flowing through a transformer offsets the power frequency magnetisation curve so that the magnetic circuit operates asymmetrically on the (B-H) curve. Transformers are designed to operate in the linear portion of the curve with only a small magnetising current, without approaching the non-linear regions of core saturation. Even small GICs can produce sufficient offset for the transformer to reach half-cycle saturation of the ac current that is in the same direction as the GICs. As the core saturates the permeability tends to 1 and the flux fills the whole space of the winding, so it is very different from the flux distribution under normal conditions. Normal leakage flux is controlled by non-magnetic (stainless steel or aluminium) shields, shunts or cheek plates, the dimensions of which are critical for controlling eddy current losses and heating. Under normal conditions, with most flux in the magnetic core, the non-magnetic plates carry little flux and generate only small losses. Under half-wave core saturation, the losses in some parts of the leakage flux shields may increase significantly, causing localised heating.
Half-wave saturation also increases the magnetising current and distorts the magnetisation current waveform (see, e.g., Takasu et al. 1994). The distorted magnetising current has harmonics that correlate well with the GIC. Without adequate control of the flux under saturation conditions, local heating in parts of the transformer may not be cooled effectively, leading to rapid temperature increase. The intensity of overheating depends on the saturation flux paths, cooling flow and the thermal condition or loading of the transformer. Overheating causes the breakdown of oil and paper insulation, leading to gassing that can be detected and analysed by dissolved gas analysis (DGA).
When a large number of transformers experience saturation due to GICs, the system’s reactive power demand increases significantly compared with the total load supplied by the transformer. Reactive power demands of this magnitude can cause severe system voltage excursions. At the same time, the change in size of the ferromagnetic material (magnetostriction) between saturated and unsaturated states at 100 times a second (at 50 Hz) causes heating, noise and mechanical vibration damage, thus possibly leading to many “mechanical” failures (e.g., broken switch axes) on top of the “electric” failures.
In the scientific literature (see, e.g., Coetzee & Gaunt 2007; Gaunt & Kohen 2009) there have been reports that GICs can cause many types of failures on transformers like: Insulation failure, tank shunting effects, local heating, rapid temperature increase causing the breakdown of the oil and paper insulation, thus leading to gassing (which can be analysed by dissolved gas analysis). The DGA records of transformers in S. Africa for example indicate that deterioration continues after the initial damage caused by GICs, affected by transformer loading and possibly other stresses (see Koen & Gaunt 2002). A transformer might fail only months after the initial damage and, unless frequent DGA samples have been taken, could appear to fail for “unknown causes” or a subsequent stress incident. Failure of transformers is often ascribed to damage of internal insulation by external overvoltages or network faults. Other significant causes of transformer failures are settling in and ageing. Copper sulphide formation in transformers or reactors with corrosive oils has recently become a concern. The coincident onset of gas generation in widely separated transformers of different ages, the relative “exposure” of the transformers to GICs, and the similarities between the nature of damage and its timing all indicate that the systemwide effect of GICs is likely to be a more significant initiator of the failures than overloading, overvoltages, system faults, copper sulphide formation or manufacturing defects. Some of these other factors may contribute to failure by weakening transformers and explain why some failed and others did not. The damage in all the transformers inspected appears to be initiated by local overheating. The DGA results are consistent with low temperature degradation of insulation. The levels of dissolved gases are below levels generally considered to be significant, and this is consistent with localised overheating.
The nature of faults caused by low temperature local overheating in windings is such that much of the evidence at the site of a fault would be obscured by subsequent disruptive failure. It is unlikely, therefore, that inspections after a disruptive fault will identify evidence of low temperature local overheating at the fault position. Unless overheating caused by leakage flux established by GICs is specifically considered, which is unlikely based on current knowledge of the problem, GICs will not be reported as a cause of faults. Does damage caused by low temperature local overheating always lead to failure and, if so, how quickly? Once core saturation by the GIC is removed, thermally damaged paper insulation will be less robust than before the event. Another mechanism of further damage must be considered, such as by leakage currents, partial discharge or reduced heat transfer through the damaged paper, causing further local heating to an extent that degradation continues. Such mechanisms could explain why gas generation and DGA levels decrease when the transformer loading is reduced. Eventually, depending on the extent of the initial damage, the presence of air and water in the transformer, and operating stresses, the damaged insulation in a small area will fail, even if the DGA levels are significantly below those usually indicating incipient failure. However, since the initial damage and the subsequent operating conditions are variable, the breakdown level or likelihood of failure is difficult to determine. In the cases reported in S. Africa and elsewhere, the DGA indicated the onset or increase of damage coincident with a severe storm. Thereafter, some transformers failed quite quickly (after a few days from the incident – this is one of the reasons for the choice of 3 and 7 days time scales after a storm for immediate failures in Section 6 – others took months, and some might survive until gradual deterioration, a severe system fault, overvoltage or another GIC event causes the damage to be extended to the point of failure. Accordingly, any transformer exhibiting an increase in levels of dissolved gases that indicate paper degradation after a geomagnetic event should be considered as distressed. The nature or location of GIC initiated damage is not the same for all the transformers. Designs differ and transformers made to the same design are not always manufactured identically. Similar GICs through similar transformers might cause slightly different patterns of leakage flux, and the weakest part of one transformer’s insulation might differ from another’s. The most likely failure point will be where leakage flux creates a condition that exceeds the local cooling capacity. In extreme cases, part of the tank or core might melt, but in most cases damage might only be observed in a winding or a lead, as in the cases reported here. The GICs should not be thought of as a single cause of a fault, but as a stress that exposes relative weaknesses, which become localised hot spots and eventually lead to failure. Thus in many cases these failures can be attributed to “ageing” or “manufacturing defects”.
GICs have cumulative and long term effects on transformers. Extreme GIC events do not occur only at the peak of or late in a solar cycle and final failure may not easily be linked to the solar cycle or a specific storm. Yet based on these responses to GICs, it would be expected that transformer failures should increase during periods following geomagnetic storms. Such a trend is evident for example from an analysis of failures of large transformers, all over 230 kV, in S. Africa and N. America. The same holds true in our case (Greece) where we observe an important increase in the number of failures 7 days after a storm.
There are some interesting implications for the analysis and reporting of failures. Excluding GICs from consideration results in all faults being ascribed to other causes. Subsequent analysis of fault data would show that GICs are not reported as a cause of faults, further obscuring the possible underlying processes of damage initiation. One of the main motivations for this research is that utility engineers (PPC or IPTO in our case here concerning Greece) should start recognising that a number of transformer failures are due to GICs, based on evidence available from storm occurrences, network analysis, incident reports and damage inspections. This in turn can attach liability to transformer suppliers with less access to the relevant data. A manufacturer that could show that failures might be associated with GICs, but that GICs were not considered or identified in specifications or incident reports by the utility engineers, could avoid or reduce any liability for damage. Avoiding damage by GICs requires that transformers be designed and built so that leakage flux resulting from saturation will not cause local overheating.
The second motivation for this work comes from mitigation: Mitigation can be implemented by suitable flux shunts, adequate clearances between the tank and core, aligning conductors so that leakage flux does not produce significant eddy currents, improving the cooling where local heating might be expected, and other techniques already used by manufacturers. Transformers have been designed, built and tested to survive saturation by high GICs. Some utilities already specify that transformers must withstand the effects of large GICs, with compliance demonstrated by finite element modelling of the flux produced. Design reviews for transformers in less exposed situations could similarly take into account the effects of GICs at levels appropriate to the network. Temporary network reconfiguration can be used to reduce the magnitudes of GICs, and might be a suitable way to reduce transformer stress in networks that are only infrequently exposed to severe geomagnetic storms, such as outside the auroral zones. Where many transformers are already installed without specified GIC capability, temporary network reconfiguration during storms may be the most effective short term mitigation procedure. Factors to be considered include the reliability of the reconfigured network, the costs of modified power despatch, the transformer risk associated with the redistributed GICs, and the conditions under which reconfiguration will be implemented. Long term mitigation can be achieved by installing series of capacitors in long transmission lines to block the quasi-DC GICs, with possible benefits for power flow capacity or even with GIC-blocking equipment.
2. Transformer failures in Greece – the collection of the relevant data
The Greek national electric grid contains 67 mega transformers (400 kV) and 501 large transformers (150 kV) plus a number of auxiliary transformers (starting from 15 kV).
The Independent Power Transmission Operator (IPTO or ADMIE in Greek) is the Greek independent power transmission operator, a fully subsidiary company of PPC (the Greek Public Power Corporation). IPTO provided data for mega and large transformer failures (namely failures for 400 kV and 150 kV transformers) throughout Greece from 1989 to 2010.
According to the IPTO (and PPC) policy a recorded transformer failure is any transformer malfunction having as a result the transformer shutdown; the duration of the shutdown can be anything ranging from 1 min up to complete destruction and total replacement of the transformer.
Again according to IPTO (and PPC) policy, recorded transformer failures are divided into two categories: These caused by human errors and all the rest. The former are recorded separately and they are used for personnel training and personnel evaluation. IPTO provided data only for the latter (with the remark that failures due to human error constitute a negligible amount). Hence we shall only consider, to begin with, recorded transformer failures caused by any reason except human error.
Going through the available data, there are some transformer failures which are obviously irrelevant to GICs. These are failures due to:
-
earthquakes,
-
falling of trees or other objects on the transformer (e.g., due to strong winds),
-
short circuits due to animals (e.g., in Greece it is relatively common to have short circuits caused by ferrets or even occasionally birds),
-
lightnings,
-
extreme weather conditions (heat or frost).
These failures have been excluded from our study. All the remaining failures are included, no matter if they are characterised as “mechanical” or “electrical” or whatever else. (For example failures due to “ageing” or “manufacturing defects” are included since there are reports on their relevance – see the previous section.) These failures in the sequel will be called simply transformer failures (TFs). We would like to mention though as an important note that these obviously irrelevant to GICs transformer failures are about 10% of the total amount of recorded failures hence even if we had included them the statistical results would not have been much different. TF were grouped on an annual basis.
Let us now explain and justify our strategy and methods. We start by exhibiting the problems and limitations: Looking at the available data for TF, it is very hard indeed to state whether a specific failure is explicitly and exclusively due to GIC (taking in mind the previous section where we explained that GICs aggravate transformers and can cause cumulative effects). In addition to this, there are no devices measuring GICs or any other sort of relevant monitoring equipment anywhere in Greece. And finally, repairing technicians – who are the people who complete the failure reports – admittedly have no training or experience whatsoever on GICs and failures related to them.
We tried to overcome these limitations with the following approach: First we divided the effects of solar activity onto transformers in two categories: Short term (or immediate) effects and long term effects (for the definition of the immediate or short term effects see the next paragraph).
For the immediate effects things were a bit complicated. Our task was to try to select possible immediate effects of solar activity on transformers by looking at TF data and reports written by technicians which are totally unfamiliar with GICs and the problems they create. Given our restrictions described above, what we did then was this: For the period 1989–2010 for which we have available data, we picked up the “stormy days”, namely days with say Ap ≥ 100 (this roughly corresponds to G2 and higher in the NOAA G-scale). For these stormy days then, we counted on how many of them we had a TF. In addition we counted how many failures we had during a stormy day or 3 days prior or 3 days after a stormy day; this is in order to take into account effects like sudden commencements of storms where rapid variations of the terrestrial magnetic field occur. We did the same for a 7 day period (before or after a stormy day). The rationale behind this is that TFs occurring during a stormy day (or “around” a stormy day) are very much possible to be caused by GICs indeed. Thus we give the relevant frequency (frequency of occurrence of failures during a stormy day) along with explicit examples which we briefly present and analyse. This provides an answer to the question of the assessment of the immediate or short term effects of solar activity onto transformers.
The later, namely long term effects of solar activity onto transformer failures are – in principle at least – perhaps simpler to deal with and quantify: We use various analytic and statistical methods, in particular linear and non-linear statistical regression and correlation. As an independent variable we use some newly defined long term solar activity index and as a dependent variable we use the annual number of transformer failures. One basic problem we had to overcome here at the very start was to create a suitable long term solar activity index since there was no one readily available.
3. Solar activity (long term indices) data
In order to assess-study the long term effects of solar activity on transformers, the idea is to try to statistically correlate transformer failures with solar activity. The subtlety here is that we need some “indices” with the same time scale for these two groups of data. From the transformer failures’ side, things are pretty straightforward, the annual number of transformer failures throughout Greece is probably the most reasonable index (counting the number of transformer failures on a monthly basis may have some logic yet it is not very convenient; any shorter time scale than that, weekly, daily or hourly basis, is clearly senseless). On the solar activity side things are not so straightforward. A very reasonable index measuring solar activity is the number of sunspots, given on an annual basis. The number of sunspots follows well (in fact partly defines) the 11-year solar activity cycle (bell-shaped graph). The problem with this index (annual number of sunspots) though is that it is “indirect” for our purposes. We are primarily interested in earth affecting solar activity (and not just solar activity in general) and for this purpose the number of sunspots is relevant but not directly relevant; for example in sunspot regions flares or CMEs tend to be created but whether they affect the earth and up to what extend, depends on the size of flare or CME, the relative position (direction and magnitude) of the flare with the current position of the earth (sun-earth line). Thus a more direct index should be directly related to the variations of the magnetic field of the earth caused by the ejected plasma from the sun. After all the creation of GICs (which is what affects transformers) is due to the Faraday Law in classical electromagnetism which relates electric fields and currents with variations of the magnetic field. Now there are indeed certain indices measuring these variations of the terrestrial magnetic field, the most important and well-known ones are the Ap index (and its logarithmic version the Kp index along with some variations) and the Dst index (see Broun 1861; Adams 1892; Chapman 1935; Bartels et al. 1939; Chapman 1952; Kertz 1958, 1964; Akasofu & Chapman 1964; Cahill 1966; Sugiura & Hendricks 1967; Frank 1970; Akasofu & Chapman 1972; Fukushima & Kamide 1973; Crooker & Siscoe 1981; Rangarajan 1989; Sugiura 1991; Tascione 1994; Campbell 2002; Carlowicz & Lopez 2002). The problem with these indices however is that they are short term indices, they are daily planetary averages from about a dozen stations on the globe. We need a long term (on an annual basis) index of the earth affecting solar activity. So the picture is this: On the one hand the annual number of sunspots is a good long term index of solar activity but it is characterised as indirect for our purpose, whereas on the other hand the Ap and Dst indices are direct but short term indices (see Moos 1910; Vestine et al. 1947; Hess 1968; Haymes 1971; Rostoker 1972; Shelley 1979; Langel et al. 1980, 1981; Mayaud 1980; Smith et al. 1981; Williams 1980, 1981; Van Allen James 1983; Lehtinen & Pirjola 1985; Hamilton et al. 1988; Parks 1991; Walt 1994; Kivelson & Russell 1995). It is not easy to get a direct index out of the number of sunspots but there are a number of possibilities to define some long term (on an annual basis) solar activity indices using the Ap and Dst data: One can count the number of “disturbed” days per year, namely annual number of days with say Ap ≥ 40 and Dst ≤ −40. The value 40 was chosen from the NOAA Boulder Colorado station scale table and the NOAA Space Weather Scale for Geomagnetic Storms (NOAA G-scale): it seems a reasonable choice since the A-index is the daily average of the equivalent a indices and a value of a = 40 corresponds to roughly a situation between G0 and G1 (G0 means no practical effects, G1 means minor practical effects on man-made systems on earth). Table 1 indicates the correspondence between the K-index, the a-index, the variations of the terrestrial magnetic field ΔB and the NOAA G-scale.
Boulder Colorado station scale table
This long term index has the disadvantage that we count the disturbed days but not the severity of the solar storms. Another option would be to count the annual sum of the Ap and Dst indices, in this case we take into account both the number of storms and their intensity. A third option is to consider the annual average of the Ap and Dst indices. The difference between the annual sum and the annual average is the division by 365 (or 366) and for linear models this makes no difference (as one can easily check by looking at the relevant formulae) but it does make some (little as we shall see in one example) difference in non-linear models. Our final option was to consider the annual mean of the daily sum of the 3 h K-index of the local Penteli Magnetic Observatory near Athens. This last option makes use of local geomagnetic data (and not planetary averages like the Ap and Dst).
If we restrict our study to linear regression and correlation (thus ignoring non-linear phenomena, which is not too bad as a first approximation), it follows easily from the relevant formulae (mathematical statistics) that instead of studying for example the linear correlation between two variables say X and Y, one can equivalently study their scalar multiples aX and bY (where a, b real scalars), the results remain the same (the correlation coefficient does not change). In this case if we simply divide the annual sum of Ap and Dst by the annual number of days (365), we get the annual average of Ap and Dst. Hence for linear regression and correlation, the annual sum of Ap (and Dst) can be replaced by the annual average of these indices.
In Table 2 we give the solar activity long term indices data: SSN stands for (Annual) Sunspot Number; SSN data were provided by NASA
Long term solar activity data
http://solarscience.msfc.nasa.gov/greenwch/spot_num.txt
All the rest of the data were provided by the UK Solar System Data Centre UKSSDC. Dst data are only available until 2008. For 2009 and 2010 we used provisional data.
We give the relevant graph: Figure 1 gives the graphs of all these long term indices (which are scaled in order to match the SSN values). We observe that all these indices have the general shape of the SSN curve, they exhibit roughly the same periodicity as SSN (11-year solar cycle).
 |
Figure 1. Long term solar activity indices (all scaled except SSN) vs. Time graph. |
4. Long term effects
4.1. Global indices
For the long term effects we shall use various statistical methods and tests. The simplest thing to do in order to start our study would be to run a linear regression model (see Zois 2011) between transformer failure number (TFN) and sunspot number (SSN). The sunspot number (SSN) will be our independent variable X, whereas the transformer failure number (TFN) will be our dependent variable Y. The (linear) regression equation we find is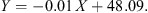
The slope is −0.01, the y-intercept equals 48.09, the corresponding correlation coefficient is r = −0.52 and the coefficient of determination equals r 2 = 0.27. These parameters were estimated using the ordinary least squares method (with the use of R and Microsoft Excel). We give in Figure 2 the relevant scatter plot along with the linear regression line.
 |
Figure 2. SSN vs. TFN scatter plot. |
One interesting feature here is that the slope is negative (negative correlation). This means that when SSN increases, TFN decreases. At first sight this might seem odd but there is a good explanation and in order to reveal it, one has to go a bit deeper (Zois 2011): In Figure 3 we plot the SSN (blue) and TFN curves (red and green) vs. time in a single graph and we observe that (although the TFN has considerable noise and fluctuates), there is a “phase delay” between the two curves which is roughly equal to 4 and 5 years, namely approximately slightly less than half a solar cycle. For a clearer visual exhibition of this phase delay we have also plotted the smoothed (and scaled) TFN curve (green). This means that the maximum number of failures occurs towards the end of the solar cycle when solar activity attains its minimum. This is due to the cumulative nature of solar activity effects on transformers in the long term: There is a building up phenomenon, as time passes solar activity aggravates transformers and failures occur after some “threshold” (related to the durability of key transformer components) is crossed. In Greece, which is a mid-latitude country, GICs are not so high and this threshold is crossed later in a solar cycle (towards the end). (In Figure 3 we have scaled the TFN curve for clearer visual exhibition). So Figure 3 verifies the negative sign of the correlation coefficient of the linear approximation.
 |
Figure 3. (Scaled) TFN and SSN vs. Time graph. The blue curve is SSN, the red curve is the (scaled) TFN and the green curve is the smoothed (and scaled) TFN. |
We can perform a hypothesis testing (Daniel & Terrell 1995) using statistical inference to see if there is (linear) correlation between our variables X (SSN) and Y (TFN). We want to test the null hypothesis H
0: ρ = 0 (no correlation, ρ denotes the population correlation coefficient, r, which denotes the sample correlation coefficient, is an estimator of ρ) against the alternative hypothesis H1: ρ ≠ 0 (there is correlation). We choose the a = 0.05 confidence level and we use Student’s t-variable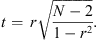
This is a one-sided test, hence we look at t 0.975 with N – 2 = 22 – 2 = 20 degrees of freedom. The critical value then of t is 2.086. Since by the above formula we compute t = −2.724 (namely in absolute value larger than the critical value), we reject the null hypothesis. Thus there is correlation.
The next order of business is to try some non-linear models (with respect to the variable X). The basic ansatz here is that there is a continuous function Y = Y(X) relating the independent variable X (which is some long term solar activity index) with the dependent variable Y, which is the annual number of transformer failures. We have studied the following functional models: logarithmic, polynomial (degrees 1–6), hyperbolic and exponential (Pedhazur 1982; Barlow 1993; Goodall 1993; Nievergelt 1994; Björck 1996; Draper & Smith 1998; Pindyck & Rubinfeld 1998; Cohen et al. 2003; Kaw & Kalu 2008; Venables & Smith 2013):
Logarithmic:
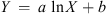 where a, b are real parameters.
where a, b are real parameters.
Polynomial of degree 2 up to 6 in X: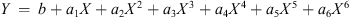 where a
1, a
2, a
3, a
4, a
5, a
6 and b are real parameters.
where a
1, a
2, a
3, a
4, a
5, a
6 and b are real parameters.
Hyperbolic:
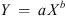 where a, b are real parameters.
where a, b are real parameters.
Exponential:
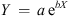 where a, b are real parameters.
where a, b are real parameters.
We estimate the parameters using again ordinary least squares. We apply all these functional models to all our long term indices (see Zois 2012, 2013a, 2013b). The results are summarised in Table 3 which contains the equations and the corresponding coefficients of determination R 2.
Summary of regression results (global geomagnetic data).
In the non-linear case, when one uses a scalar multiple of the variable this can make some difference, hence it makes sense to try to use the annual sum of the Ap or Dst index instead of the annual mean. However as we shall see in our case the difference is small, practically non-existing. As an example we consider the annual Dst sum (absolute value, instead of the annual Dst mean):
Annual Dst sum (absolute value) vs. TFN
Polynomial: Among polynomials in X with degrees from 2 up to 6, the largest coefficient of determination was given using a polynomial of degree 6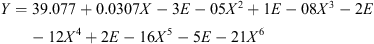 with R
2 = 0.22.
with R
2 = 0.22.
If one compares the coefficient of determination results between annual Dst sum and annual Dst mean the differences are practically non-existing.
We use the coefficient of determination as an indicator for the goodness of fit of the curve to the data. Clearly the largest coefficient of determination R 2 = 0.35 was obtained using SSN as the independent variable and a polynomial of degree 6 as formula. From the more direct indices the largest coefficient of determination was obtained using the annual Dst mean with R 2 = 0.23 and again a polynomial of degree 6. Very close lies the coefficient of determination using the Annual number of days with Dst ≤ −40, R 2 = 0.22. It is perhaps surprising to see better fitting when we use the SSN which is not a direct index. The explanation for this is mathematical convenience: This is a physics vs. maths game, physics prefers Dst as being a more direct index for our purpose yet maths (statistics) prefer SSN which has a smoother graph as a function of time (we discuss this issue in greater detail in the last section “Conclusions”).
4.2. Local indices
The long term solar activity indices used in the previous subsection were defined using planetary averages like the Ap and Dst indices data. In this subsection we use some local geomagnetic data from the Geomagnetic Observatory of Penteli (GOP for short, its I.M.O. code is PEG) which is located about 30 km North East of Athens
http://www.magstation.gr/geomagnetism/wiki/Main
GOP belongs to IGME, the (Greek) Institute of Geology and Mineral Exploration
http://www.igme.gr/portal/page?_pageid=33,56803&_dad=portal&_schema=PORTAL
This is the only geomagnetic station existing in Greece. It became a member of IMO (Intermagnet group/network) on the 8th of November 2010
http://www.magstation.gr/geomagnetism/wiki/News
For the period we are interested in, namely 1989–2010, GOP could only provide the 3 h K-index data. Using the data provided by GOP, as a long term (direct, local) solar activity index we defined the annual mean of the daily sum of the 8 3 h K-indices measured by GOP.
For instance Penteli gave us the 3 h K-index for all days from 1989 to 2010.
Thus we computed the annual mean of the daily K-index sum and this is what we used as a long term (local) solar activity index.
Table 4 gives the annual mean of the daily K-index sums from GOP.
Annual Average of the daily K-index sum (GOP).
In Figure 4 we give the graphs of SSN and (scaled) Annual mean of daily K-index sum from Penteli vs. Time. One can see that it follows the general pattern of SSN, periodicity, two picks and two valleys.
 |
Figure 4. SSN (blue) and scaled (multiplied by a factor of 95) Annual mean of the daily K-index sum from Penteli (purple) vs. Time graph. |
Next we run the same regression models as we did in the previous subsection (both linear and non-linear) and we write down our results:
Polynomial: Among polynomials in X with degrees from 2 up to 6, the largest coefficient of determination was given using a polynomial of degree 6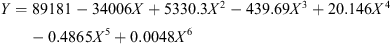 with R
2 = 0.23.
with R
2 = 0.23.
It is clear that the best fitting curve is the polynomial of degree 6 with a coefficient of determination equal to R 2 = 0.23. We summarise our regression results using Penteli data in Table 5.
Summary of Regression results (local geomagnetic data from Penteli).
Now in order to be as mathematically rigorous as possible, for this “best fitting curve” (polynomial of degree 6), we have to check some assumptions regarding non-linear regression and the ordinary least squares method used to estimate the relevant parameters. The basic assumptions we have to check are homoscedasticity and normality of the residuals (we assume weak exogeneity and there is no question about multicollinearity since essentially we use only one independent variable). If these tests fail that would mean that the ordinary least squares method used to estimate the parameters of the order six polynomial curve should be replaced by a more elaborate method (like weighted least squares or perhaps generalised least squares or iteratively weighted least squares).
The residuals are given in Table 6.
Residuals of polynomial of order six curve (annual average of daily K-index sum vs. TFN).
In order to check normality we perform the Shapiro-Wilk test (Shapiro & Wilk 1965) for the residuals. Essentially we test the null hypothesis that the residuals are normally distributed against the alternative that they are not. At the a = 0.05 confidence level, in our case the W statistic equals 0.93 and since the threshold equals 0.91, we cannot reject the null hypothesis, hence the null hypothesis is accepted and thus the residuals come from a normal population.
In order to check homoscedasticity we perform the Bartlett test of homogeneity of variances (see Snedecor & Cochran 1989) for the residuals. We divide the residuals in two groups, the first group consists of the first 11 and the second group consists of the remaining 11 residuals (22 in total). We compute the variances of the two samples, the first one equals 103.4, the second one equals 108.3. The Bartlett test is essentially the test of the null hypothesis that the variances of the two samples are equal against the alternative that they are not. The relevant test statistic, Bartlett’s K square follows the chi square distribution. In our case we have two samples hence one degree of freedom. At the a = 0.05 confidence level the critical value is 0.946. The Bartlett’s K square we compute is 0,00861. Since this is not larger than the critical value we cannot reject the null hypothesis that the variances are equal, thus we accept the null hypothesis that the variances are equal and hence the residuals (errors) are homoscedastic.
5. Extreme regression
In this section, in order to increase the coefficient of determination we perform two tasks:
-
Try to push polynomial regression to the limit, namely increase the polynomial degree up to the maximum value for which the least squares method can be successfully applied (i.e., the coefficients can be determined – namely one does not have an overconstrained or overdetermined system, that the coefficients are unique and without singularities, Runge’s phenomenon appearing, etc.).
-
Based on the Stone-Weierstrass theorem from functional analysis (Rudin 1976; Jeffreys 1988), we try to use another, more elaborate unital subalgebra of C([a,b],R) (algebra of real continuous functions defined on an interval [a,b]) which separates points in [a,b], like the algebra of orthogonal polynomials instead of the algebra of ordinary (raw) polynomials (see, e.g., Glicksberg 1962; Zois 2009, 2010, 2013a, 2013b). We used R language and our results are summarised in Table 7 (as references for the orthogonal polynomials used in R see Kennedy & Gentle 1980; Chambers & Hastie 1992).
Table 7.Higher degree polynomial regression results.
The annual number of days with Dst ≤ −40 long term index gives a rather impressive R 2 value of 0.88 using orthogonal polynomials (of 15th degree).
6. Short term (immediate) effects
For an assessment of the short term effects of solar activity onto large transformers we follow what we described in Section 2 above. First, in Table 8 we present some key points from our study of the transformer failure data: in one column we have put the max Ap value with its specific date for each year. The next column counts the number of stormy days (Ap ≥ 100 or Dst ≤ −100) during each year. And then we count the failure stormy days in the next column, namely the stormy days on which some failure occurred (plus failures on max index day or 2–3 days after max index day but these are very few cases). Similarly for the Dst index.
Overall Short term effects.
A possible simple “cumulative short term effect index” would be the average (over the 22 years) of the fraction.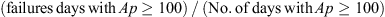 and similarly for the Dst index.
and similarly for the Dst index.
Alternatively we could take the sum of failure days with Ap ≥ 100 from 1989 to 2010 and divide it with the total sum of days with Ap ≥ 100 again from 1989 to 2010 (and similarly for the Dst index). This will give for Ap the fraction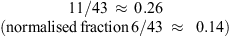 and similarly for the Dst one computes
and similarly for the Dst one computes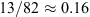
In order to be able to interpret the above numbers as the (empirical) probability (or experimental probability or relative frequency) to have a failure during a stormy day the quotients have to be normalised. A simple way to do that would be to consider only one failure for each stormy day (there may be more than one, e.g., see 7 April, 1995 in the Failure days with Ap ≥ 100 column in Table 8) and to consider strictly failures occurring during stormy days alone (and not failures during “around” stormy days). This shows that Ap is perhaps a “more indicative” index for immediate-short term effects in Greece which motivated us to give also in Table 9 another assessment of the immediate-short term effects: We include two extra columns, the ±3 days column which counts the number of failures occurring during the stormy days, namely the day with Ap ≥ 100, plus the number of failures occurring 3 days before or 3 days after the stormy days; similarly for the ±7 days column.
Ap cumulative short term table.
Similar simple indices can be calculated and they can be interpreted (after proper normalisation) as the experimental (a posteriori) probability to have a failure during a stormy day plus or minus 3 days (and similarly for the 7 days case).
Next we describe briefly some specific examples along with some comments. We focus on cases with Ap ≥ 100 or Dst ≤ −100 or both.
1989
One Case study for an immediate effect: On 21 October, 1989 the planetary Ap mean was 146 and the Dst planetary mean was −191. In an 150 kV transformer in Alouminion, Central Greece, the Buchholz relay of the tap changer was triggered. The cause was recorded as “unknown”. This incident is a very possible immediate effect of solar activity (in particular GICs) on a transformer.
In 1989 there were 5 days with Ap ≥ 100: 13.3, 14.3, 20.10, 21.10, and 17.11. During the March storm no failures were reported a week before or after the storm. During the October storm there was one reported failure on the 21st October and four failures the week before (no failures the week after). During the November storm there was one failure 3 days before and one failure 3 days after the storm (and two failures one week after the storm).
In 1989 there was the Quebec black-out in Canada due to the solar super storm on 13–14 March 1989. There were no (immediate) recorded failures in the Greek power grid caused by this solar storm.
1990
One Case study for an immediate effect: On 30 March 1990 where the planetary Ap mean was 69 and the Dst planetary mean was −106. In an 150 kV transformer in Alexandroupolis (NE Greece) there was a tap changer malfunction; the tap changer was replaced.
In 1990 there were 2 days with Ap ≥ 100: 10.4 and 28.7. No reported failures 1 week before or after these storms. However on 12, 13, 14 June the Ap was between 70 and 90 and there was one reported failure on the 15th June.
1991
Three Case studies for immediate effects:
-
On 24 March 1991 where the planetary Ap mean was 161 and the Dst planetary mean was −75. In an 150 kV transformer in Oinofita (N of Athens) there was a tap changer malfunction which was repaired.
-
On 5 June 1991 where the planetary Ap mean was 196 and the Dst planetary mean was −147. In an 150 kV transformer in Thiva (N of Athens) there was a tap changer malfunction which was repaired. The report said “malfunction caused (in all likelihood) by overheating of unknown cause”.
-
On 29 October 1991 where the planetary Ap mean was 128 and the Dst planetary mean was −173. In an 150 kV transformer in Alexandroupolis (NE Greece) the differential protection relay was triggered; also some oil leakage was observed. The tap changer was replaced, insulator replaced.
1991 was a very active year, there were 11 days in total with Ap ≥ 100: 24, 25, 26 March and there was a reported failure on the 24th and one on the 20th. In June on 5th, 10th and 13th Ap was larger than or equal to 100 and we had one reported failure on the 5th and four more in between a week of the stormy days. In July the Ap was larger than or equal to 100 on the 9th and 13th and we had two failures on the 7th and on the 6th (3 days before the 9th). Finally Ap was larger than or equal to 100 on 29 October, 1 November and 9 November. We had a reported failure on 29 October, one reported failure on the 25 October, one on 8 November and one on 14 November.
1992
One case study for an immediate effect: On 27 February 1992 where the planetary Ap mean was 60 and the Dst planetary mean was −101. In an 150 kV transformer in Ptolemaida (N Greece) the differential protection and Buchholz relays were triggered and the failure was repaired.
In 1992 there was only 1 day with Ap ≥ 100 (10.5) and there was one reported failure one week after the storm (17.5).
1993
One case study for an immediate effect: On 13 September 1993 where the planetary Ap mean was 91 and the Dst planetary mean was −109. In an 150 kV transformer in Lamia (Central Greece) there was a tap changer malfunction which was repaired.
In 1993 there were no days with Ap ≥ 100.
1994
Zero case study for an immediate effect.
In 1994 there was only 1 day with Ap ≥ 100 (17.4). There was one reported failure 3 days after (and another one 8 days after). Moreover on 03.04 Ap was 92 and there was one reported failure the day before and another one 3 days after.
1995
Two case studies for an immediate effect: On 7 Apri 1995 where the planetary Ap mean was 100 and the Dst planetary mean was −82. In two 150 kV transformers, one in Corfu (NW corner of Greece) and another in Iasmos (N Greece) there were reported failures: In the first case there was inability to switch from 15 kV to 21 kV and in the second the Buchholz relay was triggered. In both cases the failures were repaired.
In 1995 there was 1 day with Ap ≥ 100 (7 April). There were two reported failures on that day, one failure the day before (6 April) and another one 6 days before (1 April)
1996
Zero case study for an immediate effect.
In 1996 there was no day with Ap ≥ 100.
1997
One possible case study for an immediate effect: On 23 November 1997 where the planetary Ap mean was 59 and the Dst planetary mean was −88. In one 150 kV transformer in Sindos Thessaloniki (N Greece) the Buchholz and differential protection relays were triggered. The whole transformer was replaced.
In 1997 there was no day with Ap ≥ 100.
1998
Zero case study for an immediate effect.
In 1998 there were 3 days with Ap ≥ 100: 04.05 (with one failure 4 days before), 27 August (with no failures one week before or after this date) and 25 September with one failure 6 days after.
1999
Zero case study for an immediate effect.
In 1999 there were no days with Ap ≥ 100.
2000
One possible case study for an immediate effect: On 18 September 2000 where the planetary Ap mean was 70 and the Dst planetary mean was −104. In one 150 kV transformer in Komotini (N Greece) there was oil leakage due to an unknown reason. The failure was repaired.
In 2000 there were 3 days with Ap ≥ 100: On 15 July (with one failure 7 days after), 12 August (with one failure 6 days before and another failure 4 days after) and on 5 October (with two failures 6 days after).
2001
One possible case study for an immediate effect: On 1 April 2001 where the planetary Ap mean was 38 and the Dst planetary mean was −137. In one 150 kV transformer in Polihni Thessaloniki (N Greece) there was a failure characterised as “mechanical”, broken switch transmission axis. The recorded cause for the failure was “ageing”. The failure was repaired.
In 2001 there were 3 days with Ap ≥ 100: On 31 March (with one failure 4 days before and one failure the next day), on 6 November (with one failure 7 days after) and on 24 November (with two failures 5 and 6 days before).
2002
Zero possible case study for an immediate effect.
In 2002 there were no days with Ap ≥ 100.
2003
Zero possible case study for an immediate effect. There were two notable solar storms on 30th October 2003 and 20th November 2003. No recorded transformer failures around these days in Greece (in fact there were no recorded failures from 26 October until 3 December).
In 2003 there were 6 days with Ap ≥ 100: On 29 May (no failures in between 7 days, yet six failures in the next month), on 18 August (with one failure 6 days before), on 29, 30, 31 October (with one failure on 26 October) and on 20 November (no failures in between one week).
2004
Zero possible Case study for an immediate effect. However, there was a solar storm on 27 July with annual Ap max and 2 days later on 29 July there was a failure on a 150 kV transformer in Sfikia (N. Greece). There was a failure in the cooling system which was repaired. The recorded cause of this failure was “manufacture defect”. Also on 31 July and on 4 August there were also recorded failures on 150 kV transformers in W. Greece (Florina and Kanalaki, respectively). In the first case (Florina, 31 July), the Buchholz and differential protection relays were triggered. The recorded cause of the failure was “manufacture defect”. In the second case (Kanalaki, 4 August) the differential protection relay was triggered, no cause recorded. Moreover on 8, 9 and 10 November the Dst values were −210, −125 and −176 respectively. Five days later, on 15 November there was a failure on an 150 kV transformer in N. Greece (Arachthos). No further details given in the failure report form.
In 2004 there were 5 days with Ap ≥ 100: On 25 and 27 July (with three failures 7 days after) and on 8, 9, 10 November (with one failure 5 days after).
2005
One possible case study for an immediate effect: On 11 September 2005 where the planetary Ap mean was 101 and the Dst planetary mean was −84. In one 150 kV transformer in Salamis (Central Greece, of the West coast of Athens) there was a failure in a casing gasket which was replaced. The failure was due to “manufacture defect” according to the failure report.
In 2005 there were 2 days with Ap ≥ 100: On 24 August (with one failure 2 days after and another one 8 days after) and on 11 September (with 1 failure 7 days before and another one 4 days after).
2006
One possible case study for an immediate effect: On 14 April 2006 where the planetary Ap mean was 65 and the Dst planetary mean was −63. In one 150 kV transformer in Lavrio (Central Greece, near Athens) there was a recorded failure with no explanation or possible cause. There was however the note that that particular transformer was functioning since 1971 with no failures, hence it was implied that the cause was ageing.
In 2006 there were no days with Ap ≥ 100.
2007, 2008, 2009, 2010
Zero possible case study for an immediate effect.
During those years there were no days with Ap ≥ 100.
7. Conclusions
In this work we tried to provide evidence that solar activity affects large transformers (400 kV and 150 kV) in Greece. Effects are divided into short term (immediate) and long term effects. The common belief in PPC for many years (in fact since its founding in 1950s) was that there are no such effects because Greece is a mid-latitude country (latitude approximately 35°–41° North). The second goal was to provide a method to assess solar activity long term effects on large transformers by using various analytic and statistical methods.
Let us start with the short term (immediate) effects: We used transformer failures data for the period 1989–2010 provided by IPTO (ADMIE), the Greek independent power transmission operator, a fully subsidiary company of PPC (the Public Power Corporation of Greece). After some data clearance (in order to get rid of obviously irrelevant to GICs failures), we ended up with a list of transformer failures which could be related to GICs. This task had some difficulties since PPC personnel are not trained on GICs (like say their co-workers in other countries where for example technicians have to fill in specific repairing forms in the shape of a questionnaire, thus helping to identify GIC-related failures easier). Nonetheless, having our set of transformer failure data at hand, we juxtaposed it with solar activity data and we saw classic cases of GIC-related failures like triggering of protecting relays, oil leakage due to insulation destruction, etc., appearing on days of elevated solar activity (say Ap index larger than 100). We obtained clearance to publicise some of these cases and briefly analysed them in Section 6 (see also Table 8).
However, there are also rapid variations of the terrestrial magnetic field a few days prior to a solar storm (see Dessler et al. 1960; Tsunomura 1998) and for this reason we extended our research not only on stormy days but also on short periods around a stormy day: We chose two additional time scales, ±3 days and ±7 days around a stormy day. The plus or minus 3 days time scale was chosen in order to include effects due to sudden commencement of a storm – primarily for the “minus” part. We also observed that there is an important increase in failures during days +4, +5, +6 and +7 from a stormy day and thus we decided to include the ±7 days time scale as well (the minus was included for “symmetry”, there were no observed failures during −4, −5, −6 and −7). Taking a closer look of the data we saw evidence that this second scale captures failures triggered shortly after a storm and reveals “weaknesses” of the transformers like bad maintenance, etc. Hence during the period of interest (1989–2010), there were 43 stormy days (namely days with Ap ≥ 100) and we observed 19 failures occurring during a stormy day plus or minus 3 days and 51 failures occurring during a stormy day plus or minus 7 days (see Table 9).
As an attempt to assess in a cumulative manner the probability to have a transformer failure somewhere in Greece during a day of high solar activity we simply counted the number of stormy days (namely days with Ap ≥ 100 or Dst ≤ −100) and then we counted in how many of them we observed a transformer failure and by division we got an idea of a probability (or relative frequency) to have a transformer failure during a stormy day (or around a stormy day).
For the long term effects: We had to define some new long term solar activity indices and then we tried to quantify the long term effects using statistical and analytic techniques. Long term solar activity indices have been defined using both global (namely planetary average) short term indices data (like Ap and Dst data) and local (from the Penteli Magnetic Observatory near Athens) short term indices data (like the 3 h K-index data). In particular we defined and used six long term indices, five using global data and one using local data: The former include the annual number of sunspots (SSN), the annual Ap mean, the annual Dst mean (and the annual Dst sum), the annual number of disturbed days, namely days with Ap ≥ 40 and the annual number of days with Dst ≤ −40. The only local geomagnetic data available for the period of interest (1989–2010) was the 3 h K-index provided by the Geomagnetic Observatory of Penteli near Athens. Using these K-index data we defined the annual mean of the daily K-index sum which we used as a long term local solar activity index.
The first important fact revealed from our analysis, concerning the long term effects of solar activity onto large transformers, is shown in Figure 3 where we plotted both SSN (annual sunspot number) and TFN (annual transformer failure number) as functions of time in the same graph: In Figure 3 we observe two striking (at least for PPC technicians) facts:
-
A part from noise, failures do show periodicity similar to the periodicity of solar activity (the solar cycles).
-
The two graphs seem to have a “phase delay” roughly half a solar cycle (more precisely 4–5 years).
Let us make some comments on these facts: This rather revealing graph indicates that the annual number of failures generally follows the solar activity pattern, it has a periodicity similar to the 11-year solar cycle but it has a “phase delay”: During solar cycle 22 (1986–1996) the max number of sunspots was observed in 1989 and the max number of failures was observed in 1993 (4 years later). During solar cycle 23 (1996–2008) the max number of sunspots was observed in 2000 and the max number of failures was observed in 2006 (6 years later). So by average the phase delay is about 5 years later, roughly half a solar cycle. This can be explained by the fact that GICs in Greece are existing but smaller compared to say Scandinavian countries and cumulative effects dominate; there is a building up phenomenon related say to erosion of transformer components, say insulators: Failures occur after some threshold is crossed and since GICs in Greece (latitude approximately 35°–41° N) are generally smaller, this threshold is crossed later (the erosion of components is not so fast). Similar, relatively “mild” effects were reported from the US power grid (see Schrijver & Mitchell 2013) where the focus was not on component – transformer failures but on the grid’s inability to maintain power quality, thus including outages as well as voltage sags and frequency shifts. So the picture is that as latitude increases, this phase delay should decrease, namely in say Scandinavian countries one would expect very little or no phase delay at all (well, one has to be more careful here since failures also depend on ground conductivity, grid topology, etc., the above conjecture assumes that all other “variables” are the same, say if one could move Greece and its grid in the position of Finland). Note however that if one uses another more direct long term earth affecting solar activity index, this time difference gets shorter: for example the max Ap mean, the max Dst mean, the max of annual number of days with Ap ≥ 40 and the max of annual number of days with Dst ≤ −40 for solar cycle 22 they all occurred in 1991 – and not in 1989 as sunspots did – and in this case the phase delay was 2 years and not 4. For solar cycle 23, the max Ap mean, the max Dst mean, the max of annual number of days with Ap ≥ 40 all occurred in 2003 (yet the max of annual number of days with Dst ≤ −40 occurred in 2002) and not in 2000 as sunspots did and in this case the phase delay was 3 years and not 6. Figure 3 along with the above discussion also explains the negative sign of the correlation coefficient between TFN and SSN (linear regression approximation).
Then we applied various statistical techniques, regression and correlation, using a number of function models: linear, polynomial (of various degrees), logarithmic, exponential and hyperbolic and we computed the corresponding equations (coefficients) and coefficient of determination. We gathered all these regression results in Table 3 (for the global long tern solar activity indices) and in Table 5 (Sect. 4.2) we presented the regression results for the local long term solar activity index (data from Penteli).
Now let us comment on the regression results: The best results (larger coefficient of determination) in all cases were given by polynomials and this is due to the Stone-Weierstrass Theorem from functional analysis.
Another interesting point here is that the highest coefficient of determination (0.35) was obtained using SSN (along with a polynomial of 6th degree). This is perhaps a little surprising since SSN is a global and indirect (for our purposes) index. One might expect that the best results would have been obtained with the local K-index data (direct and local index). The explanation for this fact is, we believe, that the SSN curve is smoother and it complies better with the mathematical requirements of regression (see also below). However, when we push polynomial regression to the limit and we use more sophisticated mathematical tools, the best result (R 2 = 0.88) is obtained by the “direct” index annual number of days with Dst ≤ −40.
We would also like to make a comment on the use of the specific data to define our long term indices: The reason for choosing to rely primarily (but not exclusively) on Ap and Dst data throughout this work (which are planetary averages) is this: There is only one geomagnetic station in Greece, the Penteli Magnetic Observatory. It is understandable that the “slope” ΔB/Δt with Δt ~ 1 min (or the geoelectric field) would be more physically relevant short term geomagnetic local indices.
These local data (ΔB/Δt with Δt ~ 1 min) are not publicly available from the magnetic observatory of Penteli; in fact we are not even sure if they exist for the period of interest (1989–2010) since Penteli became a member of the World Data Centre for Geomagnetism from late 2010 onwards.
As far as the geoelectric field is concerned, we are not aware of any institution in Greece making such measurements.
We would like to mention however that even if these local data were available, one has to bear in mind that the final step would be to use them to define a long term index (on an annual basis). The most obvious choice would be to compute some annual average. It is probable that the “sensitivity” of these short term local indices might be lost when we pass on from short term to the long term. For example if one computed the annual average of the 1 min slope ΔB/Δt, there are half a million minutes in a year and thus this long term index (annual one minute variation of the magnetic field) might be almost constant throughout the 11-year solar cycle. The next step would be to apply statistical regression techniques. These mathematical methods rely on certain mathematical theorems which in turn are based on certain assumptions (the most important ones are that the variables are non-stochastic, weak exogeneity holds, homoscedasticity holds, normality of residuals holds, there is no self-correlation of the residuals, the covariance between the variable values and the error term tends to zero, etc. – we checked some of them for one specific case, the annual average of the daily K-index sum from Penteli); it is not guaranteed that the most physically relevant indices are those which satisfy the mathematical assumptions the most and hence give the largest coefficient of determination (this is the meaning of the phrase in the text that “this is a physics vs. maths game” and that “the SSN time curve has a smoother graph”). As we can see from our results, for example SSN is an indirect earth affecting solar activity index yet nonetheless gives a satisfactory coefficient of determination – perhaps a rather surprisingly satisfactory coefficient of determination. Hence our approach to use statistics and the coefficient of determination as a criterion (which, let us recall does not necessarily mean causation but it does mean predictability according to one of the golden rules in statistics) gives in some sense the optimal result between basically three pairs of opposite parameters: short term vs. long term, physical relevance vs. mathematical convenience, global vs. local geomagnetic data. Needless to say if we had these data we would have run our models for them too.
It is straightforward that the physical quantity which is the most physically relevant for our study are the GICs. The ideal would be to have local measurements for GICs, define some long term index from them and then apply our statistical models between GICs and TFN. Yet these currents have never been measured directly anywhere in Greece during the past and to the best of our knowledge there is no program to do so in the future. It is well known however that there is a good linear approximation between GICs and the geoelectric field (see e.g., Lindahl 2003; Pulkkinen 2003; Viljanen et al. 2004; Pulkkinen et al. 2008, 2010, 2012), given by the following equation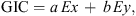 where (a, b) are system-specific parameters typically in the range of 0–200 (in A km/V) and Ex and Ey are the horizontal components of the geoelectric field (y-axis in the east-west direction with the positive y-semi-axis pointing to the east and the x-axis in the south-north direction with the positive x-semi-axis pointing to the north). If no transformer data is known then the values a = b = 50 A km/V can give a good approximation of the sum of GIC flowing over all phases of the transformer. Unfortunately, to the best of our knowledge, there are no measurements of the geoelectric field anywhere in Greece either.
where (a, b) are system-specific parameters typically in the range of 0–200 (in A km/V) and Ex and Ey are the horizontal components of the geoelectric field (y-axis in the east-west direction with the positive y-semi-axis pointing to the east and the x-axis in the south-north direction with the positive x-semi-axis pointing to the north). If no transformer data is known then the values a = b = 50 A km/V can give a good approximation of the sum of GIC flowing over all phases of the transformer. Unfortunately, to the best of our knowledge, there are no measurements of the geoelectric field anywhere in Greece either.
One can compute the geoelectric field from the geomagnetic field (horizontal components Bx, By) using the relations suggested in the literature given above (Lindahl 2003; Pulkkinen 2003; Viljanen et al. 2004; Pulkkinen et al. 2008, 2010, 2012):![$$ {Ex}(\omega )\enspace =\enspace [Z(\omega )\enspace By\enspace (\omega )]/{\mu }_0 $$](/articles/swsc/full_html/2013/01/swsc120058/swsc120058-eq21.gif) and
and ![$$ {Ey}(\omega )\enspace =\enspace [Z(\omega )\enspace {Bx}\enspace (\omega )]/{\mu }_0, $$](/articles/swsc/full_html/2013/01/swsc120058/swsc120058-eq22.gif) where μ
0 is the permeability of the vacuum, ω is the angular frequency of the fluctuating field (about 0.01–0.1 Hz) and Z(ω) denotes the surface impedance which depends on the ground conductivity. These equations are derived from Faraday’s Law making various simplifications. Again, to the best of our knowledge there are no measurements of the surface impedance in Greece.
where μ
0 is the permeability of the vacuum, ω is the angular frequency of the fluctuating field (about 0.01–0.1 Hz) and Z(ω) denotes the surface impedance which depends on the ground conductivity. These equations are derived from Faraday’s Law making various simplifications. Again, to the best of our knowledge there are no measurements of the surface impedance in Greece.
So the key thing is that we believe we did our best with the data available.
Acknowledgments
The author wishes to thank the following people for providing data and for useful discussions: Athanasios Tzortzis (TRSC, PPC Greece), Constantine Mavromatos (IPTO, ADMIE Greece), P. Kapiris, P. Tsailas and G. Filippopoulos (GOP and IGME Greece), Mike Hapgood (RAL, Oxford, UK), Sarah James (UKSSDC, RAL Space, Oxford UK), Hans-Joachim Linthe (Helmholtz Centre Potsdam, Germany), Brent Gordon, Robert Rutledge and William Murtagh (NOAA, Space Weather Prediction Centre, Boulder Colorado, USA) and Masahito Nose (World Data Centre for Geomagnetism, Kyoto, Japan).
References
- Adams, W.G., Comparison of simultaneous magnetic disturbance at several observatories, Phil. Trans. London (A), 183, 131, 1892. [Google Scholar]
- Akasofu, S.-I., and S. Chapman, On the asymmetric development of magnetic storm field in low and middle latitudes, Planet. Space Sci., 12, 607, 1964. [Google Scholar]
- Akasofu, S.-I., and S. Chapman, Solar Terrestrial Physics, Oxford University Press, Oxford, 1972. [Google Scholar]
- Barlow, J.L., Chapter 9: Numerical Aspects of Solving Linear Least Squares Problems. In C.R. Rao, Handbook of statistics – computational statistics, Amsterdam, London, New York, Tokyo, North Holland, p. 920, ISBN: 0-444-88096-8, 1993. [Google Scholar]
- Bartels, J., N.H. Heck, and H.F. Johnston, The three-hour range index measuring geomagnetic activity, Geophys. Res., 44, 411–454, 1939. [Google Scholar]
- Björck, Åke., Numerical methods for least squares problems, SIAM, Philadelphia, 1996. [Google Scholar]
- Bossi, A., J.E. Dind, J.M. Frisson, U. Khoudiakov, H.F. Light, D.V. Narke, Y. Tournier, and J. Verdon, An international survey on failures in large power transformers in service, Cigré Electra, 88, 21–48, 1983. [Google Scholar]
- Broun, J.A., On the horizontal force of the Earth’s magnetism, Proc. Roy. Soc. Edinburgh, 22, 511, 1861. [CrossRef] [Google Scholar]
- Cahill, L.J.., Jr, Inflation of the inner magnetosphere during a magnetic storm, J. Geophys. Res., 71, 4505, 1966. [CrossRef] [Google Scholar]
- Campbell, W.H., Introduction to Geomagnetic Fields, Cambridge University Press, 2002. [Google Scholar]
- Carlowicz, M., and R. Lopez, Storms from the Sun, National Academies Press, 2002. [Google Scholar]
- Chambers, J.M., and T.J. Hastie, Statistical Models in S. Wadsworth & Brooks/Cole, 1992. [Google Scholar]
- Chapman, S., The electric current-systems of magnetic storms, Terr. Mag. Atomos. Phys., 40, 349, 1935. [CrossRef] [Google Scholar]
- Chapman, S., and V.C.A. Ferraro, A new theory of magnetic storms, Nature, 129, 3169, 1930. [Google Scholar]
- Chapman, S., The morphology of magnetic storms: an extension of the analysis of Ds, the disturbance local-time inequality, Annali di Geofisica, 5, 481, 1952. [Google Scholar]
- Coetzee, G., and C.T. Gaunt, Transformer failures in regions incorrectly considered to have low GIC-risk, APAN (All Partners Access Network), US Department of Defence, https://community.apan.org/space_weather_task_force/m/mediagallery/107001.aspx, 2007. [Google Scholar]
- Cohen, J., P. Cohen, S.G. West, and L.S. Aiken, Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 2nd ed. Lawrence Erlbaum Associates, Hillsdale, NJ, 2003. [Google Scholar]
- Crooker, N.U., and G.L. Siscoe, Birkeland currents as the cause of the low-latitude asymmetric disturbance field, J. Geophys. Res., 86, 11201, 1981. [CrossRef] [Google Scholar]
- Daniel, W.W., and J.C. Terrell, Business Statistics for Management & Economics, Houghton Mifflin, 1995. [Google Scholar]
- Draper, N.R., and H. Smith, Applied Regression Analysis, Wiley Series in Probability and Statistics, 3rd ed., ISBN: 978-0-471-17082-2, 1998. [Google Scholar]
- Dessler, A.J., W.E. Francis, and E.N. Parker, Geomagnetic storm sudden – commencement rise times, J. Geophys. Res., 65, 9, 1960. [CrossRef] [Google Scholar]
- Frank, L.A., Direct detection of asymmetric increases of extraterrestrial ring proton intensities in the outer radiation zone, J. Geophys. Res., 75, 1263, 1970. [CrossRef] [Google Scholar]
- Fukushima, N., and Y. Kamide, Partial ring current models for world geomagnetic disturbances, Rev. Geophys. Space Phys., 11, 795, 1973. [Google Scholar]
- Gaunt, C.T., and J. Kohen, Geomagnetically Induced Currents at Mid-Latitudes, Proceedings of the XXVIIth URSI General Assembly in Maastricht, see http://www.ursi.org/Proceedings/ProcGA02/papers/p1065.pdf, 2009. [Google Scholar]
- Glicksberg, I., Measures Orthogonal to Algebras and Sets of Antisymmetry, Trans. Am. Math. Soc., 105 (3), 415–435, 1962. [CrossRef] [Google Scholar]
- Goodall, C.R., Chapter 13: Computation using the QR decomposition. In C.R. Rao, Handbook of Statistics – Computational Statistics, Amsterdam, London, New York, Tokyo, North Holland, p. 852, ISBN: 0-444-88096-8, 1993. [Google Scholar]
- Hamilton, D.C., G. Gloeckler, F.M. Ipavich, W. Stüdemann, B. Wilken, and G. Kremser, Ring current development during the great geomagnetic storm of February 1986, J. Geophys. Res., 93, 14343, 1988. [CrossRef] [Google Scholar]
- Haymes, Robert C., Introduction to Space Science, Wiley & sons, 1971. [Google Scholar]
- Hess, W.N., The Radiation Belt and Magnetosphere, Blaisdell Publishing Co, 1968. [Google Scholar]
- Jeffreys, H., Weierstrass’s Theorem on Approximations by Polynomials, in Methods of Mathematical Physics, 3rd ed., Cambridge University Press, 1988. [Google Scholar]
- Kallio, E., T.I. Pulkkinen, H.H.J. Koskinen, A. Viljanen, Loading-unloading processes in the nightside ionosphere, J. Geophys. Res., 27, 125, 2000. [Google Scholar]
- Kamide, Y., and W. Baumjohann, Magnetosphere-ionosphere coupling, Physics and Chemistry in Space, 23, 112, 1993. [Google Scholar]
- Kamide, Y., Geomagnetic Storms as a Dominant Component of Space Weather: Classic Picture and Recent Issues. In Space Storms and Space Weather Hazards, Nato Science Series, Ed. I. Daglis (Kluwer Academic Publishers), 43, 2001. [CrossRef] [Google Scholar]
- Kaw, A., and E. Kalu, Numerical Methods with Applications (Chapter 6 deals with linear and non-linear regression), Florida University Press, p. 145, Paperback, ISBN: 978-0-578-05765-1, 2008. [Google Scholar]
- Kennedy Jr, and J.E. Gentle, W.J., Statistical Computing, Marcel Dekker, 1980. [Google Scholar]
- Kertz, W., Ein neues Mass für die Feldstärke des erdmagnetischen aquatorialen Ringstroms, Abh. Akad. Wiss. Göttingen Math. Phys., 2, 83, 1958. [Google Scholar]
- Kertz, W., Ring current variations during the IGY, Ann. Int. Geophys., 35, 49, 1964. [Google Scholar]
- Kivelson, M., and C. Russell, Introduction to Space Physics, Cambridge University Press, 1995. [Google Scholar]
- Koen, J., and C.T. Gaunt, Disturbances in the Southern African power network due to geomagnetically induced currents, Cigré Session, Paper 36-206, Paris, 2002. [Google Scholar]
- Langel, R.A., R.H. Estes, G.D. Mead, E.B. Fabiano, and E.R. Lancaster, Initial geomagnetic field model from Magsat vector data, Geophys. Res. Lett., 7, 793, 1980. [CrossRef] [Google Scholar]
- Langel, R.A., J. Berbert, T. Jennings, and R. Horner. Magsat data processing: a report for investigators, NASA Technical Memorandum 82160, Goddard Space Flight Center, 1981 [Google Scholar]
- Lehtinen, M., and R. Pirjola, Currents produced in earthed conductor networks by geomacnetically induced electric fields, Ann. Geophys., 3, 4, 1985. [Google Scholar]
- Lindahl, S., Effects of geomagnetically induced currents on protection systems, Elforsk Report 03:34, Elforsk AB, Stockholm, Sweden [Google Scholar]
- Mayaud, P.N., Derivation, Meaning, and Use of Geomagnetic Indices, Geophysical Monograph 22, American Geophysical Union, Washington, DC, 1980. [Google Scholar]
- Minhas, M.S.A., J.P. Reynders, and P.J. De Klerk, Failures in power system transformers and appropriate monitoring techniques, Proc. 11th International Symposium on High Voltage Engineering (Conf. Publ. No 467), London, Vol. 1, pp. 94–97, 1999. [Google Scholar]
- Moos, N.A.F., Magnetic observations made at the government observatory, Bombay, for the period 1846 to 1905, and their discussion, Part II: the phenomenon and its discussion, Bombay, 1910. [Google Scholar]
- Nievergelt, Y., Total least squares: state-of-the-art regression in numerical analysis, SIAM Rev., 36 (2), 258–264, 1994. [CrossRef] [Google Scholar]
- Parks, George K., Physics of Space Plasmas “1”: An Introduction, Addison-Wesley, 1991. [Google Scholar]
- Pedhazur, E., Multiple Regression in Behavioral Research: Explanation and Prediction, 2nd ed., Holt, Rinehart and Winston, New York, 1982. [Google Scholar]
- Pindyck, R.S., and D.L. Rubinfeld, Econometric Models and Economic Forecasts, ch. 1 (Introduction including appendices on Σ operators & derivation of parameter estimations) & Appendix 4.3 (multiple regression in matrix form), 4th ed., 1998. [Google Scholar]
- Price, P.R., Geomagnetically induced current effects on transformers, IEEE Trans. Power Delivery, 17 (4), 1002–1008, 2002. [CrossRef] [Google Scholar]
- Pulkkinen, A., Geomagnetic Induction During Highly Disturbed Space Weather Conditions: Studies of Ground Effects, Finnish Meteorological Institut, Helsinki, Finland, 2003. [Google Scholar]
- Pulkkinen, A., R. Pirjola, D. Boteler, A. Viljanen, and I. Yegorov, Modelling of space weather effects on pipelines, J. Appl. Geophys., 48, 233, 2001a. [Google Scholar]
- Pulkkinen, A., A. Viljanen, K. Pajunpaa, and R. Pirjola, Recordings and occurrence of geomagnetically induced currents in the Finnish natural gas pipeline network, J. Appl. Geophys., 48, 219, 2001b. [Google Scholar]
- Pulkkinen, A., O. Amm, A. Viljanen, and BEAR Working Group, Ionospheric equivalent current distributions determined with the method of spherical elementary current systems, J. Geophys. Res., 108, DOI: 10.1029/2001JA005085, 2003a. [Google Scholar]
- Pulkkinen, A., A. Thomson, E. Clarke, and A. McKay, April 2000 geomagnetic storm: ionospheric drivers of large geomagnetically induced currents, Ann. Geophys., 21, 709, 2003b. [Google Scholar]
- Pulkkinen, A., O. Amm, A. Viljanen, and BEAR Working Group, Separation of the geomagnetic variation field on the ground into external and internal parts using the spherical elementary current system method, Earth, Planets Space, 55, 117, 2003c. [Google Scholar]
- Pulkkinen, A., R. Pirjola, and A. Viljanen, Statistics of extreme geomagnetically induced current events, Space Weather, 6, S07001, 2008. [CrossRef] [Google Scholar]
- Pulkkinen, A., M. Hesse, H. Shahid, L. Van der Zel, B. Damsky, F. Policelli, D. Fugate, W. Jacobs, and E. Creamer, Solar shield: forecasting and mitigating space weather effects on high-voltage power transmission systems, Nat Hazards, 53, 333–345, 2010. [Google Scholar]
- Pulkkinen, A., E. Bernaneu, J. Eichner, C. Beggan, and A. Thomson, Generation geomagnetically induced current scenarios, Submitted, 2012. [Google Scholar]
- Rangarajan, G.K., Indices of Geomagnetic Activity. In Geomagnetism, Ed. J.A. Jacobs (Academic Press, London), p. 323, 1989. [Google Scholar]
- Rostoker, G., Geomagnetic Indices, Rev. Geophys. Space Phys., 10, 157, 1972. [CrossRef] [Google Scholar]
- Rudin, W., Principles of Mathematical Analysis, 3rd. ed., McGraw-Hill, 1976. [Google Scholar]
- Schrijver, C.J., and S.D. Mitchell, Disturbances in the US electric grid associated with geomagnetic activity, J. Space Weather Space Clim., 3, A19, http://dx.doi.org/10.1051/swsc/2013041, 2013. [CrossRef] [EDP Sciences] [Google Scholar]
- Shapiro, S.S., and M.B. Wilk, An analysis of variance test for normality (complete samples), Biometrica, 52 (3–4), 591–611, 1965. [Google Scholar]
- Shelley, E.O., Heavy ions in the magnetosphere, Space Sci. Rev., 23, 465, 1979. [CrossRef] [Google Scholar]
- Smith, P.H., N.K. Bewtra, and R.A. Hoffman, Inference of the ring current ion composition by means of charge exchange decay, J. Geophys. Res., 86, 34–70, 1981. [Google Scholar]
- Snedecor, G.W., and W.G. Cochran, Statistical Methods, 8th ed., Iowa State University Press, 1989. [Google Scholar]
- Sugiura, M., Dst Index, http://wdc.kugi.kyoto-u.ac.jp/dstdir/, 1991. [Google Scholar]
- Sugiura, M., and S. Hendricks, Provisional hourly values of equatorial Dst for 1961, 1962 and 1963, NASA Tech. note D-4047, 1967. [Google Scholar]
- Takasu, N., T. Oshi, F. Miyawaki, S. Saito, and Y. Fujiwara, An experimental analysis of DC excitation of transformers by geomagnetically induced currents, IEEE Trans. Power Delivery, 9, 1173–1179, 1994. [Google Scholar]
- Tascione, Thomas.F., Introduction to the Space Environment, 2nd ed., Kreiger, Malabar, FL, 1994. [Google Scholar]
- Tsunomura, S., Characteristics of geomagnetic sudden commencement observed in middle and low latitudes, Earth, Planets, Space, 50, 1998. [Google Scholar]
- Tsurutani, B., and W. Gonzalez, The interplanetary causes of magnetic storms: a review, Magnetic Storms, AGU Geophysical Monograph, 98, 1997. [CrossRef] [Google Scholar]
- United States National Academy of Sciences Report, Severe Space Weather Events – Understanding Societal and Economic Impacts Workshop Report, http://www.nap.edu/catalog.php?record_id=12507, 2008. [Google Scholar]
- United Kingdom Royal Academy of Engineering, Extreme Space Weather: impacts on engineered systems and infrastructure, http://www.raeng.org.uk/news/publications/list/reports/Space_Weather_Full_Report_Final.PDF, 2013. [Google Scholar]
- Van Allen James, A., Origins of Magnetospheric Physics, Smithsonian Institution Press, 1983. [Google Scholar]
- Venables, W.N., and D.M. Smith, An Introduction to R (On line Notes on R), http://cran.r-project.org/doc/manuals/R-intro.pdf, 2013. [Google Scholar]
- Vestine, E.H., L. Laporte, I. Lange, and W.E. Scott, The geomagnetic field, its description and analysis, Carnegie Institution of Washington Publication, Washington DC, p. 580, 1947. [Google Scholar]
- Viljanen, A., A. Pulkkinen, O. Amm, R. Pirjola, and T. Korja, Fast computation of the geoelectric field using method of elementary current system and planar earth models, Ann. Geophys., 22, 101–113, 2004. [Google Scholar]
- Walt, M., Introduction to Geomagnetically Trapped Radiation, Cambridge University Press, New York, NY, 1994. [CrossRef] [Google Scholar]
- Williams, D.J., Ring Current Composition and Sources. In Dynamics of the Magnetosphere, Ed. S.-I., Akasofu (D. Reidel Publishing Company), p. 407, 1980. [Google Scholar]
- Williams, D.J., Ring current composition and sources: an update, Planet. Space Sci., 29, 1195, 1981. [CrossRef] [Google Scholar]
- Zois, I.P., A new invariant for σ-models, Commun. Math. Phys., 209, 757–783, 2009. [Google Scholar]
- Zois, I.P., 18 Lectures on K-Theory, arxiv.org 1008.1346, 2010. [Google Scholar]
- Zois, I.P., Solar activity and transformer failures in the Greek national electric grid I: Linear phenomena, talk given during the 8th European Space Weather Week-Session 3A, GIC Advances and Developing Mitigation Procedures, 28 Nov–2 Dec, Namur, Belgium, 2011. [Google Scholar]
- Zois, I.P., The Effects of solar Activity onto Transformers in the Greek National Electric Grid (Part II: Non-linear phenomena), 9th European Space Weather Week, 5–9 Nov, Brussels, Belgium, Académie Royale de Belgique, http://www.stce.be/esww9/program/poster1.php, 2012. [Google Scholar]
- Zois, I.P., Modeling the effects of solar activity on the Greek National Electric Grid, International Conference on Mathematical Modeling in Physical Sciences, 1–5 September, Prague, Czech Republic, http://www.icmsquare.net/index.php?option=com_sessions&view=program&Itemid=85, 2013a. [Google Scholar]
- Zois, I.P., Solar Activity and Transformer Failures in Greece (3): New Results on non Linear Regression Analysis, Developing Societal Resilience Against Space Weather 10th European Space Weather Week, 18–22 Nov, Antwerp, Belgium, http://www.stce.be/esww10/sessions/02resilience.php, 2013b. [Google Scholar]
- Zois, I.P., Solar Activity and Transformer Failures in the Greek National Electric Grid, [arXiv: 1307.1149], 2013. [Google Scholar]
Cite this article as: Zois I.P.: Solar activity and transformer failures in the Greek national electric grid. J. Space Weather Space Clim., 2013, 3, A32.
All Tables
Residuals of polynomial of order six curve (annual average of daily K-index sum vs. TFN).
All Figures
 |
Figure 1. Long term solar activity indices (all scaled except SSN) vs. Time graph. |
| In the text | |
 |
Figure 2. SSN vs. TFN scatter plot. |
| In the text | |
 |
Figure 3. (Scaled) TFN and SSN vs. Time graph. The blue curve is SSN, the red curve is the (scaled) TFN and the green curve is the smoothed (and scaled) TFN. |
| In the text | |
 |
Figure 4. SSN (blue) and scaled (multiplied by a factor of 95) Annual mean of the daily K-index sum from Penteli (purple) vs. Time graph. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.