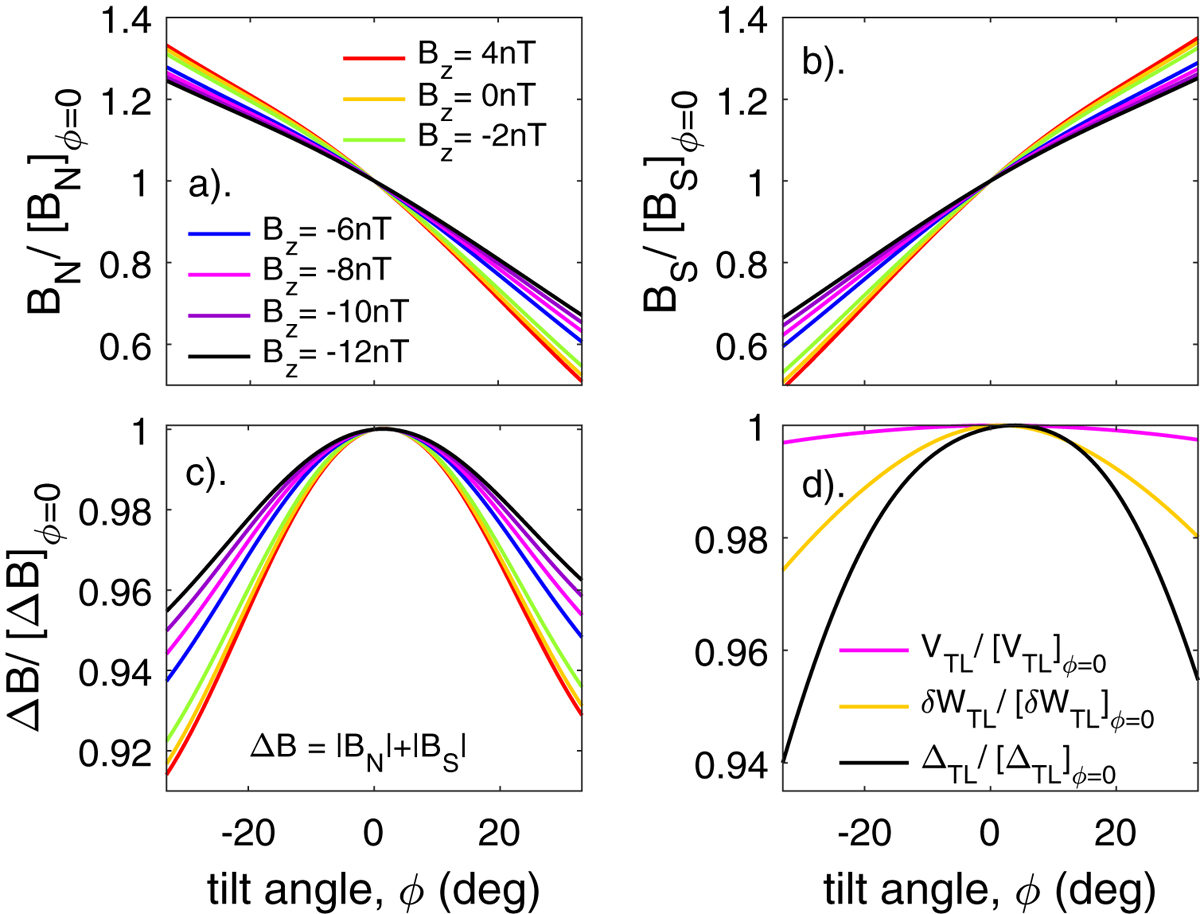
(Top panels) The maximum lobe field along the bisector of the tail hinge angle, evaluated assuming ω = B ²/2μ _o and shown as a function of the dipole tilt angle ϕ and for various values of the IMF B _z. (a) shows the field in the northern lobe, B _N, (b) shows that in the southern lobe, B _S, both as a ratio of their values for ϕ = 0. The fall in B _N with increasing ϕ is mirrored by a rise in B _S, but not quite exactly: this can be seen in part (c) that shows the magnetic shear across the hinge in the current sheet ΔB = |B _N| + |B _S| which is proportional to the current per unit length in the cross-tail current sheet (again plotted values are normalized to the value for ϕ = 0, [ΔB] _ϕ=0. It can be see that ΔB is largest for ϕ = 0 but is also larger for large positive ϕ than large negative ϕ. This is another consequence of the hemispheric asymmetry in the magnetopause model. Part (d) looks at the dependence on ϕ of the difference between the results for IMF B _z = −6 nT and B _z = 0 of: the total volume of the tail between X _GSE = −50 R _E and X _GSE = 0, V _TL; the rise in total stored energy compared to IMF B _z = 0 case, δW _TL (which is the integral of δω over the volume V _TL); and the fractional rise in total energy compared to the B _z = 0 case, Δ_TL = δW _TL/[W _TL]_Bz=0. Each is again plotted normalized to its value for ϕ = 0 to allow comparisons of the effects of ϕ which in each case shows the same general form as the variation of the magnetic shear, with largest values for ϕ = 0, but slightly larger values for large positive ϕ than for correspondingly large negative ϕ.