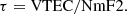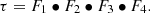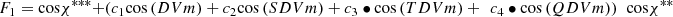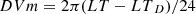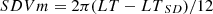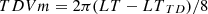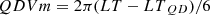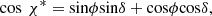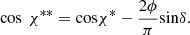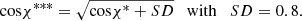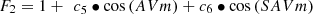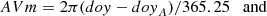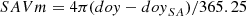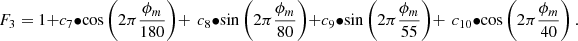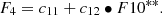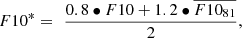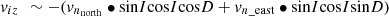| Issue |
J. Space Weather Space Clim.
Volume 11, 2021
|
|
|---|---|---|
| Article Number | 10 | |
| Number of page(s) | 18 | |
| DOI | https://doi.org/10.1051/swsc/2020083 | |
| Published online | 02 February 2021 | |
Research Article
Global equivalent slab thickness model of the Earth’s ionosphere
Institute for Solar-Terrestrial Physics, German Aerospace Center, Kalkhorstweg 53, 17235 Neustrelitz, Germany
* Corresponding author: Norbert.Jakowski@dlr.de
Received:
2
October
2020
Accepted:
30
December
2020
The shape of the vertical electron density profile is a result of production, loss and transportation of plasma in the Earth’s ionosphere. Therefore, the equivalent slab thickness of the ionosphere that characterizes the width of vertical electron density profiles is an important parameter for a better understanding of ionospheric processes under regular as well as under perturbed conditions. The equivalent slab thickness is defined by the ratio of the vertical total electron content over the peak electron density and is therefore easy to compute by utilizing powerful data sources nowadays available thanks to ground and space based GNSS techniques. Here we use peak electron density data from three low earth orbiting (LEO) satellite missions, namely CHAMP, GRACE and FORMOSAT-3/COSMIC, as well as total electron content data obtained from numerous GNSS ground stations. For the first time, we present a global model of the equivalent slab thickness (Neustrelitz equivalent Slab Thickness Model – NSTM). The model approach is similar to a family of former model approaches successfully applied for total electron content (TEC), peak electron density NmF2 and corresponding height hmF2 at DLR. The model description focuses on an overall view of the behaviour of the equivalent slab thickness as a function of local time, season, geographic/geomagnetic location and solar activity on a global scale. In conclusion, the model agrees quite well with the overall observation data within a RMS range of 70 km. There is generally a good correlation with solar heat input that varies with local time, season and level of solar activity. However, under non-equilibrium conditions, plasma transport processes dominate the behaviour of the equivalent slab thickness. It is assumed that night-time plasmasphere–ionosphere coupling causes enhanced equivalent slab thickness values like the pre-sunrise enhancement. The overall fit provides consistent results with the mid-latitude bulge (MLB) of the equivalent slab thickness, described for the first time in this paper. Furthermore, the model recreates quite well ionospheric anomalies such as the Night-time Winter Anomaly (NWA) which is closely related to the Mid-latitude Summer Night-time Anomaly (MSNA) like the Weddell Sea Anomaly (WSA) and Okhotsk Sea Anomaly (OSA). Further model improvements can be achieved by using an extended model approach and considering the particular geomagnetic field structure.
Key words: ionosphere / equivalent slab thickness / modelling / GNSS radio occultation / ionospheric anomalies
© N. Jakowski & M.M. Hoque, Published by EDP Sciences 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The equivalent slab thickness τ describes the shape, more precisely the width of vertical electron density profiles of the ionosphere. It is defined by the ratio of the vertical total electron content (VTEC) and the peak electron density NmF2 according to
The shape of the vertical electron density profile reflects the complexity of production, loss and transportation of plasma in the Earth’s ionosphere. Thus, the equivalent slab thickness τ is very sensitive to the competition of plasma driving forces such as thermospheric winds and electric fields. Hence, this parameter is very helpful in exploring perturbation processes in the ionosphere. Besides vertical plasma redistribution processes, the width or shape of the vertical electron density profile is also sensitive to changes of temperature and composition in the thermosphere.
The behaviour of the equivalent slab thickness has been discussed in many publications since the earliest days of VTEC measurements, e.g. via radio beacon measurements (Titheridge, 1973; Davies et al., 1976; Jakowski et al., 1981; McNamara & Smith, 1982). When dual frequency measurements of the global positioning system (GPS) became available, a new age for estimating the equivalent slab thickness started via vertical sounding station sites (e.g. Breed et al., 1997; Miro et al., 1999; Jayachandran et al., 2004). Nowadays, besides GPS, even more global navigation satellite systems (GNSS) such as GLONASS, Galileo or Beidou are available for estimating TEC on global scale. Since the equivalent slab thickness is closely related to the less variable thermospheric scale height, thermospheric cooling might be studied in a direct way (Jakowski et al., 2017). It is worth noting that there is a remarkable difference between former VHF Faraday rotation beacon studies and newer GNSS-based estimations of the equivalent slab thickness. Due to the radially decreasing magnetic field weighting of Faraday rotation measurements at linearly polarized VHF signals from geostationary satellites, the derived TEC refers to a range up to about 2000 km (Jakowski & Kugland, 1982), whereas GNSS-based estimates of TEC refer to the full range up to satellite heights, thus fully including the plasmasphere. This fact usually leads to mostly higher variable values of the equivalent slab thickness than observed in former beacon studies, in particular when the ionospheric ionisation is low. Thus, as will be discussed later, GNSS-based estimates of τ have to consider the plasmaspheric contribution, in particular at night and under low solar activity conditions.
Further remarkable progress in estimating the equivalent slab thickness on a global scale was achieved when GNSS ionospheric radio occultation (IRO) measurements provided huge data sets of peak electron density NmF2 all over the globe (Hajj & Romans, 1998; Jakowski et al., 2002; Jakowski, 2005). Combining GNSS-based TEC with IRO-derived NmF2, climatological studies of the equivalent slab thickness are possible (e.g. Huang & Yuan, 2015; Fang et al., 2018). Both these data sources have a high potential to further explore the ionosphere–thermosphere–plasmasphere relationships.
It has been shown that the equivalent slab thickness is a valuable parameter for exploring the dynamics of plasma redistribution processes inside the ionosphere, e.g. during heavy storms or solar eclipses (Jakowski et al, 1981, 2008, 2015; Jakowski & Förster, 1995; Förster & Jakowski, 1988; Hoque et al., 2016). In addition, equivalent slab thickness also helps to better understand ionosphere–plasmasphere and thermosphere–ionosphere coupling processes (e.g. Jakowski et al., 1991a, 2015, 2017; Jakowski & Hoque, 2018).
Due to the simple relationship (1) the equivalent slab thickness can principally be used to derive NmF2 from VTEC data (Gerzen et al., 2013; Maltseva & Mozhaeva, 2016a) or vice versa to derive VTEC from NmF2 data (e.g. Fox et al., 1991). Therefore, several attempts have been made to develop models of the equivalent slab thickness for this purpose. Most empirical model approaches are limited to the site of vertical sounding stations, specific regions or selected time periods. Fox et al. (1991) developed a mid-latitude slab thickness model for Hamilton, Massachusetts, based on Faraday rotation measurements. Maltseva & Mozhaeva (2016b) tried to develop a global model of the equivalent slab thickness based on a so-called hyperbolic approximation closely related to NmF2. Two coefficients have been derived from median values of the equivalent slab thickness and related NmF2 data at different longitude sectors for March 2015. A simple approach to model the equivalent slab thickness could be a combination of values obtained from individual TEC and NmF2 models as performed by Gerzen et al. (2013) using the models Neustrelitz TEC Model (NTCM, Jakowski et al., 2008) and Neustrelitz Peak Density Model (NPDM, Hoque & Jakowski, 2011) developed at DLR. In a similar way, Muslim et al. (2015) has developed a global model for the equivalent slab thickness that is based on simple sub-models for TEC and the critical frequency of the ionospheric F2 layer foF2. However, such sub-model approaches smooth out special peculiarities of the equivalent slab thickness thus ignoring its high variability. Up to now, a closed form of an empirical global slab thickness model doesn’t exist, probably due to the high variability of the slab thickness and resulting difficulties.
Studying day-to-day variability of NmF2, Rishbeth & Mendillo (2001) concluded that NmF2 has a day-to-day standard deviation of 20 to 33% under moderate solar activity conditions characterized by approximately 140 units of the solar 10.7 cm radio flux index F10. Forbes et al. (2000) reported a variability of NmF2 in the order of 10 to 30% relative to mean values. The studies show that the short-term variability of NmF2 is primarily related to the geomagnetic activity and partially also to meteorological sources from the lower atmosphere. Under magnetically disturbed conditions the variability of NmF2 may increase by a factor of two. Fang et al. (2018) report variability values for TEC and NmF2 in the order of 15–25%. As it is defined by the ratio of TEC and NmF2, τ reacts very sensitively to changes of one of these parameters or a combination of them. So, it is evident that the variability of τ may reach 50% or even more. For instance, Jayachandran et al. (2004) report a variability of up to 67% by night at mid-latitudes in summer.
In addition to high dynamic ionospheric processes, also measurement errors of TEC (Hoque & Jakowski, 2013) and NmF2 quantities (Lei et al., 2007; Schreiner et al., 2007) contribute to uncertainties of the equivalent slab thickness. During ionospheric storms, TEC and NmF2 may even vary in an opposite direction due to competing driving forces like electromagnetic drift and thermospheric winds (Jakowski, 1981). Such highly dynamic processes in the ionosphere lead to extreme variations of the equivalent slab thickness (e.g. Jakowski et al., 1981, 1990a). Nevertheless, despite this a-priori difficulty in modelling, encouraged by the good performance of earlier models developed in DLR for TEC, NmF2, hmF2 and plasmasphere (Hoque & Jakowski, 2011, 2012; Jakowski et al., 2011a; Jakowski & Hoque, 2018), we here apply a similar efficient and robust modelling approach to describe the behaviour of the equivalent slab thickness τ at a global scale and for any level of solar activity in a closed form with only a few coefficients. To avoid smoothing effects caused by a combination of sub-models for TEC and NmF2, we intend to model the equivalent slab thickness from original locally computed τ values.
When developing this model, we have focused on a good overall description of τ, being aware of the big diversity of τ in general. Hence, because τ is a sensitive ratio and depends on many impact factors, the accuracy of the model in specialized applications is of secondary importance here. Estimating the peak electron density from VTEC measurements via a slab thickness model is possible, vice versa also VTEC can be estimated from NmF2 data via a slab thickness model. However, one should be aware that the high natural variability of τ generally limits the accuracy of model- based estimations of these quantities.
2 Modelling database
As stated in (1), the slab thickness is defined as the ratio of the vertical total electron content and the peak electron density NmF2. As input for NmF2 we have used space-based ionospheric radio occultation (IRO) measurements and ground-based vertical sounding measurements from ionosondes. The IRO data are used in the slab thickness model development, whereas the ionosonde data are used for model validation. The IRO-derived NmF2 data from three low earth orbiting (LEO) satellite missions, namely CHAMP (CHAllenging Minisatellite Payload), GRACE (Gravity Recovery And Climate Experiment) and FORMOSAT-3/COSMIC (Constellation Observing System for Meteorology, Ionosphere, and Climate), are used. The CHAMP and GRACE data cover early time periods from 2001 to 2008 and 2008 to 2010, respectively, whereas the FORMOSAT-3 data cover the period from 2006 to 2018. Thus, the database covers high and low solar activity conditions from the previous and current solar cycle, 23 and 24. The COSMIC/FORMOSAT-3 satellite constellation of six microsatellites provided much more IRO observations compared to the single satellite CHAMP mission. The successor of COSMIC/FORMOSAT-3, namely the COSMIC-2/FORMOSAT-7 constellation of six satellites was launched on 25 June 2019. The used CHAMP and GRACE IRO data are processed by the German Aerospace Center (DLR, for details see Jakowski et al., 2002; Jakowski, 2005) available at https://isdc.gfz-potsdam.de/champ-isdc/access-to-the-champ-data/ (last accessed on 08.08.2020). The FORMOSAT-3 data are processed by UCAR’s (University Corporation for Atmospheric Research) COSMIC Data Analysis and Archival Center (CDAAC) and made available at https://cdaac-www.cosmic.ucar.edu/ (last accessed on 08/08/2020). It is worth mentioning that near polar orbits of CHAMP, GRACE and FORMOSAT-3 satellites in combination with the daily rotation of the Earth extend the data coverage over the globe. Thus, the used IRO data include different geophysical conditions representing day and night, summer, winter and equinoxes at high, medium and low latitudes.
The source of NmF2 data used in slab thickness model validation is vertical sounding measurements monitored by ionosondes. These observations typically provide the estimation of the critical frequency of the ionosphere (e.g., foF2). The peak electron density NmF2 can be obtained from the critical frequency measurements by NmF2 = 1.24 × 10−2 (foF2)2 in International System units (SI).
The critical frequency data for northern hemispheric stations at Tromsø, Juliusruh and Rome were collected from NOAA’s (National Oceanic and Atmospheric Administration) NGDC (National Geophysical Data Center) site. The critical frequency data for southern hemispheric stations at Townsville and Hobart were collected from the Australian Government Bureau of Meteorology, Space Weather Services.
As a source of global VTEC data we used TEC maps generated by the Center for Orbit Determination in Europe (CODE). The data in IONEX (Ionosphere Map Exchange) format were obtained from the International GNSS Service (IGS) data archive. For estimating slab thickness, the corresponding VTEC values for the IRO measurement location and an ionospheric pierce point (IPP) height of 450 km are computed using IGS-recommended spatial and temporal interpolation methods (Schaer et al., 1998).
The IGS stations are mainly distributed over land areas and station distribution is not homogeneous over all continents. The data coverage over Europe and America is denser than that over Asia and Africa. Again, data are mostly missing over the oceans. Although the CODE TEC maps provide TEC values all over the globe, the quality is expected to degrade over the regions where hardly any data are available. Considering this, we investigated the location of IGS stations used in CODE TEC map generation and identified geographic regions around each station defined by the 10° elevation angle circle at the IPP height. Such regions were identified for each day over the complete period 2001–2018 based on station lists provided in the IONEX file. Note that the slab thickness values were computed combining the TEC and IRO data (see Eq. (1)) only over those regions.
As slab thickness is defined as the quotient of these two independent parameters, it is very sensitive when either VTEC or NmF2 is very small. Our intention is to develop a climatological model, so we have assumed that slab thickness values lie within the range 100–1000 km. The values outside this range are ignored in the model development. The next step is to reduce the size of input data vectors in order to simplify the computational complexity in the fitting procedures. Therefore, the database has been sorted and averaged with respect to solar radio flux variation, seasonal variation, local time variation and geomagnetic latitude and longitude variations. The slab thickness values are averaged for 27 day intervals and the 14th day is taken as the reference day. Similarly, the values are sorted and averaged considering the spatial resolutions 5° meridional (geographic latitude) and 15° zonal (geographic longitude). The local time resolution is restricted to 1 hour.
The driving parameter of the Neustrelitz Slab Thickness Model (NSTM) which is the daily F10.7 is obtained from NOAA’s NGDC site.
3 Basic modelling approach
Due to the close relationship of τ with TEC and the peak electron density NmF2, it is evident that the equivalent slab thickness varies with latitude, season and solar activity (e.g. Titheridge, 1973; Jakowski et al., 1981; Miro et al., 1999; Jayachandran et al., 2004). Consequently, for developing a global model of the equivalent slab thickness we follow the basic NTCM (Neustrelitz TEC Model) approach used for global TEC modelling as described by Jakowski et al. (2011a) or the Neustrelitz Peak Density Model (NPDM) described by Hoque & Jakowski (2011). The challenge for developing an equivalent slab thickness model is its high variability as already mentioned in Section 1. Being aware of this high natural variability, the model approach presented here provides a climatologic estimation of the equivalent slab thickness at global scale under moderate geophysical conditions, ignoring geomagnetic activity effects.
The different terms describing the dependences from local time, season, geomagnetic field and solar activity are combined in a multiplicative way as
The main dependences of τ are described by the factors Fi which implicitly contain the model functions and coefficients.
The variation with the local time (LT in hours) is split into diurnal (D), semidiurnal (SD), terdiurnal (TD), and quadiurnal (QD) harmonic components. The model function describing the local time variation is expressed by
with fixed phase values for the variations
The delayed response of the ionosphere/thermosphere system to the daily solar excitation is taken into account by the phase shift LTD. In a first approach we put LTD = 2, i.e. a delayed response of about 2 hours around noon is assumed. Similarly, we use LTSD = 9, LTTD = 4, and LTQD = 6.
The solar zenith angle at local noon χ*is given by
where φ is the geographic latitude in radians and δ is the declination of the sun.
In a further modification we consider
Finally, the hemispherical asymmetry is considered by the term
The dependence from annual (AV) and semiannual (SAV) variation is defined by
with
The phase shifts doyA = 340 and doySA = 360 are taken from separate pre-studies.
Considering the latitudinal dependence of the equivalent slab thickness as seen later in Figure 14, we use the following approach for incorporating the geomagnetic latitude φm
In order to avoid uncertainties introduced by perturbations occurring often at high latitudes, the fitting procedure is confined to the range 75° S < φm < 75° N.
The dependence from the solar activity is considered via the 10.7 cm solar radio flux index F10 measured in solar flux units (1 sfu = 10−22 Wm−2s−1). In a first step we follow a linear approach as used in previous modelling approaches, but modify the input quantity to an effective radio flux value F10** in two further steps:
Averaging the actual data with the previous three solar rotation averaged F10 values is essential in particular for the equivalent slab thickness, which is closely related to slowly developing temperature and composition changes in the thermosphere as our previous trend studies have shown (Jakowski et al., 2017). Hence, set
where 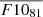 is the 81-day moving average of F10. In addition to this approach, we modify F10 according to observations shown later in Figure 2 which indicate that the equivalent slab thickness increases in antiphase with solar activity at values below F10 = 90. This is unexpected because a lower solar energy input should further decrease τ due to stronger thermospheric cooling. Considering the observational facts, we fix
is the 81-day moving average of F10. In addition to this approach, we modify F10 according to observations shown later in Figure 2 which indicate that the equivalent slab thickness increases in antiphase with solar activity at values below F10 = 90. This is unexpected because a lower solar energy input should further decrease τ due to stronger thermospheric cooling. Considering the observational facts, we fix
and use this quadratic approach in equation (16) for characterizing the slab thickness dependence from solar activity for solar activity levels F10* < 200 sfu.
The basic model approach is described in equations (2)–(17) and applied to slab thickness data sets for determining the 12 coefficients via non-linear least squares methods. The solution coefficients are given in Table 1.
Optimal set of coefficients.
The estimated coefficients are related to the input data set described in Section 2, i.e., their values may change if a different data set is used. Again, the basic approach contains some fixed parameters and their values might also change when other data sets are used. The relative model residuals, i.e., (model–input) *100/input are found as −7%, 29% and 30% for mean, standard deviation (std) and root mean squared (RMS) estimates, respectively. This observation indicates that the equivalent slab thickness doesn’t depend only on the thermospheric temperature as specifically discussed earlier by Jakowski et al. (2017). The increase of τ with decreasing F10 as seen in Figure 2 indicates the growing influence of the plasmaspheric electron content well represented in TEC. Thus, in other words, due to the close coupling of NmF2 to the photo-production at around 200 km height, with decreasing F10, NmF2 decreases faster than TEC which is supported by the more stable plasmaspheric content in particular at a low ionization level during low solar activity (LSA) conditions.
On the other hand, at extremely high solar activity conditions the plasmasphere content doesn’t increase in the same way as F10, related photo-ionization and NmF2 do. This would lead to a reduction of temperature induced growing of the equivalent slab thickness. Consequently, to avoid this effect when estimating the model coefficients, we keep F10* < 200 for fitting. When interpreting the results, one should be aware of this limitation, which we believe is justified when considering the low number of extreme HSA events. In such cases the model might possibly somewhat overestimate the equivalent slab thickness.
It should be mentioned that besides geomagnetic activity dependences (e.g. Kersley & Hosseinieh, 1976; Jakowski et al., 1990a; Jayachandran et al., 2004) also long-term trends of the equivalent slab thickness as reported and discussed by Jakowski et al. (2017) are not considered here. This would require a more detailed approach beyond the scope of the model presented here.
4 Modelling results
In this section we will compare observations under different solar and geophysical conditions with corresponding modelling results. If possible, we try to explain the physics of underlying ionospheric processes.
To get an overall view of model capabilities, we start the presentation of results and discussion with some fundamental dependences.
The diurnal variation as seen in Figure 1 indicates a rather big difference of τ between day and night. The pre-sunrise enhancement of τ as discussed in many papers (e.g. Jakowski et al. 1981; Jayachandran et al., 2004; Huang et al., 2016) is clearly visible with up to about 180 km higher values than at daytime. The pre-sunrise enhancement of τ indicates a stronger decrease of NmF2 compared to TEC that is closely related to the more stable topside ionosphere and plasmasphere. Just before sunrise photoionization starts in the topside ionosphere thus shifting the TEC/NmF2 ratio towards higher values.
 |
Fig. 1 Overall variation of the equivalent slab thickness as a function of the local time (solid red line) in comparison with model values (dashed blue line). |
The model provides smoothed values with a less sharp peak before sunrise. This is understandable when recalling that all latitudes and all seasons are considered here. It is interesting to note that the model provides a clear daytime peak around noon, nicely corresponding with Chapman’s theory that the equivalent slab thickness correlates with the neutral gas scale height H according to τ = 4.13 H. The model value around noon hereafter corresponds to a globally averaged scale height of H = 77.5 km, which is a reasonable value (e.g. Stankov & Jakowski, 2006). The observation data are slightly different but show also an enhancement at daytime due to thermospheric heating.
In general, an increase of the equivalent slab thickness with increasing solar activity is expected. As Figure 2 shows, this is mostly clear at F10 values > 100. At lower values we found a slight increase of the equivalent slab thickness with decreasing F10 values. This unexpected fact has been reported by other researchers too (e.g. Jayachandran et al., 2004; Duarte-Silva et al., 2015). As already mentioned in the previous section, we assume that under low solar activity conditions the rather stable ionization of the plasmasphere becomes visible in TEC (e.g. Jakowski & Hoque, 2018) leading to a lower reduction of TEC than of NmF2. Very low NmF2 values are seen during night and also under LSA conditions favoring a priori high equivalent slab thickness values. This is also in analogy with the NWA effect that is visible only in LSA years (Jakowski et al., 2015). Downward plasmaspheric fluxes cause a noticeable enhancement of the nighttime ionization only at a rather low ionization level, i.e. under low solar activity conditions.
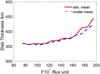 |
Fig. 2 Equivalent slab thickness as a function of solar activity (F10 index). |
The seasonal variation of τ considered in equation (10) is seen in Figure 3. The generalized seasonal variation of the equivalent slab thickness including all data, i.e. also from both hemispheres, are compared with corresponding model values. We see clear peaks in December/January and June/July at nearly the same level of about 365 km. The observed and modelled slab thickness values during the June/July period are slightly higher than in the December/January period. The reason for this difference remains unclear. As Figure 3 shows, there is no significant phase shift of the function with respect to the solstices.
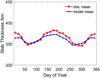 |
Fig. 3 Overall variation of the equivalent slab thickness as a function of the season (red line) in comparison with model values (blue line). |
To answer the question whether different levels of solar activity indicate a quite different behavior of τ, Figure 4 compares its diurnal variation for solar F10 fluxes < 100 and for 120 < F10 < 200 additionally separated for Northern and Southern hemispheres. It is evident that all plots are very similar, indicating only a slight increase of τ under HSA conditions at daytime in agreement with Figure 2. The night-time values are somewhat higher at the Northern hemisphere but the difference is small in all cases. Compared with TEC and NmF2 the variation of τ with the solar activity level is low – a fact that was used by Jakowski et al. (2017) to derive long-term trends of the equivalent slab thickness. Consequently, we will ignore the solar activity dependence in our subsequent discussion. This conclusion is confirmed when considering Figures 5 and 6, where daily averaged global slab thickness maps are shown for LSA and HSA conditions as defined before, for Northern winter and summer, additionally compared with corresponding model maps.
 |
Fig. 4 Diurnal behavior of the equivalent slab thickness at LSA (F10* < 100) and HSA (120 < F10* < 200) conditions averaged over Northern (NH) and Southern hemispheres (SH). |
 |
Fig. 5 Daily averaged global maps of observed and modelled τ for LSA (left) and HSA (right) conditions for Northern summer (NS). |
 |
Fig. 6 Daily averaged global maps of observed and modelled τ for LSA (left) and HSA (right) conditions for Northern winter (NW). |
 |
Fig. 7 Daytime (08–16 LT) seasonally averaged global maps of observed (upper panels) and modelled τ (lower panels) for LSA (left) and HSA (right) conditions. |
Again, LSA and HSA related maps differ only little when considering corresponding hemispheres and seasons. The same is true for the related model maps. Compared to the observations, spatial structure and amplitude values of the model maps are rather smooth, typical for a climatologic model. Considering Figure 8, it is worth noticing that the nighttime values of τ are much more strongly structured in space than the daytime values shown in Figure 7. Due to their higher amplitudes, the patchy structure of nighttime values also dominatess the spatial distribution in the diurnal average as shown in Figures 5 and 6. A first impression indicates a strong geomagnetic control of the slab thickness behavior. Whereas the slab thickness model follows the smooth geomagnetic dipole model equator, the observations follow strictly the real geomagnetic equator and show some pronounced enhancements in the South Atlantic Anomaly (SAA) region.
 |
Fig. 8 Nighttime (20–04 LT) seasonally averaged global maps of observed (upper panels) and modelled τ for LSA and HSA conditions. |
As stated before, all these different maps support the conclusion that the slab thickness depends on solar activity only on a very low level. At daytime there is a positive correlation, whereas at nighttime the equivalent slab thickness is higher at low solar activity level. This observational fact is also reflected in the model as seen in Figures 7 and 8. Observed is a hemispherical imbalance which is probably mainly due to the presence of the geomagnetic SAA in the Southern hemisphere.
5 Validation of NSTM
Before we continue discussing aspects of the slab thickness model NSTM we will check the model at a few selected locations by using vertical sounding (VS) peak electron density values instead of IRO data, i.e. a completely independent data set for NmF2 which includes also methodology aspects. Whereas vertical sounding measurements provide local data over the ionosonde station, IRO data are retrieved from a larger region with a characteristic scale of about 1000 km due to the limb sounding geometry. Consequently, IRO data represent spatially averaged information. Nevertheless, although not identical, IRO and VS data agree quite well as validation studies have shown (Jakowski et al., 2002; Schreiner et al., 2007).
To validate the model approach, we have tested NSTM at 5 vertical sounding stations at different latitudes and hemispheres using data from 2000 to 2008. The station names and coordinates are listed in Table 2.
List of ionosonde stations used for NSTM validation.
The plots in Figures 9–13 show the averaged modelled and observed diurnal variations of the equivalent slab thickness τ for two winter and summer months around the solstices. The corresponding seasonal variations are also depicted.
 |
Fig. 9 Diurnal and seasonal variation of the observed and modelled τ over Tromsø for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
 |
Fig. 10 Diurnal and seasonal variation of the observed and modelled τ over Juliusruh for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
 |
Fig. 11 Diurnal and seasonal variation of the observed and modelled τ over Rome for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
 |
Fig. 12 Diurnal and seasonal variation of the observed and modelled τ over Townsville for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
 |
Fig. 13 Diurnal and seasonal variation of the observed and modelled τ over Hobart for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
Although the variation of model values is smoother and narrower than the one of observed values and variations are sometimes flipped at nighttime, it can be stated that the model lies mostly within the dispersion range of observations (vertical bars). Worst cases are shown at nighttime for mid-latitude ionosonde stations Juliusruh and Rome where the model doesn’t reach the very high values of up to 600 km due to its smoothness. Several attempts to remove this discrepancy within the frame of the current approach failed. Consequently, to bring the model in better agreement with the observations at individual stations, the model approach must be extended. Because the overall conformity is quite good as we have seen in Figures 1–4, we will continue the discussion of model results under physical aspects in the subsequent section.
6 Ionospheric behaviour seen in observations and NSTM
6.1 The mid-latitude bulge of the equivalent slab thickness
The dependence of the equivalent slab thickness on geomagnetic latitude shows very interesting features with several peaks which are persistent in different and partially independent data sets. So, in Figure 14 we see a clear maximum of τ at the geomagnetic equator as expected when considering the solar energy input that peaks at low latitudes. The other peaks are well established in both hemispheres and therefore considered to be the result of systematic processes in the ionosphere. The graphics on the left side indicate a slight asymmetry between Northern and Southern hemispheres. The peaks at high latitudes at around 70° indicate probably Joule heating effects in the aurora zone due to enhanced energy input.
 |
Fig. 14 Variation of the equivalent slab thickness as a function of the geomagnetic latitude (solid red line) in comparison with model values (dashed blue line). Left side: overall data (top) and excluding LSA data (bottom), right side: separated data for summer and winter conditions including both hemispheres. |
An interesting finding is the appearance of secondary peaks at geomagnetic mid-latitudes around 40–45°. We call this effect the mid-latitude bulge (MLB) of equivalent slab thickness. It should be mentioned that NSTM follows this trend in general but smooths out some wider variations.
The geomagnetic mid-latitude peaks reflect obviously significant plasma processes in the ionosphere as underlined in Figure 14 (bottom right) where winter conditions are separated. Here we see that the equivalent slab thickness observations decrease with decreasing solar irradiation, i.e. with decreasing thermospheric heating towards higher latitudes in winter. This effect changes in summer (Fig. 14, top right) when decreasing zenith angle and increasing sunshine duration balance each other towards higher latitudes. The equivalent slab thickness is even slightly higher at high latitudes than at low ones. The mid-latitude peak of τ around at 45° geomagnetic latitude is well pronounced in winter time as Figure 14 clearly shows. This indicates a strong impact of thermospheric meridional winds.
It is well known that the vertical plasma drift viz is very sensitive to thermospheric winds vn according to
with inclination I and declination D of the geomagnetic field (e.g. Rüster, 1971). Since the declination is close to zero at mid-latitudes, the meridional wind term peaks around I = 45° or φm = 45°. This is a strong argument for assuming thermospheric meridional winds as the main driving force for creating the mid-latitude peak of τ.
According to equation (18), an equatorward wind would lift up the plasma, and a poleward wind would shift down the plasma along geomagnetic field lines. Ignoring thermospheric heating effects, two options exist for increasing τ at geomagnetic mid latitudes:
Plasma is lifted up causing enhanced plasmaspheric densities and related TEC.
Plasma is pressed down, leading to a reduction of NmF2 stronger than TEC.
We try to clarify this question in the following discussion. The effectiveness of vertical plasma transport due to meridional thermospheric winds at 250 km height is illustrated in Figure 15. It is evident that the wind induced vertical plasma transport is highest in a zonal band around 45° at both hemispheres, strongly modified by the geomagnetic field structure, in particular obvious near the SAA region.
 |
Fig. 15 Effectiveness of vertical plasma transport due to meridional thermospheric winds at 250 km height. |
If the vertical transport is visible in the slab thickness, which is a ratio of TEC and NmF2 we will check whether the transport effect assumed is also visible in these parameters and additionally in the peak density height hmF2, which directly indicates up or down lifting of plasma.
Indeed, as Figure 16 shows, the vertical transport is not only visible in the equivalent slab thickness but also in other ionospheric key parameters such as TEC, NmF2 and hmF2 during night (20–04 LT). Latitudinal dependences of these variables averaged over both hemispheres are plotted against absolute values of the geomagnetic latitude as a comparison for modelled and observed τ values. All variables indicate a relative peak or plateau at around 40–45° geomagnetic latitudes. The rather small effects in TEC and NmF2 are commonly ignored but become much more pronounced in their ratio, the equivalent slab thickness data. The clear peak of hmF2 data around 45° geomagnetic latitude favors option (1) to explain meridional wind action, i.e. wind induced uplifting of plasma. As the comparison between seasons at the right panels in Figure 14 demonstrates, the uplifting is pronounced in winter time.
 |
Fig. 16 Latitudinal dependences of globally averaged nighttime behavior of equivalent slab thickness, peak electron density NmF2, Peak height hmF2 and vertical total electron content VTEC during winter time, averaged over both hemispheres (time interval: 20–04 LT, years 2001–2018). The equivalent slab thickness observations are compared with corresponding model values (top left, dashed blue line). |
The assumption that the plasma transport is caused by meridional winds is strongly supported by estimations of meridional thermospheric winds for mid-latitude winter conditions by Hedin et al. (1991). Typical diurnal wind profiles obtained from Atmosphere Explorer E and Dynamics Explorer 2 satellites in combination with ground based incoherent scatter radar and Fabry–Pérot optical interferometers are shown for Northern mid-latitudes 30–60 °N in Figure 17.
 |
Fig. 17 Thermospheric winds at mid-latitudes in winter (taken from Hedin et al., 1991). The solid and dashed lines correspond to wind models HWM90 and HWM87, respectively. The different numbers refer to different observation techniques. For further details see Hedin et al. (1991). |
The wind data estimated by various observation techniques clearly indicate equatorward directions at nighttime in winter between 20 and 06 LT. These results have been confirmed by more recent modelling studies on neutral winds over the mid-latitude ionosonde station Wuhan (30.6° N; 114.4° E) by Lei et al. (2003). Thus, the enhancement of τ at around 45° geomagnetic latitude is clearly visible in Figure 18 for Southern winter night and high solar activity conditions. At mid-latitudes the equatorward direction of meridional thermospheric winds during night exists also in other seasons thus maintaining the ionization level of the ionosphere as seen e.g. in Figure 14 for summer conditions and subsequent global maps that include different seasons at both hemispheres. It is interesting to note that Fang et al. (2018) found enhanced variability of GNSS-derived TEC at around 40–45° geomagnetic latitude in the night at around 5 h Local Time. Enhanced variability of TEC indicates enhanced dynamics as associated with wind induced plasma uplifting. This is assumed here to be responsible for the peaks of τ and hmF2 and plateaus of TEC and NmF2 visible at around 40–45° geomagnetic latitude in Figure 16. Furthermore, enhanced variability has been found by the same authors for winter conditions, which is in principal agreement with our results shown in Figure 14. The global τ map presented in Figure 18, in addition to enhancements around 40–50°, shows a peculiar behavior between about 0 and 90° W at the Southern hemisphere. This obviously indicates a strong sensitivity of τ to the special geomagnetic field structure in the SAA region when comparing the pattern of Figures 15 and 18. So it can be concluded that improvements of slab thickness modelling can be achieved if a realistic structure of the geomagnetic field is considered. It is evident that the current use of the simplifying dipole model flattens the more complicated structures, as is visible in Figure 20.
 |
Fig. 18 Global map of the equivalent slab thickness for Southern winter at night (20–04 LT) and high solar activity conditions. |
 |
Fig. 19 Global map of the peak electron density height hmF2 averaged over all seasons at night (00–04 LT). |
 |
Fig. 20 Global maps of NSTM at 22 LT for days 1 (left) and 181 (right) under low and high solar activity conditions (F10 = 80 and F10 = 160, respectively). |
It should be mentioned again that the peak values of τ around 45° geomagnetic latitude indicating meridional wind induced uplifting of plasma along geomagnetic field lines in winter (as nicely seen in Fig. 18) is also present in summer times as indicated in Figure 14 (top right), but is less pronounced than in winter time.
An all-season plot of nighttime behavior of hmF2 confirms this view and also the assumption of uplifting due to meridional winds, as seen in Figure 19 by the clearly enhanced values of hmF2 around 45° geomagnetic latitude (maps are provided in geographic coordinates). It is worth noticing that the hmF2 map shows also some peculiar pattern as already mentioned in the South Atlantic Anomaly region of the geomagnetic field when comparing with Figures 15 and 18. This fact again indicates that the SAA plays a significant role in modelling studies not only for the equivalent slab thickness but also for other variables like hmF2. In the subsequent section, we will check the response of τ to other anomalies in ionospheric behavior.
6.2 Ionospheric anomalies
In this section we will check the presence of ionospheric anomalies in the observation data and see how well these effects are described by the equivalent slab thickness observation and NSTM data.
Figure 20 presents global maps of NSTM at night (22 LT). The upper panel maps for LSA are very similar to the lower panel maps representing HSA conditions as discussed earlier when analyzing observation data. There is only a gradual difference with respect to LSA and HSA variations of solar radio flux as a proxy for EUV (cf. Fig. 2).
There is a clear indication of enhanced slab thickness values in Northern winter over the American sector (left panel) and similarly in Southern winter over the Asian sector (right panel). Such a particular behavior of the slab thickness over the American sector during Northern winter was the starting point for the discovery of the Nighttime Winter Anomaly (NWA) effect almost 40 years ago by Jakowski et al. (1981).
In this early study the NWA effect is characterized by strongly enhanced slab thickness values in the winter night over Cuba in the American longitude sector. These enhanced equivalent slab thickness values have been interpreted by downward plasma flux from the plasmasphere. The NWA effect was described and explained in more detail in subsequent publications which considered the mirrored situation of the displacement of the geomagnetic and geographic equators the American and Asian sectors where the deviation between both equators maximizes (Förster & Jakowski, 1986, 1988, Jakowski et al., 1986, 1990b, 2015; Natali & Meza, 2013; Jakowski & Förster, 1995). According to this explanation, interhemispheric plasma fluxes from the summer to the winter hemisphere enhance the ionization level in the winter night, causing the NWA effect at low solar activity, or may even cause nighttime enhancements of ionization (Jakowski et al., 1991b). Since downward plasma fluxes from the plasmasphere may significantly increase the equivalent slab thickness, NSTM as shown in Figure 20 is consistent with the NWA mechanism that implies interhemispheric plasma flow from the summer hemisphere. A considerable part of the high plasmaspheric content returns back to the ionosphere at the summer hemisphere in the evening hours, causing strong enhancements of the peak electron density NmF2, thus forming the Mid-latitude summer night anomaly discussed by several authors (e.g. Lin et al., 2010; Thampi et al., 2011). The strong enhancement of NmF2 on the other hand will lead to a reduction of the equivalent slab thickness, because NmF2 is in the denominator of the ratio τ = TEC/NmF2. Indeed, low slab thickness values are seen in the summer hemisphere at the American sector in the Southern hemisphere forming the Weddell Sea Anomaly (WSA, e.g. Horvath & Essex, 2003; He et al., 2009; Chen et al., 2011) as seen at the left panel of Figure 20. This observation and model result is confirmed by global TEC, NmF2 and τ maps at around 4 h LT for December solstices and LSA conditions (F10 < 100) as published by Huang et al. (2016). Whereas TEC and NmF2 are enhanced over the American sector, the equivalent slab thickness shows low values in the WSA region. The analogy is seen in the Northern summer hemisphere over the Asian sector forming the Okhotsk Sea Anomaly (OSA). Both anomalies form the Mid-latitude Summer Nighttime Anomaly (MSNA, Thampi et al., 2011). As first pointed out by Jakowski et al. (2015), MSNA and NWA are closely related via strong ionosphere–plasmasphere coupling and enhanced uplifting of plasma at mid latitudes via thermospheric winds according to equation (18). In summary, the current version of NSTM already reflects fundamental characteristics of these anomalies in the right way.
The plasma uplifting at around 45° should result not only in enhancements of hmF2 and τ but also in enhancements of the topside plasma scale height. Indeed, this has been discussed recently by Jakowski & Hoque (2018) while presenting the first version of the Neustrelitz Plasma Sphere Model NPSM. It has been shown that the scale height of the lower part of the model peaks also at mid-latitudes or shows at least a plateau as demonstrated in Figure 21. This indicates an extension of the plasmaspheric density towards greater altitudes due to plasma uplifting around geomagnetic mid-latitudes in full agreement with the discussion of equivalent slab thickness behavior in this paper. This observation is confirmed by Su et al. (2017) who found enhanced vertical plasma scale heights at around 660 km height in a broad zonal band nearby 40° geomagnetic latitude (peak at 36°) in particular at night during winter solstices. Attempts to explain this enhancement via plasma temperature failed. Since the vertical scale height is derived from electron density profiles, the topside scale height variable includes also transport processes between the ionosphere and plasmasphere. As pointed out in the previous section, plasma uplifting due to thermospheric meridional winds is strongest in winter nights. This could explain also enhanced scale heights in the topside ionosphere.
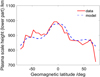 |
Fig. 21 Plasmaspheric scale height HPh derived from observations (red line) and represented by the NPSM (dashed blue line) published by Jakowski & Hoque (2018). Further details concerning observational data and the model can be found in that paper. |
7 Summary and conclusions
For the first time, a global model of the equivalent slab thickness τ (Neustrelitz equivalent Slab Thickness Model – NSTM) over a full solar cycle is presented. The model approach is similar to a family of former model approaches successfully applied for TEC, NmF2 and hmF2 at DLR. The model description focuses on an overall view of the behavior of the equivalent slab thickness as a function of local time, season, geographic/geomagnetic location and solar activity on global scale.
There is a positive correlation of observed and modelled τ with thermospheric temperature variations associated with solar energy input modulated by local time, season and solar activity as expected. Concerning the diurnal variation, this is valid only at daytime, in particular around midday. It is assumed that nighttime plasmasphere–ionosphere coupling causes enhanced equivalent slab thickness values including the pre-sunrise enhancement. This coupling may also cause enhanced scale heights in the topside ionosphere and lower plasmasphere.
Observation data have shown that the behavior of τ is very sensitive to the geomagnetic field structure, both at day- as well as at night-time. The rather simple dipole approximation for the geomagnetic field structure used in the model approach is probably the reason for some inconsistencies which still remain in concrete validation checks. Thus, in particular the SAA region is characterized by extreme high values of the equivalent slab thickness which considerably impact the modelling results and presumably are the reason for some individual misfits. The overall fit provides results consistent with the mid-latitude bulge (MLB) of the equivalent slab thickness, which is described for the first time in this paper. The observation results indicate an effective upward transport of ionospheric plasma at around 45° geomagnetic latitude due to meridional thermospheric winds directed equatorward at night. This effect is clearly seen in the equivalent slab thickness and model data, in hmF2 but also indicated in TEC and NmF2 data. It also agrees quite well with enhanced plasma scale height values in the topside ionosphere found in former plasmasphere modelling studies.
Furthermore, the model recreates quite well ionospheric anomalies such as the Nighttime Winter Anomaly (NWA) which is closely related to the Mid-latitude Summer Night Anomaly (MSNA) such as the Weddell Sea Anomaly (WSA) and Okhotsk Sea Anomaly (OSA).
Deriving either TEC or NmF2 via a slab thickness model from the other two known variables can only be used for rough estimations because of the big variability of the slab thickness and remaining uncertainties. Further model improvements can be achieved by using an extended model approach and considering a more refined geomagnetic field structure.
Acknowledgments
The authors are grateful to the reviewers for their valuable comments. We thank the sponsors and operators of the CHAMP and GRACE missions; Deutsches GeoForschungsZentrum (GFZ) Potsdam, German Aerospace Center (DLR), and the U.S. National Aeronautics and Space Administration (NASA). The authors are also grateful to the sponsors and operators of the FORMOSAT‐3/COSMIC mission; Taiwan’s National Science Council and National Space Organization (NSPO), the U.S. National Science Foundation (NSF), NASA, National Oceanic and Atmospheric Administration (NOAA) and the University Corporation for Atmospheric Research (UCAR) (https://cdaac-www.cosmic.ucar.edu/cdaac/products.html). The authors would like to give thanks to sponsors and operators of NASA’s Earth Science Data Systems and the CDDIS for archiving and distributing the IGS data. The authors would like to acknowledge the support of the University of Bern contributing to the IGS by providing CODE TEC data to the CDDIS for the international science community (https://cddis.nasa.gov/archive/gnss/data/). The authors also thank the Australian Space Weather Agency for publishing ionosonde data via the Australian Government - Bureau of Meteorology, Space Weather Services (ftp://ftp-out.sws.bom.gov.au/data/Geophysical/Historical%20Data/Data%20Files/), as well as the National Geophysical Data Center (NGDC, ftp://ftp.ngdc.noaa.gov/STP/GEOMAGNETIC_DATA/INDICES/KP_AP/) for disseminating historical ionosonde data. This work has been partly funded by the Deutsche Forschungsgemeinschaft (DFG) under the Grant No. HO 6136/1-1 and by the ‘Helmholtz Pilot projects Information & Data Science II’ (Grant support from the Initiative and Networking Fund of the Hermann von Helmholtz-Association Deutscher Forschungszentren e.V. (ZT-I-0022)) with the project named MAchine learning based Plasma density model (MAP). The editor thanks two anonymous reviewers for their assistance in evaluating this paper.
References
- Breed AM, Goodwin GL, Vandenberg AM, Essex EA, Lynn KJW, Silby JH. 1997. Ionospheric total electron content and slab thickness determined in Australia. Radio Sci 32(4): 1635–1643. [CrossRef] [Google Scholar]
- Chen CH, Huba JD, Saito A, Lin CH, Liu JY. 2011. Theoretical study of the ionospheric Weddell Sea Anomaly using SAMI2. J Geophys Res 116: A04305. https://doi.org/10.1029/2010JA015573. [Google Scholar]
- Davies K, Fritz RB, Gray TB. 1976. Measurements of columnar electron contents of the ionosphere and plasmasphere. J Geophys Res 81: 2825–2834. https://doi.org/10.1029/JA081i016p02825. [CrossRef] [Google Scholar]
- Duarte-Silva MH, Muella MTAH, Silva LCC, de Abreu AJ, Fagundes PR. 2015. Ionospheric slab thickness at the equatorial anomaly region after the deep solar minimum of cycle 23/24. Adv Space Res 56(9): 1961–1972. https://doi.org/10.1016/j.asr.2015.05.010. [CrossRef] [Google Scholar]
- Fang TW, Fuller-Rowell T, Yudin V, Matsuo T, Viereck R. 2018. Quantifying the sources of ionosphere day-to-day variability. J Geophys Res: Space Phys 123: 9682–9696. https://doi.org/10.1029/2018JA02552. [CrossRef] [Google Scholar]
- Förster M, Jakowski N. 1986. Interhemispheric ionospheric coupling at the American sector during low solar activity. II. Modelling. Gerl. Beitr Geophys 95(4): 301–314. [Google Scholar]
- Förster M, Jakowski N. 1988. The nighttime winter anomaly (NWA) effect in the American sector as a consequence of interhemispheric coupling. PAGEOPH 127: 447–471. https://doi.org/10.1007/BF00879821. [CrossRef] [Google Scholar]
- Forbes JM, Palo SE, Zhang X. 2000. Variability of the ionosphere. J Atmos Sol-Terr Phys 62(8): 685–693. https://doi.org/10.1016/S1364-6826(00)00029-8. [CrossRef] [Google Scholar]
- Fox MW, Mendillo M, Klobuchar JA. 1991. Ionospheric equivalent slab thickness and its modeling applications. Radio Sci 26(2): 429–438. https://doi.org/10.1029/90RS02624. [CrossRef] [Google Scholar]
- Gerzen T, Jakowski N, Wilken V, Hoque MM. 2013. Reconstruction of F2 layer peak electron density based on operational vertical total electron content maps. Ann Geophys 31: 1241–1249. https://doi.org/10.5194/angeo-31-1241-2013. [CrossRef] [Google Scholar]
- Hajj GA, Romans LJ. 1998. Ionospheric electron density profiles obtained with the global positioning system: Results from the GPS/MET experiment. Radio Sci 33(1): 175–190. https://doi.org/0.1029/97RS03183. [CrossRef] [Google Scholar]
- He M, Liu L, Wan W, Ning B, Zhao B, Wen J, Yue X, Le H. 2009. A study of the Weddell Sea Anomaly observed by FORMOSAT-3/COSMIC. J Geophys Res 114(A1): 2309. https://doi.org/10.1029/2009JA014175. [CrossRef] [Google Scholar]
- Hedin AE, Spencer NW, Biondi MA, Burnside RG, Hernandez G, et al. 1991. Revised global model of thermosphere winds using satellite and ground-based observations. J Geophys Res 96(A5): 7657–7688. https://doi.org/10.1029/91JA00251. [CrossRef] [Google Scholar]
- Hoque MM, Jakowski N. 2011. A new global empirical NmF2 model for operational use in radio systems. Radio Sci 46: RS6015. https://doi.org/10.1029/2011RS004807. [Google Scholar]
- Hoque MM, Jakowski N. 2012. A new global model for the ionospheric F2 peak height for radio wave propagation. Ann Geophys 30: 787–809. https://doi.org/10.5194/angeo-30-797-2012. [CrossRef] [Google Scholar]
- Hoque MM, Jakowski N. 2013. Mitigation of ionospheric mapping function error. In: Proc. of the 26th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2013), September 2013, Nashville, TN, pp. 1848–1855. [Google Scholar]
- Hoque MM, Wenzel D, Jakowski N, Gerzen T, Berdermann J, Wilken V, Kriegel M, Sato H, Borries C, Minkwitz D. 2016. Ionospheric response over Europe during the solar eclipse of March 20, 2015. J Space Weather Space Clim 6: A36. https://doi.org/10.1051/swsc/2016032. [CrossRef] [Google Scholar]
- Horvath I, Essex EA. 2003. The Weddell Sea anomaly observed with the Topex satellite data. J Atmos Sol-Terr Phys 65: 693–706. https://doi.org/10.1016/S1364-6826(03)00083-X. [CrossRef] [Google Scholar]
- Huang Z, Yuan H. 2015. Climatology of the ionospheric slab thickness along the longitude of 120° E in China and its adjacent region during the solar minimum years of 2007–2009. Ann Geophys 33: 1311–1319. https://doi.org/10.5194/angeo-33-1311-2015. [CrossRef] [Google Scholar]
- Huang H, Liu L, Chen Y, Le H, Wan W. 2016. A global picture of ionospheric slab thickness derived from GIM TEC and COSMIC radio occultation observations. J Geophys Res Space Phys 121: 867–880. https://doi.org/10.1002/2015JA021964. [CrossRef] [Google Scholar]
- Jakowski N. 1981. A method for analysing ionospheric perturbations by combining ionospheric total electron content with foF2 data. Phys Solariterr Potsdam 15: 130–136. [Google Scholar]
- Jakowski N, Bettac HD, Lazo B, Lois L. 1981. Seasonal variations of the columnar electron content of the ionosphere observed in Havana from July 1974 to April 1975. J Atmos Sol-Terr Phys 43: 7–11. https://doi.org//10.1016/0021-9169 (81)90003-9. [CrossRef] [Google Scholar]
- Jakowski N, Kugland HG. 1982. Determining the electron content of the plasmasphere using coherent signals of ATS-6 satellite recorded at Neustrelitz. Kosmicheskiye Issledovaniya 6: 892–899. [Google Scholar]
- Jakowski N, Foerster M, Lazo B, Lois L. 1986. Interhemispheric ionospheric coupling at the American sector during low solar activity. I. Observation. Gerl. Beitr Geophys 95(9): 219–227. [Google Scholar]
- Jakowski N, Putz E, Spalla P. 1990a. Ionospheric storm characteristics deduced from satellite radio beacon observations at three European stations. Ann Geophys 8: 343–352. [Google Scholar]
- Jakowski N, Landrock R, Jungstand A. 1990b. The nighttime winter anomaly (NWA) effect at the Asian longitude sector. Gerl Beitr Geophys 99: 163–168. [Google Scholar]
- Jakowski N, Fichtelmann B, Jungstand A. 1991a. Solar activity control of ionospheric and thermospheric processes. J Atmos Terr Phys 53: 1125–1130. https://doi.org/10.1016/0021-9169(91)90061-B. [CrossRef] [Google Scholar]
- Jakowski N, Jungstand A, Lois L, Lazo B. 1991b. Night-time enhancements of the F2-layer ionization over Havana. J Atmos Terr Phys 53: 1131–1138. https://doi.org/10.1016/0021-9169(91)90062-C. [CrossRef] [Google Scholar]
- Jakowski N, Förster M. 1995. About the nature of the night-time winter anomaly effect (NWA) in the F-region of the ionosphere. Planet Space Sci 43: 603–612. https://doi.org/10.1016/0032-0633(94)00115-8. [CrossRef] [Google Scholar]
- Jakowski N, Wehrenpfennig A, Heise S, Reigber C, Lühr H, Grunwaldt L, Meehan TK. 2002. GPS radio occultation measurements of the ionosphere from CHAMP: Early results. Geophys Res Lett 29, 10(10): 95–1–95–4. https://doi.org/10.1029/2001GL014364. [Google Scholar]
- Jakowski N. 2005. Ionospheric GPS radio occultation measurements on board CHAMP. GPS Solut 9: 88. https://doi.org/10.1007/s10291-005-0137-7. [CrossRef] [Google Scholar]
- Jakowski N, Stankov SM, Wilken V, Borries C, Altadill D, et al. 2008. Ionospheric behaviour over Europe during the solar eclipse of 3 October 2005. J Atmos Sol-Terr Phys 70: 836–863. https://doi.org/10.1016/j.jastp.2007.02.016. [CrossRef] [Google Scholar]
- Jakowski N, Hoque MM, Mayer C. 2011a. A new global TEC model for estimating transionospheric radio wave propagation errors. J Geodesy 85: 965–974. https://doi.org/10.1007/s00190-011-0455-1. [CrossRef] [Google Scholar]
- Jakowski N, Hoque MM, Kriegel M, Patidar V. 2015. The persistence of the nighttime winter anomaly (NWA) effect during the low solar activity period 2007–2009. J Geophys Res 120(10): 9148–9160. https://doi.org/10.1002/2015JA021600. [CrossRef] [Google Scholar]
- Jakowski N, Hoque MM, Mielich J, Hall C. 2017. Equivalent slab thickness of the ionosphere over Europe as an indicator of long-term temperature changes in the thermosphere. J Atmos Sol-Terr Phys 163: 91–102. https://doi.org/10.1016/j.jastp.2017.04.008. [CrossRef] [Google Scholar]
- Jakowski N, Hoque MM. 2018. A new electron density model of the plasmasphere for operational applications and services. J Space Weather Space Clim 8: A16. https://doi.org/10.1051/swsc/2018002. [CrossRef] [Google Scholar]
- Jayachandran B, Krishnankutty TN, Gulyaeva TL. 2004. Climatology of ionospheric slab thickness. Ann Geophys 22: 25–33. https://doi.org/10.5194/angeo-22-25-2004. [CrossRef] [Google Scholar]
- Kersley L, Hosseinieh HH. 1976. Dependence of ionospheric slab thickness on geomagnetic activity. J Atmos Sol-Terr Phys 38: 1357–1360. https://doi.org/10.1016/0021-9169(76)90146-X. [CrossRef] [Google Scholar]
- Lei J, Liu L, Luan X, Wan W. 2003. Model study on neutral winds in the ionospheric F- region and comparison with the equivalent winds derived from the Wuhan ionosonde data. TAO 14(1): 1–12. https://doi.org/10.3319/TAO.2003.14.1.1(A). [Google Scholar]
- Lei J, Syndergaard S, Burns AG, Solomon SC, Wang W, et al. 2007. Comparison of COSMIC ionospheric measurements with ground-based observations and model predictions: Preliminary results. J Geophys Res 112: A07308. https://doi.org/10.1029/2006JA012240. [Google Scholar]
- Lin CH, Liu CH, Liu JY, Chen CH, Burns AG, Wang W. 2010. Midlatitude summer nighttime anomaly of the ionospheric electron density observed by FORMOSAT-3/COSMIC. J Geophys Res 115: A03308. https://doi.org/10.1029/2009JA014084. [Google Scholar]
- Maltseva O, Mozhaeva N. 2016a. The use of the total electron content measured by navigation satellites to estimate ionospheric conditions. Int J Navig Obs 2016. https://doi.org/10.1155/2016/7016208. [Google Scholar]
- Maltseva O, Mozhaeva N. 2016b. Efficiency of the equivalent slab thickness of the ionosphere to set radio wave propagation conditions. In: Proc. of the Fifth International Conference on Telecommunications and Remote Sensing, Vol. 1, ICTRS, pp. 5–14. https://doi.org/10.5220/0006226600050014. [Google Scholar]
- McNamara LF, Smith DH. 1982. Total Electron content of the ionosphere at 31 S, 1967–1974. J Atmos Sol-Terr Phys 44(3): 221–239. https://doi.org/10.1016/0021-9169(82)90028-9. [Google Scholar]
- Miro G, Jakowski N, de la Morena BA. 1999. Equivalent slab thickness of the ionosphere in middle latitudes based on TEC/foF2 observations over EL Arenosillo. In: Proc. 3rd COST251 Workshop, September, 1998, Hanbaba R, de la Morena BA (Eds.), pp. 87–92. [Google Scholar]
- Muslim B, Haralambous H, Oikonomou C, Anggarani S. 2015. Evaluation of a global model of ionospheric slab thickness for foF2 estimation during geomagnetic storm. Ann Geophys 58(5): A0551. https://doi.org/10.4401/ag-6721. [Google Scholar]
- Natali MP, Meza A. 2013. The nighttime anomalies using Global IGS VTEC Maps. Adv Space Res 51(3): 377–387. https://doi.org/10.1016/j.asr.2012.09.031. [CrossRef] [Google Scholar]
- Rishbeth H, Mendillo M. 2001. Patterns of F2-layer variability. J Atmos Sol-Terr Phys 63: 1661–1680. https://doi.org/10.1016/S1364-6826(01)00036-0. [CrossRef] [Google Scholar]
- Rüster R. 1971. Solution of the coupled ionospheric continuity equation and the equations of motion for the ions, electrons and neutral particles. J Atmos Sol-Terr Phys 33: 137–14. [CrossRef] [Google Scholar]
- Schaer S, Gurtner W, Feltens J. 1998. IONEX: The IONosphere Map EXchange Format Version 1. In: Proc. of the IGS, AC Workshop, February 9–11, 1998, Darmstadt, Germany. [Google Scholar]
- Schreiner W, Rocken C, Sokolovskiy S, Syndergaard S, Hunt D. 2007. Estimates of the precision of GPS radio occultations from the COSMIC/FORMOSAT-3 mission. Geophys Res Lett 34: L04808. https://doi.org/10.1029/2006GL027557. [CrossRef] [Google Scholar]
- Stankov SM, Jakowski N. 2006. Topside plasma scale height retrieved from radio occultation measurements. Adv Space Res 37: 958–962. https://doi.org/10.1016/j.asr.2005.12.009. [CrossRef] [Google Scholar]
- Su F, Lin J, Zhu F, Zhou Y, Yang J, Hu L. 2017. Seasonal features of topside scale height based on COSMIC measurements. Geod Geodyn 8(5): 328–334. https://doi.org/10.1016/j.geog.2017.06.003. [CrossRef] [Google Scholar]
- Thampi SV, Balan N, Lin C, Liu H, Yamamoto M. 2011. Mid-latitude summer nighttime anomaly (MSNA) – observations and model simulations. Ann Geophys 29: 157–165. https://doi.org/10.5194/angeo-29-157-2011. [CrossRef] [Google Scholar]
- Titheridge JE. 1973. The slab thickness of the mid-latitude ionosphere. Planet Space Sci 21(10): 1775–1793. https://doi.org/10.1016/0032-0633(73)90168-2. [CrossRef] [Google Scholar]
Cite this article as: Jakowski N & Hoque MM 2021. Global equivalent slab thickness model of the Earth’s ionosphere. J. Space Weather Space Clim. 11, 10. https://doi.org/10.1051/swsc/2020083.
All Tables
All Figures
 |
Fig. 1 Overall variation of the equivalent slab thickness as a function of the local time (solid red line) in comparison with model values (dashed blue line). |
| In the text | |
 |
Fig. 2 Equivalent slab thickness as a function of solar activity (F10 index). |
| In the text | |
 |
Fig. 3 Overall variation of the equivalent slab thickness as a function of the season (red line) in comparison with model values (blue line). |
| In the text | |
 |
Fig. 4 Diurnal behavior of the equivalent slab thickness at LSA (F10* < 100) and HSA (120 < F10* < 200) conditions averaged over Northern (NH) and Southern hemispheres (SH). |
| In the text | |
 |
Fig. 5 Daily averaged global maps of observed and modelled τ for LSA (left) and HSA (right) conditions for Northern summer (NS). |
| In the text | |
 |
Fig. 6 Daily averaged global maps of observed and modelled τ for LSA (left) and HSA (right) conditions for Northern winter (NW). |
| In the text | |
 |
Fig. 7 Daytime (08–16 LT) seasonally averaged global maps of observed (upper panels) and modelled τ (lower panels) for LSA (left) and HSA (right) conditions. |
| In the text | |
 |
Fig. 8 Nighttime (20–04 LT) seasonally averaged global maps of observed (upper panels) and modelled τ for LSA and HSA conditions. |
| In the text | |
 |
Fig. 9 Diurnal and seasonal variation of the observed and modelled τ over Tromsø for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
| In the text | |
 |
Fig. 10 Diurnal and seasonal variation of the observed and modelled τ over Juliusruh for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
| In the text | |
 |
Fig. 11 Diurnal and seasonal variation of the observed and modelled τ over Rome for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
| In the text | |
 |
Fig. 12 Diurnal and seasonal variation of the observed and modelled τ over Townsville for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
| In the text | |
 |
Fig. 13 Diurnal and seasonal variation of the observed and modelled τ over Hobart for summer (June/July) and winter (December/January) conditions and for day (6–18 LT) and nighttime (18–6 LT) conditions, respectively. |
| In the text | |
 |
Fig. 14 Variation of the equivalent slab thickness as a function of the geomagnetic latitude (solid red line) in comparison with model values (dashed blue line). Left side: overall data (top) and excluding LSA data (bottom), right side: separated data for summer and winter conditions including both hemispheres. |
| In the text | |
 |
Fig. 15 Effectiveness of vertical plasma transport due to meridional thermospheric winds at 250 km height. |
| In the text | |
 |
Fig. 16 Latitudinal dependences of globally averaged nighttime behavior of equivalent slab thickness, peak electron density NmF2, Peak height hmF2 and vertical total electron content VTEC during winter time, averaged over both hemispheres (time interval: 20–04 LT, years 2001–2018). The equivalent slab thickness observations are compared with corresponding model values (top left, dashed blue line). |
| In the text | |
 |
Fig. 17 Thermospheric winds at mid-latitudes in winter (taken from Hedin et al., 1991). The solid and dashed lines correspond to wind models HWM90 and HWM87, respectively. The different numbers refer to different observation techniques. For further details see Hedin et al. (1991). |
| In the text | |
 |
Fig. 18 Global map of the equivalent slab thickness for Southern winter at night (20–04 LT) and high solar activity conditions. |
| In the text | |
 |
Fig. 19 Global map of the peak electron density height hmF2 averaged over all seasons at night (00–04 LT). |
| In the text | |
 |
Fig. 20 Global maps of NSTM at 22 LT for days 1 (left) and 181 (right) under low and high solar activity conditions (F10 = 80 and F10 = 160, respectively). |
| In the text | |
 |
Fig. 21 Plasmaspheric scale height HPh derived from observations (red line) and represented by the NPSM (dashed blue line) published by Jakowski & Hoque (2018). Further details concerning observational data and the model can be found in that paper. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.