| Issue |
J. Space Weather Space Clim.
Volume 5, 2015
|
|
|---|---|---|
| Article Number | A6 | |
| Number of page(s) | 5 | |
| DOI | https://doi.org/10.1051/swsc/2015007 | |
| Published online | 27 February 2015 | |
Research Article
Atmospheric effect corrections of MuSTAnG data
1
Institute of Physics, Ernst-Moritz-Arndt University of Greifswald, Felix-Hausdorff-Str. 6, 17487
Greifswald, Germany
2
Yerevan Physics Institute, Alikhanian Brothers Str. 2, 0036
Yerevan, Armenia
3
Present address: Forschungszentrum Jülich GmbH, Jülich Centre for Neutron Science (JCNS), Outstation at MLZ, Lichtenbergstrasse 1, 85747
Garching, Germany
4
Pushkov Institute of Terrestrial Magnetism, Ionosphere and Radio Wave Propagation (IZMIRAN), Kalushskoe ave. 4, 142190
Troitsk, Moscow, Russia
* Corresponding author: mary@yerphi.am
Received:
15
May
2014
Accepted:
24
January
2015
The atmospheric effect correction of the muon flux measured by ground level telescopes is of special importance for further study of cosmic ray variations. The Duperier method is used to correct atmospheric effects on the muon intensity observed by the MuSTAnG telescope. Linear multiple correlation and regression analysis are applied to the data registered during the year 2009. The aerological data are obtained from daily radiosonde balloon flights of Deutscher Wetterdienst. The regression coefficients and total correlation coefficients are calculated for all directional channels. The seasonal variations are eliminated from the MuSTAnG telescope data. The results are compared with theoretical elimination of temperature variations.
Key words: Space weather / muon telescope / atmospheric effect
© M. Zazyan et al., Published by EDP Sciences 2015
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1. Introduction
The Muon Space Weather Telescope for Anisotropies (MuSTAnG) (Jansen et al. 2001; Hippler et al. 2008) is presently operating at Greifswald University in Germany to study variations in cosmic rays muon flux. The count rate variation in such instruments is used to study a variety of solar and heliospheric phenomena. However, the wide use of muon detectors for the research of cosmic rays variations is restrained by the presence of atmospheric effects inherent to the muon component of CR.
The investigation of atmospheric effects is of special importance for the further study of cosmic ray variations, since only after the correction for such effects can the measured data provide information on the variations due to causes beyond the Earth’s atmosphere.
The two main causes of variations in the cosmic ray flux originating from the Earth’s atmosphere are the barometric effect and the temperature effect (Dorman 1974). The barometric effect is determined by only a single parameter, namely the pressure at the detection level. Pressure correction procedures are well established for surface detectors world-wide (Dorman 2004). However, muon observations require additional corrections for the positive and negative temperature effect. Atmospheric temperature effect corrections are correspondingly more complicated. The temperature effect is generally determined by the overall profile of the atmosphere from the level of origin to the detection level, and hence is more difficult to interpret. To exclude the temperature effect, aerologic sounding data near the detector location are necessary. More often such data are missing and it is impossible to restore them in retrospective, or the soundings aren’t carried out regularly. Fortunately, there is a weather station in Greifswald (Deutscher Wetterdienst) which routinely takes upper air observations by releasing sounding balloons twice a day at 12:00 and at 24:00 (CEST). These aerological data obtained from the daily radiosonde balloon flights can be used to correct the muon flux measured by the MuSTAnG telescope.
2. Method
Usually, the temperature correction procedure is applied after elimination of the pressure effect. There exist different methods (empirical and theoretical) to correct cosmic ray data for atmospheric temperature effects: the method of effective level of generation (Duperier 1949), the integral method (Olbert 1953; Maeda & Wada 1954; Dorman 1964), the method of effective temperature (Barrett et al. 1952), the method of mass-average temperature (Dvornikov et al. 1976). All these methods depend on the observation of temperature at different altitudes. But we also can get the temperature profile data from global meteorological models, for example the GFS (Global Forecast System, http://www.nco.ncep.noaa.gov/pmb/products/gfs/) model developed by the National Centers for Environmental Prediction – NCEP (USA). The GFS model’s data were used in the temperature effect analysis for the MuSTAnG telescope in previous work (Ganeva et al. 2013). The use of this data allows us to calculate the temperature effect in real time (Berkova et al. 2012).
In this work we will consider corrections according to the Duperier method. It should be noticed that the method used in our work allows exclusion of pressure and temperature effect simultaneously, combining pressure, positive temperature and height effects on the muon intensity. Our results will be compared with the results of Ganeva et al. (2013) based on meteorological models.
The Duperier method or the method of effective level of generation is based on the assumption that muons are generated around the isobaric level 100 mb. The height of this pressure level in the atmosphere varies, particularly seasonally. The transit time through the atmosphere of muons will be longer when this pressure level is located at a higher altitude and more muons will decay before reaching a detector. The increase in height of this level arises from an expansion of the atmosphere when it is warmer and so this effect is known as the negative temperature effect. When the temperature near the pion production level is higher the air density is lower and the likelihood of the pion interacting before it decays into a muon is reduced resulting in higher count rates. This is known as the positive temperature effect (Duldig 2000). At the energies recorded by the ground level detectors (tens of GeV) the negative temperature effect dominates, and at underground registration (>100 GeV) the positive temperature effect prevails.
The method of effective level of generation is the simplest methodology of temperature correction and is still useful for properly correcting the temperature effect on a yearly perspective.
Duperier has presented a linear regression equation for the intensity registered on ground during the quiet sun (1)
(1)
The equation for relative variations is then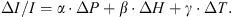 (2)
(2)
Here, α is the partial pressure coefficient (%/hPa), β is the height coefficient (%/km) and γ is the positive temperature coefficient (%/C). P is the ground pressure and H and T are the height and the temperature of the reference layer (the level of maximum muon production). ∆P is the deviation of the pressure, ∆H and ∆T are the deviations of the height and the temperature of the reference layer, and ∆I is the deviation of the muon count rate from their annual averages, respectively.
Generally the temperature effect of the cosmic ray intensity is characterized by one or two terms in Eq. (2) (Braga et al. 2013; Okazaki et al. 2008; Sagisaka 1986):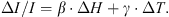 (3)
(3)
The full formula is used to simultaneously eliminate pressure, positive temperature and height effects on the muon intensity (Baker et al. 1993).
Having determined a set of corrections coefficients the intensity corrected for atmospheric effects becomes (as function of time):![$$ {I}_{\mathrm{corr}}=\enspace I(t)/([1+\alpha (P(t)-{P}_0)+\beta (H(t)-{H}_0)+\gamma (T(t)-{T}_0)]). $$](/articles/swsc/full_html/2015/01/swsc140023/swsc140023-eq4.gif) (4)
(4)
Here, P0, H0 and T0 are the annual averages of the ground pressure, the height and the temperature of the reference layer, respectively.
3. Analysis
We have applied a linear multiple correlation and regression analysis to the data registered by the MuSTAnG telescope during 2009. The year 2009 was chosen due to the minimum of solar activity. The aerological data were obtained from daily radiosonde balloon flights (Deutscher Wetterdienst, Weather station Greifswald). As a reference layer the pressure level of 100 hPa was used.
Figure 1 shows the variations of the air temperature at the 100 hPa level (a), height of the 100 hPa level (b), ground pressure (c) and muon relative intensity detected by the vertical channel of the MuSTAnG telescope (d). One can see a clear anti-correlation between the variations in muon rates and the height of the 100 hPa level (negative temperature effect), which predominates typically at ground-based detectors.
 |
Fig. 1. Variations of the temperature at the 100 hPa level (a); the height of the 100 hPa level (b); the ground pressure (c); muon relative intensity (d) during 2009. |
We have computed the correlation matrix which represents the correlation between all pairs of variables. The correlation matrix for the vertical direction is presented in Table 1. This table clearly demonstrates that there is a strong anti-correlation between the variations in muon rates and the height of the 100 hPa level and no significant correlation with the temperature of the 100 hPa level. As can be seen from Table 1, muon rates also show strong anti-correlation with pressure.
Correlation coefficients between all pairs of variables for the vertical direction of the MuSTAnG telescope.
4. Results and discussion
The regression coefficients and the total correlation coefficient R calculated for all directional channels are presented in Table 2. One can see that the variation in the pressure coefficients between channels is not significant while the variations in the temperature/height effects seem significant. Since the muon energy does not vary significantly over channels (Hippler & Zazyan 2012), changes in β and γ are not related to the muon energy. Determination of the coefficients strongly depends on the accuracy of the data. The ground level pressure is measured quite accurately, while height and temperature of the 100 hPa level may bear large measurement errors. Apparently, the errors in the measured parameters lead to the observed variations of β and γ.
The regression coefficients (α, β and γ) and the total correlation coefficient (R) calculated for all directional channels of the MuSTAnG telescope.
After applying the atmospheric corrections by using the calculated coefficients, the seasonal variation can be eliminated. The results for the vertical direction are shown in Figure 2. The muon intensity I in counts per hour during 2009 is plotted. Comparing the pressure corrected data with the pressure and temperature corrected data, one can see that only the latter one allows us to eliminate seasonal variations.
 |
Fig. 2. The muon intensity detected by the vertical channel of the MuSTAnG telescope. |
In Figure 3 we compare our results for the year 2009 (vertical direction) with that of Ganeva et al. (2013), where the effective temperature method is used.
 |
Fig. 3. The muon intensity detected by the vertical channel of the MuSTAnG telescope corrected using the Duperier method with sounding data and the effective temperature method with the GFS model for the temperature calculation. |
According to this method correlation between temperature and muon intensity can be described by the effective temperature Teff, in which the contributions of all atmosphere levels are accounted for with the proper weights. The relationship between atmospheric temperature fluctuations and muon intensity variations is ∆Ι/I0 = αT ∆Teff/Teff. Details can be found in Barrett et al. (1952). In Ganeva et al. (2013) vertical temperature atmospheric profiles obtained from NCEP’s Global Forecast System (GFS) temperature model were used.
To compare results obtained by both of the methods, the experimental temperature measured at the weather station in Greifswald was interpolated by a cubic spline function to obtain hourly data.
Figure 3 shows that both methods result in nearly the same residual fluctuation of the corrected muon rates. Size of the time bin is always one hour. The time of atmospheric measurement is always the start of the muon bin.
5. Conclusions
In this work the Duperier method was used to correct for atmospheric effects on the muon intensity observed by the MuSTAnG telescope. The correction coefficients were determined for the base period of the year 2009. The correction of muon intensities was carried out for all directional channels of the MuSTAnG telescope. Corrected muon rates were compared to the results for the elimination of temperature variations obtained by the effective temperature method. It is shown that the Duperier method with three atmospheric variables leads to essentially the same atmospheric corrections of the MuSTAnG telescope intensity as the more complicated effective temperature method applied in Ganeva et al. (2013).
Acknowledgments
Construction of MuSTAnG was supported by the European Space Agency (ESA) and by the Deutsches Zentrum für Luft- und Raumfahrt (DLR).
M. Zazyan thanks The German Academic Exchange Service (DAAD) for providing the opportunity for a research stay at the University of Greifswald.
The editor thanks T. Catanach and an anonymous referee for their assistance in evaluating this paper.
References
- Baker, C.P., D.L. Hall, J.E. Humble, and M.L. Duldig. Atmospheric correction analysis for the Mawson muon telescopes. Proc. of 23th International Cosmic Ray Conference, Calgary, 3, p. 753, 1993. [Google Scholar]
- Barrett, P., et al. Interpretation of cosmic-ray measurements for underground. Rev. Mod. Phys., 24, 133, 1952. [CrossRef] [Google Scholar]
- Berkova, M., A. Belov, E. Eroshenko, and V. Yanke. Temperature effect of muon component and practical questions of how to take into account in real time. Astrophys. Space Sci. Trans., 8, 41–44, 2012, http://www.astrophys-space-sci-trans.net/8/41/2012/astra-8-41-2012.pdf. [CrossRef] [Google Scholar]
- Braga, C.R., A. Dal Lago, T. Kuwabara, N.J. Schuch, and K. Munakata. Temperature effect correction for the cosmic ray muon data observed at the Brazilian Southern Space Observatory in São Martinho da Serra. J. Phys.: Conf. Ser., 409, 012138, 2013. [CrossRef] [Google Scholar]
- Dorman, L.I. On the temperature effect of the hard component of cosmic rays. Dokl. Akad. Sci. Nauk SSSR, 95, 49, 1964. [Google Scholar]
- Dorman, L.I. Cosmic rays. Variations and space explorations, North-Holland, Amsterdam, 1974. [Google Scholar]
- Dorman, L.I. Cosmic rays in the Earth’s atmosphere and underground, Kluwer Academic Publishers, USA, 2004. [CrossRef] [Google Scholar]
- Duldig, M.L. Muon observations. Space Sci. Rev., 93, 207–226, 2000. [CrossRef] [Google Scholar]
- Duperier, A. The meson intensity at the surface of the Earth and the temperature at the production level. Proc. Phys. Soc., 62A, 684–696, 1949. [CrossRef] [Google Scholar]
- Dvornikov, V.M., Yu.Ya. Krestyannikov, and A.V. Sergeev. Determination of the mass-average temperature on the cosmic ray intensity data. Geomag. Aeron., 16 (5), 923–925, 1976. [Google Scholar]
- Ganeva, M., S. Peglow, R. Hippler, M. Berkova, and V. Yanke. Seasonal variations of the muon flux seen by muon telescope MuSTAnG. J. Phys.: Conf. Ser., 409, 012242, 2013, DOI: 10.1088/1742-6596/409/1/012242. [CrossRef] [Google Scholar]
- Hippler, R., A. Mengel, F. Jansen, G. Bartling, W. Göhler, et al. First space weather observations at MuSTAnG – the muon space weather telescope for anisotropies at Greifswald. Proc. of 30th International Cosmic Ray Conference, Mexico, 1, pp. 347–350, 2008. [Google Scholar]
- Hippler, R., and M. Zazyan. Simulation of MuSTAnG telescope response to cosmic rays. Proc. Cosmic Ray Summer School, Nor-Amberd International Conference Center, p. 30, 2012. [Google Scholar]
- Jansen, F., K. Munakata, M.L. Duldig, and R. Hippler. Muon detectors – the real-time, ground based forecast of geomagnetic storms in Europe. ESA Space Weather Workshop: Looking towards a European Space Weather Programme, 2001, ESA WPP-144. [Google Scholar]
- Maeda, K., and M. Wada. Atmospheric temperature effect upon the cosmic ray intensity at sea level. J. Sci. Res. Inst., Tokyo, 48, 71–79, 1954. [Google Scholar]
- Olbert, S. Atmospheric effects on cosmic ray intensity near sea level. Phys. Rev., 92, 454, 1953. [CrossRef] [Google Scholar]
- Okazaki, Y., A. Fushishita, T. Narumi, C. Kato, S. Yasue, et al. Drift effects and the cosmic ray density gradient in a solar rotation period: First observation with the Global Muon Detector Network (GMDN). Astrophys. J., 681, 693–707, 2008. [CrossRef] [Google Scholar]
- Sagisaka, S. Atmospheric effects on cosmic-ray muon intensities at deep underground depths. Nuovo Cimento C, 9, 809, 1986. [Google Scholar]
Cite this article as: Zazyan, M., M. Ganeva, M. Berkova, V. Yanke & R. Hippler. Atmospheric effect corrections of MuSTAnG data. J. Space Weather Space Clim., 5, A6, 2015, DOI: 10.1051/swsc/2015007.
All Tables
Correlation coefficients between all pairs of variables for the vertical direction of the MuSTAnG telescope.
The regression coefficients (α, β and γ) and the total correlation coefficient (R) calculated for all directional channels of the MuSTAnG telescope.
All Figures
 |
Fig. 1. Variations of the temperature at the 100 hPa level (a); the height of the 100 hPa level (b); the ground pressure (c); muon relative intensity (d) during 2009. |
| In the text | |
 |
Fig. 2. The muon intensity detected by the vertical channel of the MuSTAnG telescope. |
| In the text | |
 |
Fig. 3. The muon intensity detected by the vertical channel of the MuSTAnG telescope corrected using the Duperier method with sounding data and the effective temperature method with the GFS model for the temperature calculation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


