| Issue |
J. Space Weather Space Clim.
Volume 10, 2020
|
|
|---|---|---|
| Article Number | 21 | |
| Number of page(s) | 15 | |
| DOI | https://doi.org/10.1051/swsc/2020017 | |
| Published online | 09 June 2020 | |
Research Article
Comparisons of spectrally resolved nightglow emission locally simulated with space and ground level observations
1
DOTA, ONERA, 91761 Palaiseau, France
2
School of Geosciences, University of Edinburgh, Crew Building, The King’s Buildings, EH9 3FF Edinburgh, UK
3
LATMOS-IPSL, CNRS/INSU, UMR 8190, Université de Versailles Saint-Quentin-en-Yvelines, 78280 Guyancourt, France
* Corresponding author: pierre.simoneau@onera.fr
Received:
19
December
2018
Accepted:
16
March
2020
A mesospheric model of the airglow emission is developed to recover the night variations observed at ground level. The model is based on a 1D vertical photochemical model, including the photodissociation and heating processes. The spectral radiation is calculated at high altitude and propagated through the atmosphere to the ground. We also include short scale vertical dynamic such as turbulences and the molecular diffusion. Simulations reveal realistic emissions when compared with space observations. In addition, we estimate the impact of changes associated with parameterized atmospheric tides. The comparison with observations is performed over high altitude and ground level. We confront the model outputs at high altitude with satellite observations (SABER and GOMOS) and the simulations propagated at ground level are compared to local measurements campaigns performed in France and India. Biases between observed and simulated radiances and volume emission rates are suspected to be due to the impact of gravity waves or the large scale dynamic.
Key words: Nightglow emission / modeling / mesosphere
© C. Bellisario et al., Published by EDP Sciences 2020
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The night airglow is the radiation emitted over a wide spectrum originating from the chemical de-excitation of molecules in the mesosphere and thermosphere. Discovered by Meinel (1950), it has been studied for decades. First investigations were made by ground-based observations (Chamberlain & Roesler, 1955) and rocket measurements (Baker & Stair, 1988). Satellites allowed direct observation of the nightglow outside the atmosphere with a large spatial and temporal coverage. Among them, WINDII (Shepherd et al., 2012), SABER (Marsh et al., 2006), HRDI (Burrage et al., 1994) or more recently GOMOS (Bellisario et al., 2014) built the main climatology of the various sources of the nightglow.
The main feature of the emission comes from the infrared emission of the rovibrationally excited OH (Leinert et al., 1997) created by the reaction of H and O3. Many factors have an effect on the variations of the signal. For example, gravity waves increase locally the intensity of the emission, tides induces diurnal variations, atomic oxygen controls the ozone recombination and therefore the airglow intensity. The observation of the emission can then be a useful signature for the understanding of the various physical and chemical phenomena occurring at high altitude such as the role of the gravity waves (Hines, 1960) and atmospheric tides (Petitdidier & Teitelbaum, 1977).
Both imaging systems and spectrometers enable the observation of the airglow. The first ones, with a large field of view, measure the photon quantity emitted by the airglow layer (Takahashi & Batista, 1981; Lowe et al., 1991), and retrieve the structures at high altitude such as gravity waves (Taylor et al., 1995a, 1995b; Pautet et al., 2014) and tides (Mulligan & Nallen, 1998). The second ones allow the studies of the rovibrational population of OH, the retrieval of temperature (Takahashi & Batista, 1981), and the wind velocity (Didebulidze et al., 2011).
Many studies used an analytical approach for the estimation of the airglow emission. For example, Le Texier et al. (1987) use a two-dimensional dynamical and photochemical coupled numerical model to estimate the annual variations of the OH emission layer for various latitudes. McDade (1991) investigates vertical variations of the OH vibrational distributions, in particular the impact of quenching and vibrational deactivation processes. Altitude of the OH nightglow layer is also predicted by Liu & Shepherd (2006) using a multiple linear regression analysis of six years of WINDII records. Relations between gravity waves and O2 and OH airglows perturbations are highlighted by Liu & Swenson (2003) with the help of a one-dimensional model. Grygalashvyly et al. (2014) show the mean state and trends of the hydroxyl layer during the period 1961–2009 by coupling an OH*-model with a chemistry-transport model.
However, these studies do not spectrally resolve the emission as they only produce global – or transition specific – volume emission rate (VER). In order to simulate the emission spectrum at the various altitudes concerned, it is mandatory to include in the model the various excited states implicated in the emission as reactive species. Very few models able to simulate the full spectrum observed at high altitude were developed and none are available for ground-based analyses. Moreels et al. (1977) describe a 1D chemical model with eddy diffusion but without dynamical effects or heating and suffers from instability. Rodrigo et al. (1991) also include O(1D) and O2(1∆) to discuss the Eddy diffusion coefficient. Makhlouf et al. (1995) look at the atomic oxygen green line at 557.7 nm and OH emission in a diurnal 1D model which pairs up with a simple gravity wave model to study their perturbations (Makhlouf et al., 1998). Yee et al. (1997) model is based on TIME, implemented with OH, O2 and O emission reactions and comparisons with satellite observations from HRDI. More recently, Fytterer et al. (2019) derive night-time atomic oxygen and atomic hydrogen in the mesopause region by extending a chemistry box model with several chemical reactions and physical quenching processes involving OH(ν), providing in addition transitional VER. It is worth noting that these models listed above are not implemented with a radiative transfer model, required in order to propagate the spectrum simulated at high altitude down to the ground.
The objective of this study consists in simulating nightglow that can be observed at ground level. Therefore a local photochemical model was developed based on the most up-to-date coefficients. On the contrary to other models, various excited states along with a radiative transfer module are included in order to obtain the OH spectral emission emitted at high altitude, and propagate it down to the ground through interaction with the neutral atmosphere for comparison to local measurements. To include the various dynamical processes on the 1D model, temperature and wind fluctuations over short timescales are forced and simulated externally.
Interests of such a study are manifold. Right below the boundary between Earth’s atmosphere and outer space, the knowledge of the energy exchange such as gravity waves breaking are important to better constrain climate models. Temperature, wind velocity, or molecule concentrations are variables that can be retrieved with the observation of the airglow (Khomich et al., 2008). Seen from the ground, the airglow layer is also important. In the case of infrared astronomy, H band included between 1.45 μm and 1.8 μm is polluted by OH emission. A flat field is commonly used to estimate this pollution over integration time of few hours, not taking into account its short time variability. Other spectral bands can also be impacted (Slanger et al., 2003). Finally, passive night vision system are interested in using the airglow emission layer propagated down to the ground and reflected by the surface (Derelle et al., 2012).
In the following section, we describe the various parts of the model, including the photodissociation processes, the heating, the emission calculation and propagation. Local dynamic in 1D is implemented and a tide parameterization is used. Then we present the first results of the model and a short sensitivity test on the tidal effects. Finally, we compare the outputs of the model at high altitude with observations from space using SABER instrument and GOMOS spectrometer, and ground-based IR camera obtained during successive measurement campaigns to test the model output and suggest the next steps required to improve the model.
2 Description of the model
2.1 The photochemical code
Since we aim to build a model simulating the photochemical reactions at high altitude, 24 species are taken into account in the model (Table 1), including the calculation of all the vibrational states of OH and excited states of molecular and atomic oxygen. The stable species are used as inputs producing as outputs the excited states listed in Table 1, distributed on a vertical 1D grid. Then, these excited species lead to the computation of atmospheric spectral emission or integrated VER (see Sect. 2.4). Table A.1 lists the chemical reactions used in the model, following the numbering from Moreels et al. (1977). Eighty one reactions are taken into account and the reaction coefficients are mostly taken from the JPL atmospheric data (Sander et al., 2011). We use the backward Euler method based on the Taylor series to resolve the chemical system Jacobson (2005). This method brings a positive solution regardless the selected time step and the solution is also iterated in order to insure the stability and precision of the system.
List of the species used in the present model. Excited states are used for OH (all vibrational, from 1 to 9), and also O2(1∆), O2(1Σ), O(1D), and O(1S).
Initial data originate from MSISE-90 data (Hedin, 1991) for local comparison. MSISE-90 model intends to provide the neutral temperature and densities (e.g., O, N2, O2, and H) up to thermospheric heights. For other cases, standard atmospheric profiles are interpolated over a vertical grid ranging from 25 km to 125 km with a 500 m altitude resolution. Chemistry of NOx, ClOx, and COx have been left out to alleviate the system since their contributions are mostly prominent below 25 km (Brasseur & Solomon, 2005).
2.2 Chemical photodissociation
The OH vibrational states originate from the reaction (8) between H and O3 (Table A.1). As the ozone photodissociates during the day, the model runs starting from the previous night to reproduce a realistic ozone profile. In order to compute photodissociation effects, we use a combination of high resolution SOLSPEC solar spectrum (Thuillier et al., 2009) and SOLSTICE experiment for UV range (Rottman et al., 2001) based on SUSIM instrument (Floyd et al., 2002). Interpolations have been operated down to 0.05 nm in the UV region to take into account the Lyman-α line, the Schumann–Runge and the Huggins bands. Above 3 μm, data are derived from Thekaekara (1974). The solar zenith angle is calculated using the Chapman function (Smith & Smith, 1972) to estimate the optical depth. The solar irradiance is propagated through the Beer–Lambert law at each altitude level. The induced photolysis acts on several molecules: O2, O3, H2O, H2O2 and HO2. Cross sections of the molecules are taken from the Max-Planck Institute to Harvard CfA. For the Rayleigh diffusion, we use Nicolet’s formula (Nicolet, 1984). Since the cross sections of O2 and O3 display large variations in some spectral band, a fine resolution of 10−4 μm is used to simulate the spectral details in the Schumann–Runge band, the Chappuis band and around the Lyman-α wavelength. The spectral quantum yields for the produced species are summarized on Tables A.2 and A.3 and are taken from Moreels et al. (1977). For the visible and IR region, the resolution is from 10−2 μm up to 1 μm in order to avoid long computation time.
2.3 Heating effects
The mesopause is subject to strong energy exchanges (Mlynczak, 1997). The importance of the heating has been noticed by Mlynczak (2000). We consider in the model the solar heating, the chemical heating, and also the radiation cooling (by CO2). The solar irradiance is absorbed by the O2 and O3 molecules between 50 km and 110 km (Brasseur & Solomon, 2005). The energy is enough to break the chemical bounds of the molecules. The difference of energy between the initial and final states is converted into kinetic energy. We apply here the formulation from Brasseur & Solomon (2005) that expresses the difference of absorbed solar radiation at a specific layer i, between two vertical levels: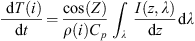 (1)with dT/dt the heating rate, i.e. the variation of the temperature T with time t at the layer i, the solar zenith angle Z, the density ρ, the calorific capacity CP, and I(z, λ) the incident solar intensity at a wavelength λ and an altitude z. The formulation is valid for middle atmosphere, in the absence of clouds. The correction of CP with the range of temperature is assumed to be small and therefore neglected. This leads to heating up to 10 Kelvins per day.
(1)with dT/dt the heating rate, i.e. the variation of the temperature T with time t at the layer i, the solar zenith angle Z, the density ρ, the calorific capacity CP, and I(z, λ) the incident solar intensity at a wavelength λ and an altitude z. The formulation is valid for middle atmosphere, in the absence of clouds. The correction of CP with the range of temperature is assumed to be small and therefore neglected. This leads to heating up to 10 Kelvins per day.
Exothermic reactions in the middle atmosphere have been listed by Mlynczak & Solomon (1993) (Tables A.5). We apply their formulation for the calculation of the temperature variation induced by the exothermic reactions: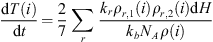 (2)with kr the rate of the considered reaction, the density of the reactants considered ρ(1, 2) and air ρ, the reaction enthalpy H, the Boltzmann constant kb and the Avogadro number NA.
(2)with kr the rate of the considered reaction, the density of the reactants considered ρ(1, 2) and air ρ, the reaction enthalpy H, the Boltzmann constant kb and the Avogadro number NA.
The radiative cooling tallies with the CO2 infrared radiation around 15 μm. We use here the Fomichev parametrisation (Fomichev et al., 1998) which takes into account local thermodynamic equilibrium (LTE) and non-LTE effect at high altitude.
These heating rates, encompassing the solar heating, the chemical heating and the radiative cooling are multiplied by the time step of the model, providing a temperature perturbation within the layer. The profiles of the different heating rate profiles show that, in the stratosphere, chemical heating, and radiative cooling have a similar amplitude. Around the mesopause, the chemical heating exhibits the strongest effect. At higher altitude, the solar heating gets more important together with the radiative cooling.
2.4 Emission calculation
Since we aim to compare the model results with ground based observations, we compute the fully resolved spectrum of the airglow. The intensity of an emission line is written according to: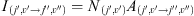 (3)where I(j′,ν′→j″,ν″) is the transition intensity between the rovibrational state (j′, ν′) and (j″, ν″), j and ν are respectively the rotational and vibrational quantum numbers, N(j′,ν′) is the population of the rovibrational state, and A(j′,ν′→j″,ν″) is the Einstein coefficient of the transition taken from Turnbull & Lowe (1989) (see Tables A.2 and A.4). The photochemical part of the model calculates the populations of the various vibrational excited states of OH. And then, the rotational population of each vibrational state is computed using the Boltzmann distribution.
(3)where I(j′,ν′→j″,ν″) is the transition intensity between the rovibrational state (j′, ν′) and (j″, ν″), j and ν are respectively the rotational and vibrational quantum numbers, N(j′,ν′) is the population of the rovibrational state, and A(j′,ν′→j″,ν″) is the Einstein coefficient of the transition taken from Turnbull & Lowe (1989) (see Tables A.2 and A.4). The photochemical part of the model calculates the populations of the various vibrational excited states of OH. And then, the rotational population of each vibrational state is computed using the Boltzmann distribution.
At this stage, it is also possible to compute the VER ϵ based on the vibrational excited states of [OH]ν and the Einstein coefficients Aν from Turnbull & Lowe (1989). The VER for a specific vibrational transition is given by:![$$ \epsilon =\frac{{[\mathrm{OH}]}_v}{{A}_v}. $$](/articles/swsc/full_html/2020/01/swsc180077/swsc180077-eq4.gif) (4)
(4)
It is also worthily to mention that because of the low temperature at this altitude, the local thermal emission of the atmosphere is spectrally located in the mid and far infrared and does not interfere with the emission.
2.5 Emission propagation
The emission propagation is insured by the model RAYJN developed by ONERA (Simoneau et al., 2011). It calculates the radiation at the ground including the solar radiation (in daily conditions), the thermal radiation of the atmosphere and the nightglow emission. The diffusion through the atmospheric layers follows the discrete-ordinate method developed by Nakajima & Tanaka (1986). The radiative transfer equation is written hereafter: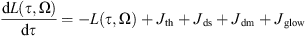 (5)with L(τ, Ω), the radiance for the optical depth τ, which propagates in the direction Ω. Jth, Jds, Jdm, and Jglow are the different sources functions, respectively from the thermal emission, the simple scattering, the multiple scattering and the nightglow emission. The expressions of the various sources follow:
(5)with L(τ, Ω), the radiance for the optical depth τ, which propagates in the direction Ω. Jth, Jds, Jdm, and Jglow are the different sources functions, respectively from the thermal emission, the simple scattering, the multiple scattering and the nightglow emission. The expressions of the various sources follow: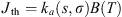 (6)
(6)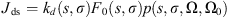 (7)
(7)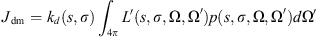 (8)
(8)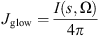 (9)with s denoting the position, σ the wavenumber, B(T) the Planck function, ka and kd the absorption and diffusion coefficient, F0 the solar radiance, p the phase function associated to the angle (ɷ, ɷ′), L the radiance, I the intensity of the nightglow emission. An example of the spectrum modeled at high altitude (in red) and the result at the ground level (in black) is given in Figure 1. We observe the strong absorption band around 1.4 μm originating from the water vapor absorption.
(9)with s denoting the position, σ the wavenumber, B(T) the Planck function, ka and kd the absorption and diffusion coefficient, F0 the solar radiance, p the phase function associated to the angle (ɷ, ɷ′), L the radiance, I the intensity of the nightglow emission. An example of the spectrum modeled at high altitude (in red) and the result at the ground level (in black) is given in Figure 1. We observe the strong absorption band around 1.4 μm originating from the water vapor absorption.
 |
Fig. 1 Example of a spectrum at 87 km (in red) and the same spectrum propagated at the ground level (in black). We notice the strong water vapor absorption band around 1.4 μm. |
2.6 Vertical dynamic
Local vertical dynamic responsible for the chemical components transport is induced by the Eddy diffusion, the molecular diffusion, and the wind advection. The turbulence (Eddy) diffusion starts with the Eddy diffusion coefficient, calculated with the formula from Lindzen (1981). At the same time, the diffusion coefficient is calculated with the formula from Jacobson (2005). We verify that turbulences are prevailing below 100 km and then diffusion overtakes the vertical dynamic. We use the Crank–Nicolson forward implicit Euler Scheme, which is in second order in time to resolve the turbulence-diffusion equation.
The wind advection presents two components, the vertical drift velocity, calculated with the molecular diffusion coefficient, and the tidal wind, which is described in the next paragraph. We use here a semi-Lagrangian scheme to resolve the advection.
The dynamic dominates long-lived species loss rates. For example, O(1D) is driven by the dynamic up to 90 km. Above, the emission dominates the loss rate. On the other side, the excited states of OH are short-lived and therefore the emission dominates the loss rates. Nonetheless, because of the dependance of the OH excited states on the concentration of species such as O3, the dynamic remains important to properly simulate the emission rates.
2.7 Tides parameterization
To ensure a fair representation of the migrating tides in the timescale of a night, we use simulations performed by the Global-Scale Wave Model (GSWM) (Hagan et al., 1999). It solves the linearized Navier–Stokes equations to provide the wind speed and temperature perturbations. The vertical wind, which is solved by the advection, is implemented and the temperature perturbation acts on the photochemical system.
3 Description of the model outputs
In this section, chemical compositions and emissions computed by the model are presented. We first briefly analyze the outputs of the photochemical model on a 1D grid. The variations of the species allow comparisons with other high altitude 1D studies such as Allen et al. (1981) and Rodrigo et al. (1986) although we do not detain the various models. The evolutions of H and O3 concentrations, sources of the excited OH, are presented in Figure 2. Ozone is strongly affected at high altitude by the photodissociation showing a strong diurnal change. Its production originates from the recombination between O and O2. H is also strongly dependent on the photodissociation of H2O that leads to the increase of H during the day below 80 km (Haefele et al., 2008).
 |
Fig. 2 Examples of molecules concentration evolution, O3 on the left and H on the right. Ozone is strongly dependent on the solar cycle above 60 km. Below 80 km, H originates from the water vapor dissociation. |
The filling of the OH vibrational states from the photochemical resolution shows that the lower energy populations are preferred (Fig. 3) which is consistent with the Maxwell–Boltzmann distribution law although OH is in NLTE. Others studies such as Pickett et al. (2006) or von Savigny et al. (2012) present similar results. We also observe that the altitude of the emission maximum depends on the vibrational level. Higher levels have their maximum at higher altitudes (Moreels et al., 1976).
 |
Fig. 3 Examples of OH vibrational states concentration as function of altitude. |
The temporal VER evolution of the global OH vibrationally excited states along the altitude is represented in Figure 4 (top panel). The airglow emission grows when the night starts, to reach its maximum during the middle of the night. The altitude of the maximum decreases during the night of a few kilometers. We also notice that the airglow layer width decreases as well.
 |
Fig. 4 Top panel: example of the OH volume emission rate (in 105 ph/cm3/s) between 80 km and 95 km for one night (starting at day of year [DoY] 105.8 and ending at DoY 106.2). Bottom panel: same example but with the tidal amplitude doubled. |
In order to investigate the effect of the tidal parameterization and the model sensitivity, the model by doubling the amplitude of the tides. The result is shown in Figure 4 (bottom panel). The maximum occurs in the second part of the night, supported by the compression of the airglow layer. Tides have an effect on the time evolution of the emission, and specifically on the time of the maximum of the emission, on the thickness of the emitted layer, and on the variation of the altitude of the maximum of the emission.
4 Discussions
In this section, we discuss the results by comparing model simulations with past observations reported in the literature, starting with the WINDII instrument observing the OH(8–3) transition, or the P1(3) line (Melo et al., 2000). Since the atmospheric profiles corresponding to these measurements are not available, we cannot reproduce the emission profiles but only obtain a quantitative estimation. Uncertainties through a bootstrap analysis would require in addition uncertainties on the atmospheric profiles and a full line-by-line computation of the spectral emission with its propagation at short temporal intervals.
The model outputs have been filtered to take into account the WINDII instrumental characteristic, centered at 734.6 nm with a spectral width of 1.2 nm. The emission profiles observed and modeled are look-alike, with a maximum for the first at 55 ph/cm3/s and for the second at 80 ph/cm3/s. Analogously, the visible airglow experiment (VAE) (Hays et al., 1973) has observed the OH(8–3) band around 731.6 nm with a spectral width of 1.58 nm. Emission profiles used for the comparison are provided by Abreu & Yee (1989). The maximum has been found at 72 ph/cm3/s for the observation and we established a profile for the same condition of observations with a maximum at 79 ph/cm3/s. The study reported a layer thickness of 12.5 km and our model shows a layer thickness of 10.5 km.
Measurements provided by the SABER instrument aboard the timed platform are compared with the model. SABER is a satellite instrument dedicated to the nightglow observation. The spectral bandwidth ranges between 1575 nm and 1725 nm, and also between 1930 nm and 2170 nm corresponding to ∆ν = 2 transitions (Mlynczak et al., 2013). We present in Figure 5a and b (red solid line) the VER profiles of the airglow emission observed around 1.6 μm and around 2.0 μm respectively for a concordant choice of space and time (orbit 67,574 for the 29th of May 2014). Because SABER data does not provide uncertainty, we selected a time interval of ±1 month around the 29th of May to estimate the mean VER profile (in black) and the standard deviation (in grey) associated to all the profiles included in ±30° in latitude and longitude. The seasonal variation is filtered by a running window of two months to keep information about temporal variability.
 |
Fig. 5 (a) OH 1.6 μm profiles from simulation (in blue), and observations (mean profile in black and closest profile in red). The ±1 standard deviation from the mean is represented with the grey shade. (b) Same as (a) but for OH 2.0 μm. (c) Associated temperature profiles. The simulated temperature profile originates from MSIS data. |
Our simulations underestimate the observations albeit they belong to the range of the standard deviation. In the case of the 1.6 μm VER, the altitude of the peak is consistent with the closest profile but is higher than the mean profile peak. The consistency is increased for the 2.0 μm peak altitude. The difference in the profile-to-profile comparison is useful to highlight the limits of the model. To understand this, the temperature profiles are displayed in Figure 5c. The SABER (mean and closest) and modeled (coming from MSIS data) temperature profiles are represented in black, red and blue respectively. SABER closest temperature profile highlights strong perturbations induced by the presence of gravity waves.
The impact of gravity waves (GW) on the airglow is subject of numerous studies (Taylor et al., 1995a; Pautet et al., 2005, 2014). They act on both the temperature and density of the area where they propagate and they are able to transport energy and momentum up to the mesospheric region. Therefore, changes in temperature and concentrations will lead to changes in emission. For example, a local increase in density can induce a local increase in the observed VER. A change in temperature will imply changes in chemical rates and therefore in OH excited states sources. In this particular case where the simulated VER is lower than observed, we assume that the GW increases the temperature as seen in Figure 5c and modify the density, leading to changes in the chemistry of the nightglow production. Not shown here, the oxygen profile is also larger for the observation in comparison to the observation. This comparison implies that a proper representation of the GW effects in the model is required to recover a more realistic profile of the observed nightglow.
4.1 Comparison with GOMOS data
GOMOS was an instrument on board ENVISAT dedicated to the observation of ozone using the stellar occultation (Bertaux et al., 2010). Airglow data have been obtained by two spectrometers looking at, below and above the star. The complete method is described on Bellisario et al. (2014). GOMOS allowed the recovery of the OH airglow between 925 nm and 955 nm, corresponding to a part of the OH(8–4) band. Chen et al. (2019) uses the R branch between 930 nm and 935 nm to retrieve global nighttime atomic oxygen abundances.
We compare the limb view from GOMOS to the model for several cases (mixing local measurements campaigns with specific locations). Averaged OH(8–4) radiation observed between years 2002 and 2010 over all longitudes have shown a semi-annual variation at the equator, with maxima at the solstices (Bellisario, 2015). Due to the geometry of the occultation observations, the comparison is not straightforward. We would require the spatial evolution of OH emission profiles along the line of sight to estimate the limb radiance by simulation. As a first approximation, we use a homogeneous emission layer and geometrical assumptions for the line of sight limb radiance. The geometrical line of sight is estimated of about 508 km for a layer at 87 km with a width of 10 km. In Figure 6 are represented in red the GOMOS limb radiances and in black the corresponding model simulation limb radiances. For a specific date and location, GOMOS data are averaged (red squares) within the month (to avoid seasonal variations), within a ±15° latitude interval over all longitudes for full dark conditions in most cases (i.e., no light contaminations). The standard deviations of the available spectra within these conditions are represented with the error bars. In addition, the closest observations are added with the red circles.
 |
Fig. 6 In red squares are represented OH(8–4) integrated limb radiances from GOMOS between 925 nm and 955 nm averaged within a month and ±15° latitude for several cases. Corresponding simulations are associated with the black diamonds and the closest observations are in red circles. |
The cases representing the measurements campaigns (detailed in the next section) are shown on the left-hand side and other test cases for specific locations in latitude and time on the right. Overall, the range of simulated limb radiances matches the GOMOS observations. The measurements campaigns do not show a consistent behaviour, with simulated limb radiances increasing for decreasing observations. On the other side, the test cases show consistency with two high cases matching seasonal maxima (T01 and T03 at 0° N, respectively on March 1st, 2014 and October 1st, 2014). T02 (70° N on November 11th) shows a strong decrease in the simulation whereas the observations decrease is fainter. The standard deviation is however higher in this case. T04 and T05 both at 60° S, but respectively on April 15th and July 1st also show consistency with a small decrease.
4.2 Comparison with ground-based observation campaign
During the measurement campaigns performed by ONERA, the main camera used is a short-wave infrared (SWIR) camera. It is based on a thermoelectric cooled InGaAs detector and its spectral bandwidth ranges from 0.9 μm to 1.7 μm (vibrational transitions ∆ν = 2 and 3 of the OH Meinel band system). The integration time is of about 400 ms, for a night with a typical luminosity. The camera is radiometrically calibrated in laboratory in order to get absolute integrated radiance, in photons/s/m2/sr. For the comparison, we integrate the spectral radiance modeled at the ground level between 0.9 μm and 1.7 μm for a zenithal line of sight.
We present the result for two nights, in Figure 7. They correspond to the Observatoire de Haute Provence (OHP, France), 43.93° N, 5.71° O, on March 28th, 2014 and the NARL at Gadanki in India, 13.46° N, 79.18° E on May 29th, 2014. In red are represented the observed radiance at ground level and in black are represented the output of the model.
 |
Fig. 7 (a) Comparisons between the measurement campaign at OHP, France in red and the model in black. (b) Same but for Gadanki, India. The model underestimates in both cases the intensity of the nightglow measured on the ground level, especially at Gadanki, where the night showed a strong activity of gravity waves. |
In the case of OHP, the level of radiation observed varies from 4 × 1014 to 2 × 1014 ph/s/m2/sr with a stair-like evolution whereas the model presents an evolution around 2 × 1014 ph/s/m2/sr. In the case of Gadanki (Fig. 7), the model presents also variations around 2 × 1014 ph/s/m2/sr whereas the evolution observed presents a strong grow from 4 × 1014 to 8 × 1014 ph/s/m2/sr and then it decreases until it reaches 3 × 1014 ph/s/m2/sr. These differences may be due to a strong gravity wave activity that were observed during the campaign and which are not taken into account yet in the model. Specially at Gadanki, we observed the beginning of a strong GW activity temporally correlated with the sharp increase of the radiance at DOY 147.94. A following study will focus on the ground observations performed in Gadanki and the impact of the gravity wave activity seen in the airglow layer.
Several campaigns have been carried at different locations with the same instrument. We present in Figure 8 the evolution of these measurement campaigns (in solid lines) that took places respectively in La Silla (29°15′ S, 70°44′ O, Chile), Pic du Midi (43°55′ N, 5°42′ E, France). The evolutions of most of the nights correspond to a decrease from the beginning of the night and during the second part of the night, we can notice small increases that might originate from tidal effects in Pic du Midi observations. The intensity of the simulated airglow is presented in diamonds and corresponds to the range of observations, between 1 × 1014 and 4 × 1014 ph/s/m2/sr. We relate these differences in intensity and evolution to dynamical effects such as gravity waves and tides. These effects need to be better taken into account in the model to retrieve correctly the evolution of the night airglow.
 |
Fig. 8 Summary of the measurement campaigns (in solid lines) carried out by ONERA. Besides Gadanki and OHP (Fig. 7), campaigns have been performed at La Silla (Chile) and Pic du Midi (France). The crosses represent the evolution of the nightglow modeled at the ground level. |
5 Conclusion
We have developed a numerical model that allows the estimation of the night airglow radiation at ground level. A photochemical model with dynamic modules calculates the evolution of the vibrationally excited OH species. Comparisons with emission and OH density already estimated in past studies show a fairly good overall agreement despite the various uncertainties in the model and the diversified datasets. When confronting the model outputs to SABER data, we relate the differences to the impact of local gravity waves that lead to an increase of the VER at high altitude. Comparisons between the model and high altitude limb observations from space using GOMOS measurements present similar evolution for test cases although local cases require further investigations. To do so, the simulated emission at high altitude is propagated down to the surface for comparison with ground-based observations carried out by ONERA. Night time evolution of the VER shows similar level of intensity with a factor of 2 except over Gadanki where larger differences are reported. In addition, discrepancies in the time evolution can be noted. We suspect that these discrepancies could be due to the large scale dynamic or effects of gravity waves. At this step nor large scale dynamic or gravity waves were explicitly included in the model and should be implemented in further studies (see Swenson & Gardner, 1998; Faivre et al., 2003 or Vargas et al., 2007 for parameterization of gravity waves). An example of anomalies generated by atmospheric tides has shown to perform a significant effect on the evolution and structures of the airglow layer. Nocturnal evolutions with model and observations do not show yet a perfect agreement. To overcome these problems, the inclusion of the present model in a global atmospheric model would allow the simulation to be feed with proper 3D dynamic and atmospheric state.
Acknowledgments
This work was supported by the Direction Genérale de l’Armement (DGA). This work was performed during the course of the ARISE design study (http://arise-project.eu) funded by the European Union’s 7th Framework Programme for Research and Technological Development under Grant Agreement No. 284387. Authors thank the National Atmospheric Research Laboratory (NARL), Observatoire de Haute Provence (OHP), and Observatoire Midi-Pyrenées (OMP) for hosting the measurement campaigns, especially NARL team for the useful comments. Authors thank also Franck Lefèvre for his help on the chemical model. SABER data were acquired from http://saber.gats-inc.com/index.php, GOMOS data used in this study are available to the public at ftp://gomo-ftp-ds.eo.esa.int/ (last access: 1st December 2019) and MSIS model output data are available at https://ccmc.gsfc.nasa.gov/modelweb/models/msis_vitmo.php (last access: 11th February 2020). The editor thanks two anonymous referees for their assistance in evaluating this paper.
Appendix A
Reactions tables
List of the reactions used in the model. Most of the references of the reaction coefficients are taken from Sander et al. (2011).
List of the emissions used in the model and the corresponding radiative lifetimes.
Quantum yields selected for the O2 photodissociation (from Moreels et al., 1977).
Einstein coefficients used in the model to express the reaction coefficients between the excited states of OH (from Turnbull & Lowe, 1989).
List of the reactions used for the chemical heating.
References
- Abreu VJ, Yee JH. 1989. Diurnal and seasonal variation of the nighttime OH (8–3) emission at low latitudes. J Geophys Res 94: 11949–11957. https://doi.org/10.1029/JA094iA09p11949. [CrossRef] [Google Scholar]
- Adler-Golden S. 1997. Kinetic parameters for OH nightglow modeling consistent with recent laboratory measurements. J Geophys Res 102: 19969–19976. https://doi.org/10.1029/97JA01622. [CrossRef] [Google Scholar]
- Allen M, Lunine JI, Yung YL. 1984. The vertical distribution of ozone in the mesosphere and lower thermosphere. J Geophys Res 89: 4841–4872. https://doi.org/10.1029/JD089iD03p04841. [NASA ADS] [CrossRef] [Google Scholar]
- Allen M, Yung YL, Waters JW. 1981. Vertical transport and photochemistry in the terrestrial mesosphere and lower thermosphere /50–120 km/. J Geophys Res 86: 3617–3627. https://doi.org/10.1029/JA086iA05p03617. [CrossRef] [Google Scholar]
- Atkinson R, Welge KH. 1972. Temperature dependence of O(1S) deactivation by CO2, O2, N2, and Ar. J Chem Phys 57: 3689–3693. https://doi.org/10.1063/1.1678829. [NASA ADS] [CrossRef] [Google Scholar]
- Baker DJ, Stair AT Jr. 1988. Rocket measurements of the altitude distributions of the hydroxyl airglow. Phys Scr 37: 611–622. https://doi.org/10.1088/0031-8949/37/4/021. [CrossRef] [Google Scholar]
- Becker KH, Groth W, Schurath U. 1971. The quenching of metastable O2(1∆g) and O2(1Σg+) molecules. Chem Phys Lett 8: 259–262. https://doi.org/10.1016/0009-2614(71)85004-2. [CrossRef] [Google Scholar]
- Bellisario C. 2015. Nightglow modeling at high altitude: Theoretical and observational study, Theses, Université Paris-Saclay, Orsay, France. https://hal.archives-ouvertes.fr/tel-01297329. [Google Scholar]
- Bellisario C, Keckhut P, Blanot L, Hauchecorne A, Simoneau P. 2014. O2 and OH night airglow emission derived from GOMOS-Envisat instrument. J Atmos Ocean Technol 31(6): 1301–1311. https://doi.org/10.1175/JTECH-D-13-00135.1. [CrossRef] [Google Scholar]
- Bertaux JL, Kyrölä E, Fussen D, Hauchecorne A, Dalaudier F, et al. 2010. Global ozone monitoring by occultation of stars: an overview of GOMOS measurements on ENVISAT. Atmos Chem Phys 10: 12091–12148. https://doi.org/10.5194/acp-10-12091-2010. [NASA ADS] [CrossRef] [Google Scholar]
- Brasseur GP, Solomon S. 2005. Aeronomy of the middle atmosphere: Chemistry and physics of the stratosphere and mesosphere. Springer, The Netherlands. [CrossRef] [Google Scholar]
- Burrage MD, Arvin N, Skinner WR, Hays PB. 1994. Observations of the O2 atmospheric band nightglow by the high resolution Doppler imager. J Geophys Res 99: 15017–15024. https://doi.org/10.1029/94JA00791. [CrossRef] [Google Scholar]
- Chabrillat S. 2001. Modélisation du changement global dans l’atmosphère moyenne. URL ftp://ftp.oma.be/dist/simonc/thesis.pdf. [Google Scholar]
- Chamberlain JW, Roesler FL. 1955. The OH bands in the infrared airglow. Astrophys J 121: 541. https://doi.org/10.1086/146015. [CrossRef] [Google Scholar]
- Chen Q, Kaufmann M, Zhu Y, Liu J, Koppmann R, Riese M. 2019. Global nighttime atomic oxygen abundances from GOMOS hydroxyl airglow measurements in the mesopause region. Atmos Chem Phys 19(22): 13891–13910. https://doi.org/10.5194/acp-19-13891-2019. [CrossRef] [Google Scholar]
- Day MJ, Dixon-Lewis G, Thompson K. 1972. Flame structure and flame reaction kinetics. VI. Structure, mechanism and properties of rich hydrogen + nitrogen + oxygen flames. Roy Soc Lond Proc Ser A 330: 199–218. https://doi.org/10.1098/rspa.1972.0140. [CrossRef] [Google Scholar]
- Derelle S, Simoneau P, Deschamps J, Rommeluère S, Hersé M, Moreels G, De Broniol E, Pacaud O. 2012. Development of low-flux SWIR radio-imaging systems to study nightglow emission. In: Infrared technology and applications XXXVIII, Vol. 8353, Andresen BF, Fulop GF, Norton PR (Eds), SPIE, Baltimore, MD, USA. [Google Scholar]
- Didebulidze GG, Lomidze LN, Gudadze NB, Pataraya AD, Todua M. 2011. Long-term changes in the nightly behaviour of the oxygen red 630.0 nm line nightglow intensity and trends in the thermospheric meridional wind velocity. Int J Remote Sens 32: 3093–3114. https://doi.org/10.1080/01431161.2010.541523. [CrossRef] [Google Scholar]
- Faivre M, Moreels G, Pautet D, Keckhut P, Hauchecorne A. 2003. Correlated measurements of mesospheric density and near infrared airglow. Adv Space Res 32: 777–782. https://doi.org/10.1016/S02731177(03)00423-X. [CrossRef] [Google Scholar]
- Fischer CF, Tachiev G. 2004. Breit-Pauli energy levels, lifetimes, and transition probabilities for the beryllium-like to neon-like sequences. Atom Data Nucl Data Tab 87(1): 1–184. https://doi.org/10.1016/j.adt.2004.02.001. http://www.sciencedirect.com/science/article/pii/S0092640X04000087. [Google Scholar]
- Floyd L, Prinz D, Crane P, Herring L. 2002. Solar UV irradiance variation during cycles 22 and 23. Adv Space Res 29(12): 1957–1962. https://doi.org/10.1016/S0273-1177(02)00242-9. [NASA ADS] [CrossRef] [Google Scholar]
- Fomichev VI, Blanchet J-P, Turner DS. 1998. Matrix parameterization of the 15 μm CO2 band cooling in the middle and upper atmosphere for variable CO2 concentration. J Geophys Res 103(11): 505. https://doi.org/10.1029/98JD00799. [Google Scholar]
- Fytterer T, von Savigny C, Mlynczak M, Sinnhuber M. 2019. Model results of OH airglow considering four different wavelength regions to derive night-time atomic oxygen and atomic hydrogen in the mesopause region. Atmos Chem Phys 19(3): 1835–1851. https://doi.org/10.5194/acp-19-1835-2019. [CrossRef] [Google Scholar]
- Gattinger RL, Vallance Jones A. 1973. Observation and interpretation of hydroxyl airglow emissions. In: Physics and chemistry of upper atmospheres, McCormac BM (Ed.), Astrophysics and space science library, Vol. 35, Springer, The Netherlands, 184 p. [CrossRef] [Google Scholar]
- Grygalashvyly M, Sonnemann GR, Lübken F-J, Hartogh P, Berger U. 2014. Hydroxyl layer: Mean state and trends at midlatitudes. J Geophys Res(Atmos) 119(12): 391. https://doi.org/10.1002/2014JD022094. [Google Scholar]
- Haefele A, Hocke K, Kämpfer N, Keckhut P, Marchand M, Bekki S, Morel B, Egorova T, Rozanov E. 2008. Diurnal changes in middle atmospheric H2O and O3: Observations in the Alpine region and climate models. J Geophys Res (Atmos) 113: D17303. https://doi.org/10.1029/2008JD009892. [CrossRef] [Google Scholar]
- Hagan ME, Burrage MD, Forbes JM, Hackney J, Randel WJ, Zhang X. 1999. GSWM-98: Results for migrating solar tides. J Geophys Res 104: 6813–6828. https://doi.org/10.1029/1998JA900125. [CrossRef] [Google Scholar]
- Hays PB, Carignan G, Kennedy BC, Shepherd GG, Walker JCG. 1973. The visible-airglow experiment on atmosphere explorer. Radio Sci 8: 369–377. https://doi.org/10.1029/RS008i004p00369. [CrossRef] [Google Scholar]
- Hedin AE. 1991. Extension of the MSIS thermosphere model into the middle and lower atmosphere. J Geophys Res 96: 1159–1172. https://doi.org/10.1029/90JA02125. [NASA ADS] [CrossRef] [Google Scholar]
- Hines CO. 1960. Internal atmospheric gravity waves at ionospheric heights. Can J Phys 38: 1441. https://doi.org/10.1139/p60-150. [CrossRef] [Google Scholar]
- Hochanadel CJ, Ghormley JA, Ogren PJ. 1972. Absorption spectrum and reaction kinetics of the HO2 radical in the gas phase. J Chem Phys 56: 4426–4432. https://doi.org/10.1063/1.1677885. [CrossRef] [Google Scholar]
- Izod TPJ, Wayne RP. 1968. The formation, reaction and deactivation of O2(1Σ+g). Roy Soc Lond Proc Ser A 308: 81–94. https://doi.org/10.1098/rspa.1968.0209. [CrossRef] [Google Scholar]
- Jacobson MZ. 2005. Fundamentals of atmospheric modeling. Cambridge University Press, New York, NY, USA. [CrossRef] [Google Scholar]
- Kalogerakis K, Pejakovic D, Closser K. 2006. O(1D) relaxation by O(3P). Geophys Res Abstr 8: 9689. [Google Scholar]
- Khomich VY, Semenov AI, Shefov NN. 2008. Airglow as an indicator of upper atmospheric structure and dynamics. Springer-Verlag, Berlin Heidelberg, Germany. [Google Scholar]
- Le Texier H, Solomon S, Garcia RR. 1987. Seasonal variability of the OH Meinel bands. Planet Space Sci 35: 977–989. https://doi.org/10.1016/0032-0633(87)90002-X. [CrossRef] [Google Scholar]
- Leinert C, Bowyer S, Haikala LK, Hanner MS, Hauser MG, et al. 1997. 1997 reference of diffuse night sky brightness (Leinert+ 1998). VizieR Online Data Cat 412: 70,001. [Google Scholar]
- Lindzen RS. 1981. Turbulence and stress owing to gravity wave and tidal breakdown. J Geophys Res 86: 9707–9714. https://doi.org/10.1029/JC086iC10p09707. [CrossRef] [Google Scholar]
- Liu AZ, Swenson GR. 2003. A modeling study of O2 and OH airglow perturbations induced by atmospheric gravity waves. J Geophys Res (Atmos) 108: 4151. https://doi.org/10.1029/2002JD002474. [CrossRef] [Google Scholar]
- Liu G, Shepherd GG. 2006. An empirical model for the altitude of the OH nightglow emission. Geophys Res Lett 33: L09805. https://doi.org/10.1029/2005GL025297. [Google Scholar]
- Lowe RP, Gilbert KL, Turnbull DN. 1991. High latitude summer observations of the hydroxyl airglow. Planet Space Sci 39: 1263–1270. https://doi.org/10.1016/0032-0633(91)90040-H. [CrossRef] [Google Scholar]
- Makhlouf UB, Picard RH, Winick JR. 1995. Photochemical-dynamical modeling of the measured response of airglow to gravity waves 1. Basic model for OH airglow. J Geophys Res 100: 11289–11312. https://doi.org/10.1029/94JD03327. [NASA ADS] [CrossRef] [Google Scholar]
- Makhlouf UB, Picard RH, Winick JR, Tuan TF. 1998. A model for the response of the atomic oxygen 557.7 nm and the OH Meinel airglow to atmospheric gravity waves in a realistic atmosphere. J Geophys Res 103: 6261–6270. https://doi.org/10.1029/97JD03082. [CrossRef] [Google Scholar]
- Marsh DR, Smith AK, Mlynczak MG, Russell JM. 2006. SABER observations of the OH Meinel airglow variability near the mesopause. J Geophys Res (Space Phys) 111: A10S05. https://doi.org/10.1029/2005JA011451. [Google Scholar]
- McDade IC. 1991. The altitude dependence of the OH(X2Π) vibrational distribution in the nightglow – some model expectations. Planet Space Sci 39: 1049–1057. https://doi.org/10.1016/0032-0633(91)90112N. [CrossRef] [Google Scholar]
- Meinel IAB. 1950. OH emission bands in the spectrum of the night sky. Astrophys J 111: 555. https://doi.org/10.1086/145296. [NASA ADS] [CrossRef] [Google Scholar]
- Melo SML, Lowe RP, Russell JP. 2000. Double-peaked hydroxyl airglow profiles observed from WINDII/UARS. J Geophys Res 105: 12397–12404. https://doi.org/10.1029/1999JD901169. [CrossRef] [Google Scholar]
- Mlynczak MG. 1997. Energetics of the mesosphere and lower thermosphere and the SABER experiment. Adv Space Res 20: 1177–1183. https://doi.org/10.1016/S0273-1177(97)00769-2. [CrossRef] [Google Scholar]
- Mlynczak MG. 2000. A contemporary assessment of the mesospheric energy budget. Wash DC Am Geophys Union Geophys Monogr Ser 123: 37–52. https://doi.org/10.1029/GM123p0037. [Google Scholar]
- Mlynczak MG, Hunt LA, Mast JC, Thomas Marshall B, Russell JM, et al. 2013. Atomic oxygen in the mesosphere and lower thermosphere derived from SABER: Algorithm theoretical basis and measurement uncertainty. J Geophys Res (Atmos) 118: 5724–5735. https://doi.org/10.1002/jgrd.50401. [CrossRef] [Google Scholar]
- Mlynczak MG, Solomon S. 1993. A detailed evaluation of the heating efficiency in the middle atmosphere. J Geophys Res 98(10): 517. https://doi.org/10.1029/93JD00315. [Google Scholar]
- Moreels G, Blamont J, Chahrokhi D. 1976. OH emission intensity measurements during the 1969 NASA Airborne Auroral Expedition. J Geophys Res 81: 5467–5478. https://doi.org/10.1029/JA081i031p05467. [CrossRef] [Google Scholar]
- Moreels G, Megie G, Vallance Jones A, Gattinger RL. 1977. An oxygen-hydrogen atmospheric model and its application to the OH emission problem. J Atmos Terr Phys 39: 551–570. [CrossRef] [Google Scholar]
- Mulligan FJ, Nallen JJ. 1998. A search for evidence of tidal activity in OH(3, 1) airglow emissions recorded at Maynooth (53.23° N, 6.35° W). Adv Space Res 21: 831–834. https://doi.org/10.1016/S02731177(97)00683-2. [CrossRef] [Google Scholar]
- Nakajima T, Tanaka M. 1986. Matrix formulations for the transfer of solar radiation in a plane parallel scattering atmosphere. J Quant Spectrosc Radiat Trans 35: 13–21. https://doi.org/10.1016/0022-4073(86)90088-9. [CrossRef] [Google Scholar]
- Nicolet M. 1971. Aeronomic reactions of hydrogen and ozone. In: Models and related experiments, Fiocco G (Ed.), Astrophysics and space science library, Vol. 25, Springer, The Netherlands, , p. 1. [Google Scholar]
- Nicolet M. 1984. On the molecular scattering in the terrestrial atmosphere – an empirical formula for its calculation in the homosphere. Planetary and Space Science 32: 1467. https://doi.org/10.1016/0032-0633(84)90089-8. [CrossRef] [Google Scholar]
- Noxon JF. 1970. Optical Emission from O(1D) and O2(b1Σg) in Ultraviolet Photolysis of O2 and CO2. J Chem Phys 52: 1852–1873. https://doi.org/10.1063/1.1673227. [CrossRef] [Google Scholar]
- Pautet P-D, Taylor MJ, Liu AZ, Swenson GR. 2005. Climatology of short-period gravity waves observed over northern Australia during the Darwin Area Wave Experiment (DAWEX) and their dominant source regions. J Geophys Res (Atmos) 110: D03S90. https://doi.org/10.1029/2004JD004954. [Google Scholar]
- Pautet P-D, Taylor MJ, Pendleton WR, Zhao Y, Yuan T, Esplin R, McLain D. 2014. Advanced mesospheric temperature mapper for high-latitude airglow studies. Appl Opt 53(26): 5934–5943. https://doi.org/10.1364/AO.53.005934. [CrossRef] [PubMed] [Google Scholar]
- Petitdidier M, Teitelbaum H. 1977. Lower thermosphere emissions and tides. Planet Space Sci 25: 711–721. https://doi.org/10.1016/0032-0633(77)90123-4. [CrossRef] [Google Scholar]
- Pickett HM, Read WG, Lee KK, Yung YL. 2006. Observation of night OH in the mesosphere. Geophys Res Lett 33: L19808. https://doi.org/10.1029/2006GL026910. [CrossRef] [Google Scholar]
- Rodrigo R, Lopez-Gonzalez MJ, Lopez-Moreno JJ. 1991. Variability of the neutral mesospheric and lower thermospheric composition in the diurnal cycle. Planet Space Sci 39: 803–820. https://doi.org/10.1016/0032-0633(91)90086-P. [CrossRef] [Google Scholar]
- Rodrigo R, Lopez-Moreno JJ, Moreno F, Lopez-Puertas M, Molina A. 1986. Neutral atmospheric composition between 60 and 220 km – a theoretical model for mid-latitudes. Planet Space Sci 34: 723–743. https://doi.org/10.1016/0032-0633(86)90126-1. [CrossRef] [Google Scholar]
- Rottman G, Woods T, Snow M, DeToma G. 2001. The solar cycle variation in ultraviolet irradiance. Adv Space Res 27(12): 1927–1932. https://doi.org/10.1016/S0273-1177(01)00272-1. [NASA ADS] [CrossRef] [Google Scholar]
- Sander SP, Golden DM, Kurylo MJ, Moortgat GK, Wine PH, et al. 2011. Chemical kinetics and photochemical data for use in atmospheric studies evaluation number 15, Jet Propulsion Laboratory, National Aeronautics and Space Administration, Pasadena, CA, pp. 2011. [Google Scholar]
- Schmidt H, Brasseur GP, Charron M, Manzini E, Giorgetta MA, Diehl T, Fomichev VI, Kinnison D, Marsh D, Walters S. 2006. The HAMMONIA chemistry climate model: Sensitivity of the mesopause region to the 11-year solar cycle and CO2 doubling. J Clim 19: 3903. https://doi.org/10.1175/JCLI3829.1. [CrossRef] [Google Scholar]
- Schott GL. 1960. Kinetic studies of hydroxyl radicals in shock waves. III. The OH concentration maximum in the hydrogen-oxygen reaction. J Chem Phys 32: 710–716. https://doi.org/10.1063/1.1730788. [CrossRef] [Google Scholar]
- Shepherd GG, Thuillier G, Cho Y-M, Duboin M-L, Evans WFJ, et al. 2012. The wind imaging interferometer (WINDII) on the upper atmosphere research satellite: A 20 year perspective. Rev Geophys 50: RG2007. https://doi.org/10.1029/2012RG000390. [CrossRef] [Google Scholar]
- Simoneau P, Derelle S, Rommeluère S, Moreels G, Hersé M. 2011. Modélisation et mesures du rayonnement Nightglow induit par la molécule OH. Tech Rep. No. RT 2/17668 DOTA. [Google Scholar]
- Slanger TG, Cosby PC, Osterbrock DE, Stone RPS, Misch AA. 2003. The high-resolution light-polluted night-sky spectrum at Mount Hamilton, California. Publ Astron Soc Pacific 115: 869–878. https://doi.org/10.1086/376391. [CrossRef] [Google Scholar]
- Slanger TG, Cosby PC, Sharpee BD, Minschwaner KR, Siskind DE. 2006. O(1S → 1D, 3P) branching ratio as measured in the terrestrial nightglow. J Geophys Res: Space Phys 111(A12). https://doi.og/10.1029/2006JA011972. [Google Scholar]
- Smith FL III, Smith C. 1972. Numerical evaluation of Chapman’s grazing incidence integral ch(X, χ). J Geophys Res 77: 3592–3597. https://doi.org/10.1029/JA077i019p03592. [NASA ADS] [CrossRef] [Google Scholar]
- Swenson GR, Gardner CS. 1998. Analytical models for the responses of the mesospheric OH* and Na layers to atmospheric gravity waves. J Geophys Res 103: 6271–6294. https://doi.og/10.1029/97JD02985. [CrossRef] [Google Scholar]
- Takahashi H, Batista PP. 1981. Simultaneous measurements of OH(9,4), (8,3), (7,2), (6,2) and (5,1) bands in the airglow. J Geophys Res 86: 5632–5642. https://doi.org/10.1029/JA086iA07p05632. [CrossRef] [Google Scholar]
- Taylor MJ, Bishop MB, Taylor V. 1995a. All-sky measurements of short period waves imaged in the OI(557.7 nm), Na(589.2 nm) and near infrared OH and O2(0,1) nightglow emissions during the ALOHA-93 campaign. Geophys Res Lett 22: 2833–2836. https://doi.org/10.1029/95GL02946. [CrossRef] [Google Scholar]
- Taylor MJ, Turnbull DN, Lowe RP. 1995b. Spectrometric and imaging measurements of a spectacular gravity wave event observed during the ALOHA-93 campaign. Geophys Res Lett 22: 2849–2852. https://doi.org/10.1029/95GL02948. [CrossRef] [Google Scholar]
- Thekaekara MP. 1974. Extraterrestrial solar spectrum, 3000–6100 Å at 1-Å intervals. Appl Opt 13(3): 518–522. https://doi.org/10.1364/AO.13.000518. [NASA ADS] [CrossRef] [Google Scholar]
- Thomas L, Bowman MR. 1972. The diurnal variations of hydrogen and oxygen constituents in the mesosphere and lower thermosphere. J Atmos Terr Phys 34: 1843–1858. [CrossRef] [Google Scholar]
- Thuillier G, Foujols T, Bolsée D, Gillotay D, Hersé M, et al. 2009. SOLAR/SOLSPEC: Scientific objectives, instrument performance and its absolute calibration using a blackbody as primary standard source. Sol Phys 257(1): 185–213. https://doi.org/10.1007/s11207-009-9361-6. [Google Scholar]
- Trainor DW, Ham DO, Kaufman F. 1973. Gas phase recombination of hydrogen and deuterium atoms. J Chem Phys 58: 4599–4609. https://doi.org/10.1063/1.1679024. [NASA ADS] [CrossRef] [Google Scholar]
- Turnbull DN, Lowe RP. 1989. New hydroxyl transition probabilities and their importance in airglow studies. Planet Space Sci 37: 723–738. https://doi.org/10.1016/0032-0633(89)90042-1. [CrossRef] [Google Scholar]
- Vargas F, Swenson G, Liu A, Gobbi D. 2007. O(1S), OH, and O2(b) airglow layer perturbations due to AGWs and their implied effects on the atmosphere. J Geophys Res (Atmos) 112: D14102. https://doi.org/10.1029/2006JD007642. [CrossRef] [Google Scholar]
- von Savigny C, McDade IC, Eichmann K-U, Burrows JP. 2012. On the dependence of the OH* Meinel emission altitude on vibrational level: SCIAMACHY observations and model simulations. Atmos Chem Phys 12: 8813–8828. https://doi.org/10.5194/acp-12-8813-2012. [CrossRef] [Google Scholar]
- Wiese WL, Fuhr JR, Deters TM. 1996. Atomic transition probabilities of carbon, nitrogen, and oxygen: A critical data compilation. American Chemical Society and American Institute of Physics for the National Institute of Standards and Technology, Washington, DC and Woodbury, NY. [Google Scholar]
- Yee J-H, Crowley G, Roble RG, Skinner WR, Burrage MD, Hays PB. 1997. Global simulations and observations of O(1S), O2(1Σ) and OH mesospheric nightglow emissions. J Geophys Res 102: 19949–19968. https://doi.org/10.1029/96JA01833. [CrossRef] [Google Scholar]
- Young RA, Black G. 1966. Excited-state formation and destruction in mixtures of atomic oxygen and nitrogen. J Chem Phys 44: 3741–3751. https://doi.org/10.1063/1.1726529. [CrossRef] [Google Scholar]
Cite this article as: Bellisario C, Simoneau P, Keckhut P & Hauchecorne A 2020. Comparisons of spectrally resolved nightglow emission locally simulated with space and ground level observations. J. Space Weather Space Clim. 10, 21.
All Tables
List of the species used in the present model. Excited states are used for OH (all vibrational, from 1 to 9), and also O2(1∆), O2(1Σ), O(1D), and O(1S).
List of the reactions used in the model. Most of the references of the reaction coefficients are taken from Sander et al. (2011).
List of the emissions used in the model and the corresponding radiative lifetimes.
Quantum yields selected for the O2 photodissociation (from Moreels et al., 1977).
Einstein coefficients used in the model to express the reaction coefficients between the excited states of OH (from Turnbull & Lowe, 1989).
All Figures
 |
Fig. 1 Example of a spectrum at 87 km (in red) and the same spectrum propagated at the ground level (in black). We notice the strong water vapor absorption band around 1.4 μm. |
| In the text | |
 |
Fig. 2 Examples of molecules concentration evolution, O3 on the left and H on the right. Ozone is strongly dependent on the solar cycle above 60 km. Below 80 km, H originates from the water vapor dissociation. |
| In the text | |
 |
Fig. 3 Examples of OH vibrational states concentration as function of altitude. |
| In the text | |
 |
Fig. 4 Top panel: example of the OH volume emission rate (in 105 ph/cm3/s) between 80 km and 95 km for one night (starting at day of year [DoY] 105.8 and ending at DoY 106.2). Bottom panel: same example but with the tidal amplitude doubled. |
| In the text | |
 |
Fig. 5 (a) OH 1.6 μm profiles from simulation (in blue), and observations (mean profile in black and closest profile in red). The ±1 standard deviation from the mean is represented with the grey shade. (b) Same as (a) but for OH 2.0 μm. (c) Associated temperature profiles. The simulated temperature profile originates from MSIS data. |
| In the text | |
 |
Fig. 6 In red squares are represented OH(8–4) integrated limb radiances from GOMOS between 925 nm and 955 nm averaged within a month and ±15° latitude for several cases. Corresponding simulations are associated with the black diamonds and the closest observations are in red circles. |
| In the text | |
 |
Fig. 7 (a) Comparisons between the measurement campaign at OHP, France in red and the model in black. (b) Same but for Gadanki, India. The model underestimates in both cases the intensity of the nightglow measured on the ground level, especially at Gadanki, where the night showed a strong activity of gravity waves. |
| In the text | |
 |
Fig. 8 Summary of the measurement campaigns (in solid lines) carried out by ONERA. Besides Gadanki and OHP (Fig. 7), campaigns have been performed at La Silla (Chile) and Pic du Midi (France). The crosses represent the evolution of the nightglow modeled at the ground level. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


