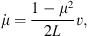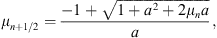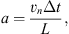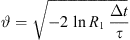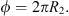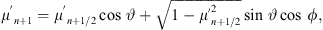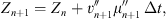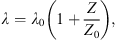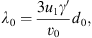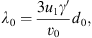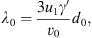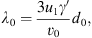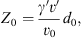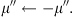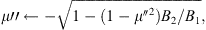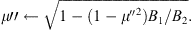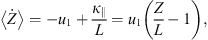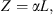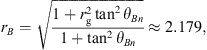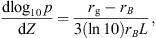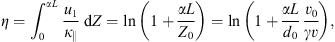| Issue |
J. Space Weather Space Clim.
Volume 14, 2024
Topical Issue - CMEs, ICMEs, SEPs: Observational, Modelling, and Forecasting Advances
|
|
|---|---|---|
| Article Number | 15 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/swsc/2024012 | |
| Published online | 28 May 2024 | |
Research Article
Effects of adiabatic focusing and free-escape boundaries in coronal shock acceleration
1
Department of Physics and Astronomy, University of Turku, 20014 Turku, Finland
2
Centre for mathematical Plasma Astrophysics (CmPA)/Department of Mathematics, KU Leuven, B-3001 Leuven, Belgium
3
Institute of Physics, University of Maria Curie-Skłodowska, Pl. M. Curie-Skłodowskiej 5, 20-031 Lublin, Poland
* Corresponding author: lidiya.l.anniejohn@utu.fi
Received:
6
October
2023
Accepted:
4
April
2024
Solar energetic particles (SEPs) are considered a serious radiation threat to space technologies and humans in space. SEPs are accelerated to high energies by solar explosive phenomena such as solar flares and in particular by shocks driven by coronal mass ejections (CMEs). We aim to better understand the effects of magnetic field gradient-induced adiabatic focusing on the coronal acceleration of SEPs and to test whether free-escape boundaries produce the same effects as focusing. We present results from a one-dimensional oblique shock model with a mean free path similar to Bell’s (1978) theory using Monte Carlo simulations. We show that the momentum spectrum at a shock and far upstream will attain a steady state in a model with adiabatic focusing, whereas it does not in a non-focusing model. However, the effects of focusing can be mimicked in a non-focused simulation by introducing a free-escape boundary ahead of the shock close to the position where the particles will escape from the shock by focusing in a focused transport simulation. This provides a promising avenue for constructing computationally efficient codes that can model the particle emission from shocks.
Key words: Solar energetic particles / Shock waves
© L. Annie John et al., Published by EDP Sciences 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Large gradual solar energetic particle (SEP) events (e.g., Desai & Giacalone, 2016) are huge outbursts of energetic particle radiation from the Sun and the cause of solar radiation storms that are one of the key components of space weather (e.g., Vainio et al., 2009). While solar flares probably contribute to the fluxes of SEPs in large gradual events, their primary cause is believed to be diffusive shock acceleration (DSA) (Axford et al., 1977; Krymskii, 1977; Bell, 1978; Blandford & Ostriker, 1978) in coronal and interplanetary shocks driven by coronal mass ejections (CMEs) (e.g., Reames, 2023). Thus, recent space weather modeling of SEP events is built on tracing particles in heliospheric plasma that is being traversed by the CME-driven shock (e.g., Wijsen et al., 2022, 2023; Ding et al., 2022).
One of the key factors affecting the efficiency of DSA is the upstream turbulence that provides particles an opportunity to be scattered back to the shock from the upstream region. While the downstream medium (which for CME-driven shocks is towards the Sun from the shock) is naturally turbulent and provides for fast isotropisation of the distributions, the upstream region has much less fluctuations. In fact, the ambient scattering mean free paths in the inner heliosphere at MeV to hecto-MeV energies are of the order of 0.1 AU (Palmer, 1982; Bieber et al., 1994), which is too large to account for efficient acceleration of protons to deca-MeV energies via the diffusive mechanism (Vainio, 2006). Thus, models must somehow account for a foreshock region that is more turbulent than the medium far upstream. However, turbulent foreshock models must also meet the requirement that particles can escape from the system since they are often detected at Earth some tens of minutes after the lift-off of the CME. Fortunately, streaming energetic particles themselves can drive Alfvén waves unstable in the foreshock region (Bell, 1978), thus providing for a way to organize the turbulent structure ahead of the shock in a manner that allows for both the rapid acceleration of particles and their subsequent escape towards the observer. This process has been modeled by several teams of authors in the context of SEPs (e.g., Lee, 1983; Gordon et al., 1999; Rice et al., 2003; Li et al., 2005; Vainio & Laitinen, 2007; Ng & Reames, 2008; Afanasiev et al., 2015; Berezhko & Taneev, 2016; Fraschetti, 2021).
The models of SEP acceleration with self-generated turbulence can be divided into local and global models. Local models consider a simulation domain close to the shock, where the plasma properties in the upstream region are homogeneous and the system can be formulated in terms of one-dimensional particle and wave transport equations (e.g., Lee, 1983; Gordon et al., 1999; Ng & Reames, 2008; Afanasiev et al., 2015, 2023; Fraschetti, 2021). Global models (e.g., Vainio & Laitinen, 2007; Berezhko & Taneev, 2016) take into account the global geometry of the magnetic field and the decrease of density in the upstream region, which can lead to time-dependent models of the evolving SEP acceleration process, as the shock propagates through the variable medium. However, a hybrid approach is also often used (e.g., Rice et al., 2003; Li et al., 2005; Hu et al., 2017), where the wave generation process is considered in a sheet ahead of the shock front (often analytically) to account for the rapid particle acceleration process, but the global transport of the particles is still computed under the test-particle assumption, i.e., without considering the wave growth. This approach has great potential in operational space weather modeling, as it leads to a considerably smaller need for computational resources than models that simulate the whole system self-consistently. The coupling approach is certainly not as accurate as a fully self-consistent model, but can avoid prohibitively long running times that prevent self-consistent models from being used in real time in large SEP events that produce strong foreshock wave fields and very short mean free paths close to the shock. The coupling of the two domains, however, requires care because the particle population escaping from the acceleration region should correspond to the self-consistently computed flux of escaping particles.
In a one-dimensional (1-D) system with an infinite extent of the upstream region, particle intensities far upstream from the shock tend towards zero even in the steady state. This is because all particles will eventually return to the shock as a result of isotropisation in the upstream plasma resulting in advection towards the shock. This also means that a steady state will never be reached for the entire energy spectrum: particles are accelerated to higher and higher energies indefinitely, resulting in a cut-off energy in the spectrum that increases over time without a limit. SEPs, however, are able to escape from the acceleration site and propagate very rapidly to the observer in near-Earth space. The physical process that can facilitate the escape is adiabatic focusing (Roelof, 1969) that, due to the conservation of the first adiabatic invariant, causes particle velocities to align with the magnetic field in the direction of the decreasing magnetic field magnitude, i.e., away from the Sun. In local modeling, particles can escape to the far upstream only if the upstream region of the shock has a finite size, i.e., if there is a free-escape boundary at some distance away from the shock. In global modeling, the free-escape boundary is used as well. For example, in the iPATH model, the free-escape boundary is assumed to be proportional to the diffusion length with the coefficient of proportionality to be 4 (e.g., Hu et al., 2017) or being a function of energy (Ding et al., 2024). In the latter case, the energy dependence is obtained through the fitting of observed intensities by the solution of a modified 1-D Parker equation that includes an escape term (but does not consider the adiabatic focusing explicitly).
The purpose of this paper is to investigate particle escape from a shock wave numerically using two kinds of models: one with a finite and homogeneous upstream region and thus no focusing, and another with a weakening magnetic field causing particles to escape through the effect of focusing. We will study the one-dimensional model and investigate how well the particle escape from the finite upstream region will mimic the effect of focusing in the weakening field. In this initial study, we will keep the shock parameters constant over time and consider a simplified ambient medium where also the scale height of the magnetic field magnitude is constant, resulting in a spatially constant rate of focusing. Because of the simplicity of the applied model, the study should be taken as a first step in the comparative evaluation of the effects of focusing and free-escape boundaries on DSA. Further modeling studies in more realistic settings are required to obtain final results for the correct coupling of the local acceleration models to the global transport models.
The paper has the following structure: in Section 2, we present the numerical model and the investigated shock scenario; in Section 3, we present the results; in Section 4, we discuss the results; and in Section 5, we provide the conclusions of the study.
2 Simulation model
We consider particle transport and acceleration in a simplified scenario of a shock wave propagating through a stationary stratified medium like the solar corona. In our simulation model, an oblique shock is propagating outwards from the Sun at a speed Vs measured along the magnetic field line. The shock obliquity angle between the shock normal and the magnetic field is θBn. For simplicity, we take the shock to be strong, i.e., we take its gas compression ratio to be rg = 4, and the transverse magnetic field components to be compressed by the same factor (e.g., Decker, 1988). The magnetic field line under consideration is assumed to be straight and along the z-coordinate as seen in Figure 1, measured in the frame fixed to the Sun. The inhomogeneous upstream magnetic field has a magnitude that exponentially decreases with altitude, B(z) = B0e−z/L, where L = −B/(∂B/∂z) is the magnetic scale length, i.e., the focusing length (see, e.g., Vainio et al., 2000). Here the focusing length is assumed to be constant due to simplicity, but in more realistic coronal modelling it should increase outwards in particular at distances where open field lines constitute most of the flux. The particles are transported along z in a one-dimensional simulation box (see Fig. 1) under the influence of focusing and scattering due to magnetic irregularities that are taken to be frozen-in into the plasma.
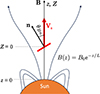 |
Figure 1 Depiction of the one-dimensional simulation geometry, where an oblique shock propagates along a diverging magnetic field B away from the solar surface with a shock obliquity θBn and speed Vs along the modeled magnetic field line. The model is simulated along z (origin at the solar surface) and the magnetic field strength depends on it by B(z) = B0e−z/L. Z is measured along z, but Z = 0 is fixed at the shock. |
The particle tracer utilizes the Monte Carlo method. We follow the particles under the guiding center approximation in the mean magnetic field in small time steps and perform scatterings caused by magnetic fluctuations after each time step using a pseudo-random generator. The processes of magnetic focusing, pitch-angle scattering, and particle propagation are implemented consecutively (in this order). The effect of focusing on the pitch angle is given by (Roelof, 1969)
where μ and v are the particle’s pitch-angle cosine and speed measured in the solar frame, where the process conserves the energy assuming that the magnetic field is static. In the code, the new pitch-angle cosine after magnetic focusing is calculated (using an implicit Euler method):
with
where Δt is the time step, and vn and μn are the particle speed and pitch-angle cosine, measured in the solar frame, at the beginning of the nth time step. The use of the implicit method ensures that μ stays inside the physical range of μ ∈ [−1, 1]. (We apply the same rate of focusing also on the downstream side of the shock, although there the assumptions for its use are strictly valid only for a fully parallel shock.) Particles are then scattered elastically and isotropically in the local plasma rest frame. The new pitch-angle cosine due to small-angle scattering is calculated by using the scattering angle (ϑ), phase angle (ϕ), and a collision time, τ = λ/v, where λ is the scattering mean free path (see Eq. (8)). Pseudo-random numbers R1 and R2 from a uniform distribution between 0 and 1 are used for the computation of the scattering and phase angles in the plasma rest frame as follows (e.g., Vainio et al., 2000):
The pitch-angle cosine after the scattering is then calculated from
where the primes denote that the values are to be given in the local plasma frame. Isotropic scattering is the simplest scattering model and easiest to implement at high numerical accuracy (Vainio et al., 2000). Finally, particles are moved along the mean magnetic field by
where Zn is the particle position in the beginning of the time step in the frame co-moving with the shock (which is at Z = 0) and, thus, the speed 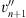 and pitch-angle cosine
and pitch-angle cosine 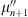 are also given in the shock frame. In processes changing the pitch angle of the particle, we always apply the frame where particle energy is conserved. The changes of pitch angle will then lead to the energy changes in other frames of reference. In particular, focusing will lead to a decrease of energy in the plasma frame if the flow is towards the weaker magnetic field, resulting in adiabatic cooling (Ruffolo, 1995).
are also given in the shock frame. In processes changing the pitch angle of the particle, we always apply the frame where particle energy is conserved. The changes of pitch angle will then lead to the energy changes in other frames of reference. In particular, focusing will lead to a decrease of energy in the plasma frame if the flow is towards the weaker magnetic field, resulting in adiabatic cooling (Ruffolo, 1995).
A mean free path similar to the theory of Bell (1978) for the case of strong shocks is used to compute the scattering rate in the upstream region (see also Vainio & Laitinen, 2007; Vainio et al., 2014):
where Z is the distance along the magnetic field measured from the shock,
is the mean free path at the shock, and
is a characteristic width of the foreshock turbulence region, while v′, v0, and γ′ are the (plasma-frame) speed, injection speed, and Lorentz factor of the particle, respectively, and u1 is the plasma flow speed in the de Hoffmann – Teller (HT) frame (i.e., u1 = Vs for an upstream medium at rest). The mean free path increases linearly away from the shock in the upstream but the energy dependence is more involved. At the shock, the mean free path is proportional to the Lorentz factor of the particles, but further out from the shock (Z ≫ Z0) it is inversely proportional to the particle speed. In Bell’s model, d0 is related to plasma parameters and the density of seed particles, but here we treat it as a free parameter. On the downstream side of the shock, we take the value of λ = λ0 independent of distance. Since we treat d0 as a free parameter, the model is not self-consistent but contains the main features of the self-generated foreshock structure to allow for the assessment of the role of focusing and its similarity to the effects of a free-escape boundary. We use fully relativistic transformations between the frames of reference so particle transport and acceleration is treated correctly also at relativistic energies and high obliquities of the shock.
Mono-energetic protons (at v′ = v0) are injected just upstream of the shock at a constant rate throughout the simulation. The injection is considered to be isotropic in the upstream plasma rest frame, i.e., a random pitch-angle cosine in the range of μ′ ∈ [−1, 1] is assigned to the particle initially. Particles interact with the shock in the HT frame and are accelerated in the shock crossings as described in the DSA theory (e.g., Drury, 1983). When the particle interacts with the shock, we assume that its first adiabatic invariant is conserved. While the adiabatic approximation formally requires the field to change only slightly over the particle gyroradius, full-orbit simulations in a step-like shock show that the first adiabatic invariant is conserved statistically in shock–particle interactions (Decker, 1988). Adiabatic approximation of shock crossings in the microscopic treatment of shocks also leads to the same steady-state accelerated particle spectrum at the shock as a macroscopic treatment of the DSA (Drury, 1983), so it can be regarded as a reasonable practical assumption. A fraction of the particles that are incident on the shock from the upstream side are reflected because of their inability to penetrate the magnetic mirror, and their pitch-angle cosine measured in the HT frame changes sign:
Those that are in the loss cone going downstream have their pitch angles changed according to
because of the higher magnetic field in the downstream, B2, than in the upstream, B1. (The loss-cone boundary is obtained by setting the quantity below the square root to zero.) Particles incident on the shock from the downstream side are all transmitted to the upstream and their pitch angles are focused along the field to conserve the adiabatic invariant:
The changes in the pitch angle in the shock interactions are elastic in the HT frame. Particle acceleration at the shock is a result of head-on collisions of the particles with the shock as well as head-on collisions with the scattering centres converging at the shock, as has been established in the microscopic derivation of DSA by Drury (1983).
Adiabatic focusing drives particles towards the far upstream and causes adiabatic cooling in the downstream, where the plasma velocity in the solar frame is non-zero (Ruffolo, 1995). When simulating the case without focusing, the new pitch-angle cosines caused by magnetic focusing are not considered (i.e., μn+1/2 = μn), but all other parameters and processes remain the same. In this case, however, we introduce a free-escape boundary at a fixed distance upstream of the shock and study whether the effects of focusing could be reproduced by including such a boundary. When the particles cross the free-escape boundary, they are removed from the simulation.
The bulk velocity of SEPs, caused by a balance of focusing and scattering processes, is directed along the magnetic field and its magnitude is given by κ∥/L, where 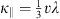 is the spatial diffusion coefficient (Kocharov et al., 1996). In our mean free path model (consistent with Bell’s theory), the spatial diffusion coefficient far away from the shock is κ∥ = u1Z. Additionally, particles get advected with turbulence towards the shock at speed u1. Thus, the total shock-frame particle advection velocity in the far upstream region is
is the spatial diffusion coefficient (Kocharov et al., 1996). In our mean free path model (consistent with Bell’s theory), the spatial diffusion coefficient far away from the shock is κ∥ = u1Z. Additionally, particles get advected with turbulence towards the shock at speed u1. Thus, the total shock-frame particle advection velocity in the far upstream region is
which equals zero at Z = L. Thus, at greater distances particles are advected outwards from the shock and their return back to the shock becomes more and more unlikely. We, therefore, set the free-escape boundary at a distance,
where α is a free parameter of order unity.
3 Results
We carried out simulations for 2 ∙ 107 particles with a total simulation time of 2000 R⊙/c, which corresponds to about 77 min in real-time. The magnetic focusing length is set to L = R⊙. The adopted shock obliquity is θBn = 30°, the shock speed relative to upstream plasma u1 = 0.004 c, and the particle injection speed v0 = 0.0048 c. The gas compression ratio of the shock, rg = 4, gives the magnetic compression ratio as
with the assumption that the tangential field components are compressed by the same factor as the density, consistent with the large Mach number of the shock (e.g., Decker, 1988).
In Figure 2, the temporal evolution of upstream and downstream fluxes as a function of position and momentum inside the simulation box are displayed, separately for the case with no focusing (left column), with focusing (middle column), and without focusing but with a free-escape boundary at Z = L (i.e., α = 1; right column). The shock is at Z = 0, and the positive Z-coordinate denotes the upstream.
 |
Figure 2 Particle distributions at different times in simulations without focusing (left column), with focusing (middle column), and with a free-escape boundary in the upstream at Z = αL, α = 1 (right column) for an oblique shock propagating outwards from the Sun along an exponentially decreasing magnetic field. The horizontal dotted lines give the injection momentum, and the dashed line in panel (h) gives a characteristic curve for an advecting downstream population undergoing adiabatic cooling. The horizontal stripes in the distributions result from the consecutive interactions of the initially mono-energetic particles with the shock. |
It is clearly observed that magnetic focusing has a major effect on the particle acceleration mechanism. While the particles in the non-focused system are continuously accelerated to higher momenta with larger simulation times, those in the focused system seem to reach a steady state in momentum close to the shock. Magnetic focusing, as anticipated, drives particles away from the shock towards the far upstream (cf. Vainio et al., 2000; Vainio & Laitinen, 2007). Therefore, strong particle escape towards far upstream is observed in the focused system. Additionally, in the downstream of the focused system (see Fig. 2 panel h), the logarithm of the momentum shows a linear relationship with the distance from the shock in accordance with expectations for adiabatic cooling at a constant rate (since focusing length is constant in our model), as particles are advected with the flow towards the downstream (Vainio et al., 2000). The non-focused system exhibits stronger particle acceleration throughout the simulation in comparison with the focused case due to the absence of the maximum-energy-limiting escape and cooling. However, when considering the free-escape boundary system, the maximum momentum of the particles attained upstream is very similar to that in the focused system. This constitutes the main new finding of our study.
To investigate the maximum energy attained in a simulation as a function of time in more detail, particles are simulated until t = 3000 R⊙/c with intermediate outputs every 250 R⊙/c. The observed cutoff energies, Ec, of the energy distribution at −0.05 < Z/R⊙ < 0 as a function of time for the non-focused, focused, and free-escape boundary systems are plotted in Figure 3. The cutoff energies are determined assuming that the energy distribution follows 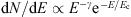 , where γ = 3/2 is the value of the spectral index in a strong shock at non-relativistic energies. Instead of fitting the binned energy distribution with the functional form, we form the weighted cumulative distribution of the particles (with
, where γ = 3/2 is the value of the spectral index in a strong shock at non-relativistic energies. Instead of fitting the binned energy distribution with the functional form, we form the weighted cumulative distribution of the particles (with 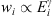 and i numbering the particles in ascending order of energy) inside the spatial range and calculate the 63.2nd percentile of this distribution (which would correspond to the characteristic energy of an exponential distribution). The cutoff energies are plotted in the units of upstream ram energy,
and i numbering the particles in ascending order of energy) inside the spatial range and calculate the 63.2nd percentile of this distribution (which would correspond to the characteristic energy of an exponential distribution). The cutoff energies are plotted in the units of upstream ram energy, 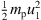 , where mp is the proton mass and u1 is the upstream flow speed in the HT frame. The cutoff energy in the non-focused system is observed to be increasing indefinitely, whereas the cutoff energies in the focused case and free-escape boundary cases attain steady states at around t = 2000 R⊙/c. In addition, in the non-focused and free-escape boundary cases, due to the absence of adiabatic cooling, the cutoff energies are higher than in the focused case at the initial intermediate times. The steady-state cutoff energy in the focused case seems consistent with a free-escape boundary case, where 0.67 < α < 1, with the best fit provided with α = 0.8.
, where mp is the proton mass and u1 is the upstream flow speed in the HT frame. The cutoff energy in the non-focused system is observed to be increasing indefinitely, whereas the cutoff energies in the focused case and free-escape boundary cases attain steady states at around t = 2000 R⊙/c. In addition, in the non-focused and free-escape boundary cases, due to the absence of adiabatic cooling, the cutoff energies are higher than in the focused case at the initial intermediate times. The steady-state cutoff energy in the focused case seems consistent with a free-escape boundary case, where 0.67 < α < 1, with the best fit provided with α = 0.8.
 |
Figure 3 The cutoff energies (see text for details) of the particles as a function of simulation time for no focusing, focusing, and different free-escape boundary simulation cases close to the shock in the downstream region (−0.05 R⊙ < Z < 0). The location of the free-escape boundary in the upstream of the shock is given by Z = αL, where L = R⊙. |
Next, we analyze the particle momentum spectra in the downstream close to the shock (−0.05 R⊙ < Z < 0) at the time when the focused case has attained a steady state, see Figure 4. The downstream spectrum for the non-focused case shows a power-law dependence well below the momentum cutoff, as predicted by the DSA theory (see, Bell, 1978), and the spectrum with the exponential cut-off in energy, exp(−E/Ec), multiplying the power law is shown in figure, as well. (Note that this is not fit to the spectrum but utilises the cut-off energy determined by the method described above.) This case produced the highest cutoff momentum. In the other cases, spectral cutoffs occur at lower momenta so the power-law part of the spectrum is less visible. Various α values for the free-escape boundary conditions are considered to investigate which of the values provides a more similar result with the focused case. The case with α = 0.8 presents the most similar spectrum to the focused case. A higher-α free-escape boundary shows higher cutoff momenta.
 |
Figure 4 The momentum distributions of the particles in downstream close to the shock (−0.05 R⊙ < Z < 0) for no focusing, focusing, and different free-escape boundary simulation cases at a given simulation time, where the focusing and free-escape boundary cases have reached a steady state. The grey dashed line is the canonical power-law of the steady-state DSA theory and the dotted curve on the no-focusing distribution represents the product of the power-law spectrum with the exponential cut-off in energy, exp(−E/Ec). |
Figure 5 shows the momentum distribution of the particles that have escaped towards the upstream through the free-escape boundary and, in the focused case, the particles that have moved far away (Z > L) from the shock in the upstream region, where the mean advection velocity points away from the shock. We observe that for all systems, the cutoff energies first increase. At t = 2000 R⊙/c, the distributions in all cases, apart from α = 1.5 (see also Fig. 3), have already attained their steady-state form. The higher α values take more time to show the steady state condition as the particles keep accelerating further, compared to lower α values. For the escaping particles, the best fit between the focused and the non-focused cases is obtained with α = 0.67 in the steady state. The energy attained by the focused case is low, because when a particle moves to downstream it loses energy as it returns back to the shock. During earlier times, however, the focused spectrum is not consistently represented by any particular value of α, as the shapes of the distributions for the different cases evolve differently.
 |
Figure 5 The momentum distributions of the escaping particles in the focusing and free-escape boundary simulations at different points in simulation time. In the focusing simulation, a particle will unlikely return to the shock from Z > L, so particles beyond L upstream will be considered for the momentum distributions of escaped particles. In the free-escape boundary simulations, particles that are beyond the free-escape boundary specified by Z = αL (where L = R⊙) are considered for the momentum distributions of escaped particles. |
4 Discussion
The results of the simulations agree with the fact that the particle escape from the non-focused model with a homogeneous and finite upstream region mimics the focused model with a weakening magnetic field. We can compare the fluxes as a function of position and momentum for the focused, non-focused, and free-escape boundary systems in Figure 2. The adiabatic focusing causes strong particle escape outwards from the Sun towards upstream, as well as adiabatic cooling in the downstream. As particles propagate upstream, adiabatic focusing (Eq. (2)) gradually prevails over pitch-angle scattering due to the increasing mean free path (Eq. (8)), while the focusing length remains constant in our model. Consequently, beyond a certain distance, adiabatic focusing becomes dominant to such an extent that scattering fails to redirect the particles back to the shock, leading to the escape of particles from the system.
In the non-focused system, however, the pitch angle scattering causes particles to, eventually, always return back to the shock from upstream. Hence, as time elapses, particles in the system accelerate to higher energies indefinitely (see also Figs. 3 and 4). Moreover, in the non-focused system, particles will conserve plasma-frame energy during propagation but as they move further downstream, they will not return back to the shock, and they will also not show particle escape to the far upstream.
Scattering conserves the energy in the local plasma rest frame while focusing conserves energy in the frame where the mean magnetic field is static (Ruffolo, 1995). Focusing on the downstream region leads to adiabatic cooling and mirroring when the particles try to approach the Sun. Thus, particle energy is reduced during downstream propagation. After a certain simulation time, as observed in Figure 3, particles escape and adiabatic cooling balances particle acceleration to produce a steady state in the focused case. In Figure 2 panel h, the observed advecting particle population undergoes cooling at a rate 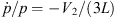 , where V2 = Vs − u2 is the downstream solar-frame advection speed and u2 = u1rB / rg is the shock-frame advection speed. Converting the time derivative to a spatial gradient using the downstream shock-frame advection speed gives a characteristic curve for an advecting population in the (Z, log10 p) plane in form
, where V2 = Vs − u2 is the downstream solar-frame advection speed and u2 = u1rB / rg is the shock-frame advection speed. Converting the time derivative to a spatial gradient using the downstream shock-frame advection speed gives a characteristic curve for an advecting population in the (Z, log10 p) plane in form
which matches well with the low-energy downstream population of the focused simulation (see Fig. 2). At higher energies, particles cool at the same rate but are also diffusing spatially, so the effect is less clear in the (Z, log10 p) plane.
Even though adiabatic cooling as a result of adiabatic focusing is absent in the free-escape boundary system, a steady state cutoff in momentum is still achieved. This is attributed to the fact that the particle escape through the free-escape boundary in the upstream at Z = αL (see Fig. 2 right column for the case of α = 1) balances with the particle acceleration. This results in a steady-state cutoff energy, where the number of diffusion lengths in the upstream region,
becomes of unit order (Vainio et al., 2000), i.e., when γv/v0 ∼ αL/d0; values of η lower than about 2 will lead to a softening of the spectrum and a steady-state cutoff is established in the spectrum, since η decreases with particle momentum (see Fig. 5). Note that in a model with a solar wind in the ambient plasma, adiabatic cooling in the focused case would occur also in the upstream region, which would likely lead to a lower value of α that produces the best comparison of the spectrum in the focused and the free-escape boundary cases.
It is still an open question whether the system can truly attain the steady state. In our model, the shock has to travel a long distance before that occurs: the distance travelled by the shock (at Vs = 0.004 c) for a simulation time of t = 2000 R⊙/c is 8 R⊙, which is large compared to the adopted constant value of L = R⊙. A simulation with a time-dependent shock and a more realistic model of the background field and coronal plasma would be able to address this question. One could, however, expect a positive outcome of the modelling: according to SEP observations, emission of the highest-energy protons occurs while the shock is still in the corona, and the acceleration does not lead to an ever-increasing maximum energy at the observer (e.g., Reames, 2023). This is consistent with the acceleration and loss processes reaching a balance at an energy, which evolves towards lower values over time.
With our choice of d0 = 0.05 R⊙ particles are not accelerated to very high energies. The ram energy is 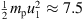 keV, so the energy cutoffs in simulations shown in Figure 3 are in the MeV range. However, we expect the cutoff momentum to be inversely proportional to d0 (see above) so choosing a lower value will increase the steady-state maximum energy correspondingly. The acceleration rate is inversely proportional to λ0, which is proportional to d0, so the rate will scale in the same proportion to d0 as the maximum energy. Thus, the time it takes for the system to achieve a steady state is not affected by the choice of d0.
keV, so the energy cutoffs in simulations shown in Figure 3 are in the MeV range. However, we expect the cutoff momentum to be inversely proportional to d0 (see above) so choosing a lower value will increase the steady-state maximum energy correspondingly. The acceleration rate is inversely proportional to λ0, which is proportional to d0, so the rate will scale in the same proportion to d0 as the maximum energy. Thus, the time it takes for the system to achieve a steady state is not affected by the choice of d0.
The model of the upstream mean free path is based on the momentum and spatial dependence of the self-consistent theory of Bell (1978) for a strong shock. However, as we do not relate the parameter d0 to the properties of plasma and particle injection rate, we do not consider the model in a self-consistent form. Furthermore, these dependencies are not universal, i.e., other self-consistent models predict different dependencies on Z and p (e.g., Afanasiev et al., 2015). Finally, our mean free path model is time-independent, which would also not be the case in a fully self-consistent, time-dependent model (Vainio & Laitinen, 2007; Afanasiev et al., 2015). Thus, choosing the location of the free-escape boundary in the model to really accurately mimic the effect of focusing requires a careful consideration of the model parameters in the foreshock. In any case, however, it should be similar to the distance at which κ∥/L ∼ u1, regardless of the mean free path in the foreshock. In our model, values of α somewhat below unity seem to best represent the focusing case, but the actual value we would choose depends on whether we want to model the spectrum at the shock or the escaping spectrum. For the possible space weather applications, these would correspond to the early phases of the SEP event or to the in-situ shock crossing, respectively.
Finally, the free-escape boundary simulations without focusing produce a spectrum in the far downstream region that differs from the focused simulation, because of the lack of adiabatic cooling. Thus, if the model should correctly address also the downstream particle fluxes, it should implement adiabatic cooling explicitly. This could be done analytically utilizing the adiabatic cooling rate for an isotropic particle distribution, if advection is the dominant mode of downstream transport.
5 Conclusions and outlook
In this study, Monte Carlo simulations of coronal particle acceleration and transport at an oblique shock, with a scattering mean free path similar to Bell’s theory, are presented. In our simulations, we take into account adiabatic focusing and pitch angle scattering as a result of magnetic irregularities in the plasma. We compared results from non-focused, focused, and non-focused systems with free-escape boundaries to study whether such a boundary can produce results similar to a model with magnetic focusing included.
The steady-state spectra obtained at the shock from all simulations are qualitatively similar as they agree with the power-law dependence predicted by DSA theory with a cutoff that is controlled by focusing (focused simulations) or the location of the free-escape boundary (non-focused simulations). In the presence of focusing, the cutoff momentum in the spectrum achieves a steady-state value, so the maximum achieved energy of the system cannot increase indefinitely as in the non-focused system. The systems with a free-escape boundary also stabilize, but, due to the absence of adiabatic cooling, the energy spectrum in the far downstream is harder than in the focused case.
From the simulation results, it can be observed that a single location of the free-escape boundary condition does not closely match the focused case results of different quantities. The values of α reproducing the focused case are different for the shock spectrum and the escaping spectrum. Therefore, for various systems in space weather modeling scenarios, it is important to carefully identify the location of the free-escape boundary that best reproduces the focusing case.
The theoretical framework of DSA in one dimension was developed without including focusing, but it is clear from our simulations that the effect of focusing on particle transport and acceleration is significant. Thus, adiabatic focusing cannot be completely neglected when simulating the acceleration of SEPs in coronal shocks. However, as demonstrated by our simulations, a carefully positioned upstream free-escape boundary can mimic the particle escape and limit the acceleration rate so that a local model could reproduce the result of a focused transport simulation. This provides justification for space weather models that contain a local self-consistent acceleration region close to the shock coupled with a focused transport simulation in the heliosphere without considering the back-reaction of particles to the Alfvén waves. Because of the very simple coronal and shock model employed in this study, however, more detailed simulation studies are needed to determine, whether (i) a time-dependent shock in a realistic coronal plasma can reach a balance between particle acceleration and losses that could lead to a quasi-stationary state close to the shock and (ii) the values of α are well constrained and can be predicted from the parameters of the shock and the upstream medium close to the shock. Also, particle scattering, here taken to be isotropic, could be modelled closer to the prediction of self-consistent modelling, where the spectral shape of the Alfvén waves yields anisotropic scattering in the quasi-linear approximation (Afanasiev et al., 2015). These improvements will be topics of future studies.
Acknowledgments
We acknowledge the financial support from the European Union’s Horizon 2020 research and innovation programme (EU/H2020) under the Marie Skłodowska-Curie grant agreement No. 955620 (SWATNet). We have received support also from EU/H2020 under grant agreement No. 101004159 (SERPENTINE) and the Academy of Finland, grant No. 336809 (FORESAIL). S.N. acknowledges the financial support of the Finnish Cultural Foundation Varsinais-Suomi Regional Fund. L.V. is grateful for support from the University of Turku Graduate School. N.W. acknowledges support from the Research Foundation – Flanders (FWO-Vlaanderen, fellowship no. 1184319N). S.P. acknowledges support from the projects C14/19/089 (C1 project Internal Funds KU Leuven), G.0B58.23N and G.0025.23N (WEAVE) (FWO-Vlaanderen), 4000134474 (SIDC Data Exploitation, ESA Prodex-12), and Belspo project B2/191/P1/SWiM. The editor thanks two anonymous reviewers for their assistance in evaluating this paper.
References
- Afanasiev A, Battarbee M, Vainio R. 2015. Self-consistent Monte Carlo simulations of proton acceleration in coronal shocks: Effect of anisotropic pitch-angle scattering of particles. A&A 584: A81. https://doi.org/10.1051/0004-6361/201526750. [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Afanasiev A, Vainio R, Trotta D, Nyberg S, Talebpour Sheshvan N, Hietala H, Dresing N. 2023. Self-consistent modeling of the energetic storm particle event of November 10, 2012. A&A 679: A111. https://doi.org/10.1051/0004-6361/202346220. [CrossRef] [EDP Sciences] [Google Scholar]
- Axford WI, Leer E, Skadron G. 1977. The acceleration of cosmic rays by shock waves. In: Proc. of 15th International Cosmic Ray Conference, vol. 11, Plovdiv, Bulgaria, August 13–26, 1977. Bulgarian Academy of Sciences, pp. 132–137. [Google Scholar]
- Bell AR. 1978. The acceleration of cosmic rays in shock fronts – I. Mon Not R Astron Soc 182: 147–156. https://doi.org/10.1093/mnras/182.2.147. [CrossRef] [Google Scholar]
- Berezhko EG, Taneev SN. 2016. Particle acceleration and Alfvén wave generation by an interplanetary shock. Astron Lett 42(2): 126–135. https://doi.org/10.1134/S1063773716010011. [CrossRef] [Google Scholar]
- Bieber JW, Matthaeus WH, Smith CW, Wanner W, Kallenrode M-B, Wibberenz G. 1994. Proton and electron mean free paths: The palmer consensus revisited. A&A 420: 294. https://doi.org/10.1086/173559. [Google Scholar]
- Blandford RD, Ostriker JP. 1978. Particle acceleration by astrophysical shocks. Astrophys J 221: L29–L32. https://doi.org/10.1086/182658. [CrossRef] [Google Scholar]
- Decker RB. 1988. Computer modeling of test particle acceleration at oblique shocks. Space Sci Rev 48(3–4): 195–262. https://doi.org/10.1007/BF00226009. [CrossRef] [Google Scholar]
- Desai M, Giacalone J. 2016. Large gradual solar energetic particle events. Living Rev Sol Phys 13(1): 3. https://doi.org/10.1007/s41116-016-0002-5. [CrossRef] [Google Scholar]
- Ding Z, Li G, Mason G, Poedts S, Kouloumvakos A, Ho G, Wijsen N, Wimmer-Schweingruber RF, Rodríguez-Pacheco J.. 2024. Modelling two energetic storm particle events observed by Solar Orbiter using the combined EUHFORIA and iPATH models. A&A 681: A92. https://doi.org/10.1051/0004-6361/202347506. [CrossRef] [EDP Sciences] [Google Scholar]
- Ding Z, Wijsen N, Li G, Poedts S. 2022. Modeling the 2020 November 29 solar energetic particle event using EUHFORIA and iPATH models. A&A 668: A71. https://doi.org/10.1051/0004-6361/202244732. [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Drury LO. 1983. Review article: An introduction to the theory of diffusive shock acceleration of energetic particles in tenuous plasmas. Rep Prog Phys 46(8): 973–1027. https://doi.org/10.1088/0034-4885/46/8/002. [CrossRef] [Google Scholar]
- Fraschetti F. 2021. Effect of acceleration and escape of energetic particles on spectral steepening at shocks. Astrophys J 909(1): 42. https://doi.org/10.3847/1538-4357/abd699. [CrossRef] [Google Scholar]
- Gordon BE, Lee MA, Möbius E, Trattner KJ. 1999. Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks and Earth’s bow shock revisited. J Geophys Res Space Phys 104(A12): 28263–28278. https://doi.org/10.1029/1999JA900356. [CrossRef] [Google Scholar]
- Hu J, Li G, Ao X, Zank GP, Verkhoglyadova O. 2017. Modeling particle acceleration and transport at a 2-D CME-driven shock. J Geophys Res (Space Phys) 122(11): 10938–10963. https://doi.org/10.1002/2017JA024077. [Google Scholar]
- Kocharov LG, Torsti J, Vainio R, Kovaltsov GA. 1996. Propagation of solar cosmic rays: Diffusion versus focused diffusion. Sol Phys 165(1): 205–208. https://doi.org/10.1007/BF00149100. [CrossRef] [Google Scholar]
- Krymskii GF. 1977. A regular mechanism for the acceleration of charged particles on the front of a shock wave. Akad Nauk SSSR Dokl 234: 1306–1308. [Google Scholar]
- Lee MA. 1983. Coupled hydromagnetic wave excitation and ion acceleration at interplanetary traveling shocks. J Geophys Res Space Phys 88(A8): 6109–6120. https://doi.org/10.1029/JA088iA08p06109. [CrossRef] [Google Scholar]
- Li G, Zank GP, Rice WKM. 2005. Acceleration and transport of heavy ions at coronal mass ejection-driven shocks. J Geophys Res Space Phys 110(A6): A06104. https://doi.org/10.1029/2004JA010600. [Google Scholar]
- Ng CK, Reames DV. 2008. Shock acceleration of solar energetic protons: The first 10 minutes. Astrophys J 686(2): L123. https://doi.org/10.1086/592996. [CrossRef] [Google Scholar]
- Palmer ID. 1982. Transport coefficients of low-energy cosmic rays in interplanetary space. Rev Geophys Space Phys 20: 335–351. https://doi.org/10.1029/RG020i002p00335. [CrossRef] [Google Scholar]
- Reames DV. 2023. How do shock waves define the space-time structure of gradual solar energetic particle events?. Space Sci Rev 219(1): 14. https://doi.org/10.1007/s11214-023-00959-x. [CrossRef] [Google Scholar]
- Rice WKM, Zank GP, Li G. 2003. Particle acceleration and coronal mass ejection driven shocks: Shocks of arbitrary strength. J Geophys Res (Space Phys) 108(A10): 1369. https://doi.org/10.1029/2002JA009756. [Google Scholar]
- Roelof EC. 1969. Propagation of solar cosmic rays in the interplanetary magnetic field. In: Lectures in High-Energy Astrophysics, Ögelman H, Wayland JR (Eds.), Scientific and Technical Information Division, Office of Technology Utilization, NASA, Washington, DC, p. 111. [Google Scholar]
- Ruffolo D. 1995. Effect of adiabatic deceleration on the focused transport of solar cosmic rays. Astrophys J 442: 861. https://doi.org/10.1086/175489. [CrossRef] [Google Scholar]
- Vainio R. 2006. Acceleration of SEPs: Role of CME-associated shocks and turbulence. In: Washington DC American Geophysical Union Geophysical Monograph Series, vol. 165, pp. 253–262. https://doi.org/10.1029/165GM24. [Google Scholar]
- Vainio R, Desorgher L, Heynderickx D, Storini M, Flückiger E, et al. 2009. Dynamics of the Earth’s particle radiation environment. Space Sci Rev 147(3–4): 187–231. https://doi.org/10.1007/s11214-009-9496-7. [CrossRef] [Google Scholar]
- Vainio R, Kocharov L, Laitinen T. 2000. Interplanetary and interacting protons accelerated in a parallel shock wave. Astrophys J 528(2): 1015–1025. https://doi.org/10.1086/308202. [CrossRef] [Google Scholar]
- Vainio R, Laitinen T. 2007. Monte Carlo simulations of coronal diffusive shock acceleration in self-generated turbulence. Astrophys J 658(1): 622–630. https://doi.org/10.1086/510284. [CrossRef] [Google Scholar]
- Vainio R, Pönni A, Battarbee M, Koskinen HEJ, Afanasiev A, Laitinen T. 2014. A semi-analytical foreshock model for energetic storm particle events inside 1 AU. J Space Weather Space Clim 4: A08. https://doi.org/10.1051/swsc/2014005. [CrossRef] [EDP Sciences] [Google Scholar]
- Wijsen N, Aran A, Scolini C, Lario D, Afanasiev A, Vainio R, Sanahuja B, Pomoell J, Poedts S. 2022. Observation-based modelling of the energetic storm particle event of 14 July 2012. A&A 659: A187. https://doi.org/10.1051/0004-6361/202142698. [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Wijsen N, Lario D, Sánchez-Cano B, Jebaraj IC, Dresing N, et al. 2023. The effect of the ambient solar wind medium on a CME-driven shock and the associated gradual solar energetic particle event. Astrophys J 950(2): 172. https://doi.org/10.3847/1538-4357/acd1ed. [CrossRef] [Google Scholar]
Cite this article as: Annie John L, Nyberg S, Vuorinen L, Vainio R, Afanasiev A, et al. 2024. Effects of adiabatic focusing and free-escape boundaries in coronal shock acceleration. J. Space Weather Space Clim. 14, 15. https://doi.org/10.1051/swsc/2024012.
All Figures
 |
Figure 1 Depiction of the one-dimensional simulation geometry, where an oblique shock propagates along a diverging magnetic field B away from the solar surface with a shock obliquity θBn and speed Vs along the modeled magnetic field line. The model is simulated along z (origin at the solar surface) and the magnetic field strength depends on it by B(z) = B0e−z/L. Z is measured along z, but Z = 0 is fixed at the shock. |
| In the text | |
 |
Figure 2 Particle distributions at different times in simulations without focusing (left column), with focusing (middle column), and with a free-escape boundary in the upstream at Z = αL, α = 1 (right column) for an oblique shock propagating outwards from the Sun along an exponentially decreasing magnetic field. The horizontal dotted lines give the injection momentum, and the dashed line in panel (h) gives a characteristic curve for an advecting downstream population undergoing adiabatic cooling. The horizontal stripes in the distributions result from the consecutive interactions of the initially mono-energetic particles with the shock. |
| In the text | |
 |
Figure 3 The cutoff energies (see text for details) of the particles as a function of simulation time for no focusing, focusing, and different free-escape boundary simulation cases close to the shock in the downstream region (−0.05 R⊙ < Z < 0). The location of the free-escape boundary in the upstream of the shock is given by Z = αL, where L = R⊙. |
| In the text | |
 |
Figure 4 The momentum distributions of the particles in downstream close to the shock (−0.05 R⊙ < Z < 0) for no focusing, focusing, and different free-escape boundary simulation cases at a given simulation time, where the focusing and free-escape boundary cases have reached a steady state. The grey dashed line is the canonical power-law of the steady-state DSA theory and the dotted curve on the no-focusing distribution represents the product of the power-law spectrum with the exponential cut-off in energy, exp(−E/Ec). |
| In the text | |
 |
Figure 5 The momentum distributions of the escaping particles in the focusing and free-escape boundary simulations at different points in simulation time. In the focusing simulation, a particle will unlikely return to the shock from Z > L, so particles beyond L upstream will be considered for the momentum distributions of escaped particles. In the free-escape boundary simulations, particles that are beyond the free-escape boundary specified by Z = αL (where L = R⊙) are considered for the momentum distributions of escaped particles. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.