| Issue |
J. Space Weather Space Clim.
Volume 7, 2017
Space weather effects on GNSS and their mitigation
|
|
|---|---|---|
| Article Number | A26 | |
| Number of page(s) | 14 | |
| DOI | https://doi.org/10.1051/swsc/2017020 | |
| Published online | 24 October 2017 | |
Research Article
Multi-frequency GNSS robust carrier tracking for ionospheric scintillation mitigation
1
Centre Tecnològic de Telecomunicacions de Catalunya (CTTC/CERCA),
Barcelona, Spain
2
Department of Electrical and Computer Eng., Northeastern University,
Boston,
MA
02115, USA
3
European Space Agency (ESA),
Noordwijk,
The Netherlands
* Corresponding author: jvila@cttc.cat
Received:
11
May
2017
Accepted:
14
August
2017
Ionospheric scintillation is the physical phenomena affecting radio waves propagating from the space through the ionosphere to earth. The signal distortion induced by scintillation can pose a major threat to some GNSS application. Scintillation is one of the more challenging propagation scenarios, particularly affecting high-precision GNSS receivers which require high quality carrier phase measurements; and safety critical applications which have strict accuracy, availability and integrity requirements. Under ionospheric scintillation conditions, GNSS signals are affected by fast amplitude and phase variations, which can compromise the receiver synchronization. To take into account the underlying correlation among different frequency bands, we propose a new multivariate autoregressive model (MAR) for the multi-frequency ionospheric scintillation process. Multi-frequency GNSS observations and the scintillation MAR are modeled in state-space, allowing independent tracking of both line-of-sight phase variations and complex gain scintillation components. The resulting joint synchronization and scintillation mitigation problem is solved using a robust nonlinear Kalman filter, validated using real multi-frequency scintillation data with encouraging results.
Key words: GNSS / ionospheric scintillation / multivariate AR modeling / robust tracking / carrier phase synchronization / adaptive nonlinear Kalman filter
© J. Vilà-Valls et al., Published by EDP Sciences 2017
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Global Navigation Satellite Systems (GNSS) is the technology of choice for most position-related applications when it is available (Dardari et al., 2015). A GNSS receiver relies on a constellation of satellites to estimate a set of range measures from which to compute its position. The main challenges of GNSS technology arise when operating in complex, harsh propagation scenarios which are naturally impaired by multipath, shadowing, high dynamics, or ionospheric scintillation. In the last decade, ushered by an ever increasing demand for availability, accuracy, and reliability, the mitigation of these challenges has steered intense research on advanced receiver design (Amin et al., 2016).
Among these challenges, in this paper we focus on ionospheric scintillation. Because such disturbance is not related to the local environment, as in the case of multipath or shadowing, it can degrade receiver performance even under ideal open-sky conditions. Ionospheric scintillation is caused by a disturbance in the portion of the ionosphere through which the GNSS signals propagates, an effect particularly relevant in polar and equatorial regions. It can produce rapidly varying constructive and destructive interference between multiple scattered signals. This turbulent behavior can render the carrier phase difficult to track by the receiver. One of the major challenges of severe scintillation propagation conditions is known as canonical fading, which is characterized by a combination of strong fading and rapid phase changes in a simultaneous and random manner (Kintner et al., 2009; Humphreys et al., 2009). From a synchronization standpoint, measuring the signal phase during such a fade is very challenging because rate of change of phase changes is at its highest when the signal amplitude is near its lowest (Humphreys et al., 2005). This may lead the receiver to momentarily lose carrier synchronization, resulting in either cycle-slips or loss of lock. Unfortunately, the accuracy improvement of modern high-precision receivers is based on the use of carrier phase-based positioning techniques, and so it is extremely sensitive to scintillation perturbations (Jacobsen & Dähnn, 2014; Prikryl et al., 2014; Banville & Langley, 2013, Banville et al., 2010).
Traditional synchronization relies on well-known closed-loop DLL/PLL architectures (Kaplan, 2006). However, receiver architectures based on DLL/PLL are not always able to provide continuous and reliable phase tracking (Humphreys et al., 2005). Most of state-of-the-art (SoTA) techniques propose methods to robustify DLL/PLL schemes via fine tuning and augmentation (Yu et al., 2006; López-Salcedo et al., 2014), either by using adaptive bandwidth schemes (Skone et al., 2005) or combined architectures (Chiou, 2010; Won, 2014). It has already been shown that Kalman filter (KF)-based solutions provide better performances and robustness in these situations (Humphreys et al., 2005; Macabiau et al., 2012), being nowadays the performance benchmark for the development of new methodologies (Vilà-Valls et al., 2017b). The natural extension is to use adaptive KF-based solutions (Zhang et al., 2010; Won et al., 2012), which aim at sequentially adapt the filter parameters. However, even these advanced techniques do not solve the estimation versus mitigation trade-off (Vilà-Valls et al., 2015b), because the filter is not able to decouple the different phase contributions (i.e., dynamics and scintillation), and so may provide poor scintillation mitigation capabilities. A scalar tracking approach to overcome these limitations was proposed in Vilà-Valls et al. (2015a,b), where the scintillation physical phenomena is statistically modeled using autoregressive (AR) processes and embedded in the filter formulation. This approach was shown to outperform the SoTA techniques using synthetic data, being effectively able to discriminate between dynamic and scintillation contributions to the estimated carrier-phase. The Cornell Scintillation Model (CSM) (Humphreys et al., 2009, 2010), a popular synthetic signal simulator that generates scintillation amplitude and phase traces, was used to test the AR-based filtering methodology. Recent studies of real equatorial and high-latitude data have shown that scintillation characteristics are frequency-dependent (Carrano et al., 2012; Sokolova et al., 2015; Jiao et al., 2016). While phase disturbances may be correlated, deep amplitude fades tend to occur at different times on different frequencies, thus motivating the potential performance gain of using inter-frequency aiding and multi-frequency architectures.
This paper exploits the statistical relationships between scintillation at different frequency bands to propose a multi-frequency carrier tracking method that virtually mitigates scintillation component. The paper extends our previous work on single-frequency carrier tracking loops under scintillation conditions (Vilà-Valls et al., 2015a,b), for which a state-space formulation and a Kalman filter (KF) was considered. Here, an augmented state-space formulation considering multiple frequencies is investigated and a tracking method proposed on the top of it. Remarkably, the resulting method is validated with real data measurements showing notable performance.
To summarize, in this article, we further explore the idea and preliminary results in Vilà-Valls et al. (2017a) with the following four main contributions:
-
multivariate AR ionospheric amplitude and phase scintillation modeling, featuring a joint fitting of the multi-frequency scintillation time series. An optimal model order selection based on the Bayesian Information Criterion is used. This is discussed in Section 3;
-
the novel multi-frequency joint carrier phase and scintillation state-space model (SSM) formulation, that takes into account the potential correlation at different frequency bands is introduced in Section 4;
-
the proposed robust filter that performs state estimation on the aforementioned SSM is discussed in Section 5. The solution is based on a nonlinear, adaptive KF formulation;
-
as opposed to previous works where synthetic data was used, the proposed method is analyzed using real ionospheric scintillation data in Section 6.
2 Ionospheric scintillation
Scintillation is caused by local variations in the structure of the ionospheric electron density along line-of-sight between the satellite and the receiver. The receiver observes signals that are refracted and diffracted such that the phase and amplitude of the signal exhibits large stochastic perturbations. The severity of the scintillation is traditionally quantified by two indices: an amplitude scintillation index, denoted S4; and a phase scintillation index, denoted σϕ. The indices are computed on a per-signal basis and indicate average intensity of the signal variations over the preceding minute. They have been used for some decades and as a result there exist rich databases of historical data for a wide range of observation points.
Unfortunately these indices offer no insight into the time-correlatedness of the instantaneous phase and amplitude of scintillation observed on multiple frequencies. A number of recent studies have provided empirical evidence that the phase scintillation exhibits a high degree of correlation between different GNSS frequencies, including L1, L2 and L5. It has been suggested that this correlation persists except in the case of strong amplitude scintillation, when deep amplitude fades occur (Sokolova et al., 2015; Carrano et al., 2012; Jiao et al., 2016). This implies that even when strong phase scintillation is observed, which is not uncommon at high latitudes, these variations in the carrier will be correlated across frequencies. When a receiver observes both amplitude and phase scintillation, then it has been observed that the phase variations are correlated depending on the scintillation intensity, but become decorrelated once deep amplitude fades begin to occur (Sokolova et al., 2015). These deep amplitude fades, it has been shown, tend to be uncorrelated across frequencies (Carrano et al., 2012).
From a carrier tracking perspective, these two observations can be exploited to improve and robustify carrier phase tracking. Firstly, the fact that the phase variations are highly correlated implies that a centralized, or joint tracking of the carrier across multiple GNSS frequencies can improve tracking accuracy (Sokolova et al., 2015). Secondly, the fact that deep amplitude fades occur at different times on different frequencies, implies that it is highly unlikely that a receiver will loose lock on multiple frequencies simultaneously, suggesting that it should be possible to assist one frequency with another (Sokolova et al., 2015; Carrano et al., 2012). These concepts are explored in the work presented here.
The experimental work presented in this manuscript, was conducted on data obtained from the Joint Research Centre (JRC) Scintillation Repository a collection of data with more than 10 hours of scintillation events recorded over Hanoi in March and April, 2015 (Curran et al., 2015b). These datasets were based on a reconfigurable quad-channel front-end, Fourtune, which had been programmed to collect triple-frequency data, L1, L2 and L5, using 1-bit complex sampling at rates of 5 MHz, 5 MHz, and 30 MHz, respectively (Curran et al., 2015b). The recording system was configured to continuously record 50-minute datasets and to post-process each using an L1 software defined receiver for the purposes of basic scintillation detection. Those datasets in which severe scintillation was identified were then archived for post-processing, and the others discarded (Curran et al., 2015a).
The post-processing stage employed a multi-frequency open-loop software receiver which exploited precise knowledge of the receiver location, and the well-disciplined reference oscillator to generate accurate reference carrier and code local replicas (Curran et al., 2015b). Once demodulated to complex baseband, the correlator values corresponding to each observed GNSS signal were processed to estimate the phase and amplitude perturbations induced by ionospheric activity. Being an open-loop post-processing scheme, a batch estimation of the amplitude and phase was possible, providing highly accurate and reliable characterization (Curran et al., 2015b). From these 1 kHz estimates ofcarrier phase and amplitude, traditional measures of scintillation activity were computed, such as S4 and σϕ.
Figure 1 shows an example of real equatorial ionospheric scintillation amplitude data for a scintillation event at three different GPS frequency bands on one particular satellite. This is an example of strong scintillation, exhibiting a few fades below –30 dB, and many prolonged fades below –10 dB.
 |
Fig. 1 An example of 100 s of real equatorial scintillation amplitude data for a severe scintillation event at three different GPS frequency bands. |
3 Multivariate AR scintillation signal model
Ionospheric scintillation can be modeled as a multiplicative channel ξs(t), with the received base-band signal being
 (1)
where ρs (t) and θs (t) are the ionospheric scintillation envelope and phase components, respectively; s (t) is the baseband equivalent of the transmitted signal; and w(t) is a randomnoise term including both thermal noise and any other disturbance. The amplitude scintillation strength is typically described by the scintillation index S4, and is usually considered within three main regions (Humphreys et al., 2009): weak, moderate and severe,
(1)
where ρs (t) and θs (t) are the ionospheric scintillation envelope and phase components, respectively; s (t) is the baseband equivalent of the transmitted signal; and w(t) is a randomnoise term including both thermal noise and any other disturbance. The amplitude scintillation strength is typically described by the scintillation index S4, and is usually considered within three main regions (Humphreys et al., 2009): weak, moderate and severe,
 (2)
(2)
It was shown in Vilà-Valls et al. (2013, 2015a,b) for the single-frequency case that both scintillation components can be well approximated using an autoregressive (AR) process. The scalar AR scintillation model is given by
 (3)
(3)
 (4)
with κ a constant value, and the mean of the amplitude scintillation process equal to
(4)
with κ a constant value, and the mean of the amplitude scintillation process equal to  ; {γi, βi} are the set of AR coefficients, and {
; {γi, βi} are the set of AR coefficients, and { ,
, } the driving noise variances. In Vilà-Valls et al. (2017a), we considered this scalar AR approximation to build a multi-frequency SSM, where the model order selection and AR parameters were obtained from synthetic scintillation data. Using this scalar approximation in a multi-frequency scenario is a simplistic approach, because it does not take into account the possible correlations among frequencies, and therefore loses the characteristics of the physical phenomena (see Section 2). To overcome the limitations of the scalar AR processes model in this context, we propose a new multivariate AR (MAR) ionospheric scintillation formulation. Real ionospheric scintillation data was used, selecting the model order and parameters.
} the driving noise variances. In Vilà-Valls et al. (2017a), we considered this scalar AR approximation to build a multi-frequency SSM, where the model order selection and AR parameters were obtained from synthetic scintillation data. Using this scalar approximation in a multi-frequency scenario is a simplistic approach, because it does not take into account the possible correlations among frequencies, and therefore loses the characteristics of the physical phenomena (see Section 2). To overcome the limitations of the scalar AR processes model in this context, we propose a new multivariate AR (MAR) ionospheric scintillation formulation. Real ionospheric scintillation data was used, selecting the model order and parameters.
 (5)
where p is the model order; zk = [zk,1, … , zk,d] ⊤ is the kth sample of a d-dimensional time-series; A1 to Ap ∈ Rd×d are the coefficient matrices of the MAR model; the random vector term ek = [ek,1, … , ek,d] ⊤ is a zero-mean Gaussian random variable with covariance matrix Σe ∈ Rd×d. ek is assumed uncorrelated in time (i.e., E {ekeℓ} = 0 for k ≠ ℓ), but possibly correlated among time-series (i.e., Σe can containoff-diagonal elements); w ∈ Rd is a parameter vector of intercept terms to allow a nonzero mean time-series, which implies an expected value of
(5)
where p is the model order; zk = [zk,1, … , zk,d] ⊤ is the kth sample of a d-dimensional time-series; A1 to Ap ∈ Rd×d are the coefficient matrices of the MAR model; the random vector term ek = [ek,1, … , ek,d] ⊤ is a zero-mean Gaussian random variable with covariance matrix Σe ∈ Rd×d. ek is assumed uncorrelated in time (i.e., E {ekeℓ} = 0 for k ≠ ℓ), but possibly correlated among time-series (i.e., Σe can containoff-diagonal elements); w ∈ Rd is a parameter vector of intercept terms to allow a nonzero mean time-series, which implies an expected value of
 (6)
(6)
The two main MAR modelling challenges are: (i) selectionthe correct model order selection p, and (ii) the time-series analysis to obtain an estimate of the MAR model parameters, 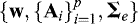 . Both points are discussed in the remainder of this section.
. Both points are discussed in the remainder of this section.
3.1 MAR model order selection
In the statistical and signal processing literature, the Akaike Information Criterion (AIC) (Akaike, 1974), extensions of the AIC such as the corrected AIC (AICc) and the generalized information criterion (GIC), and the Bayesian Information Criterion (BIC) (Schwarz, 1978), are widely used metrics for model order selection. The latter has become the method of choice mainly because: i) while the AIC has a nonzero overfitting probability, this tends to zero in the BIC when the sample size grows, and ii) it is an asymptotic approximation of the optimal maximum a posteriori (MAP) rule (Stoica and Selen, 2004). In this contribution we use the BIC as the model order selection criterion.
In this subsection we define the quantities for a generic time-series composed of N samples, y ∈ RN, and assume θ is the vector parameters of the model with order p, which we aim to select.
(BIC) The Bayesian Information Criterion is defined as (Stoica and Selen 2004)
 (7)
with y being the available data, θ the parameter vector (whose dimension can vary with the model order) and p corresponds to the model order. pp (y, θ) is the likelihood function which depends on the parameter vector θ and the model order p, and the maximum likelihood estimate of the parameters is given by
(7)
with y being the available data, θ the parameter vector (whose dimension can vary with the model order) and p corresponds to the model order. pp (y, θ) is the likelihood function which depends on the parameter vector θ and the model order p, and the maximum likelihood estimate of the parameters is given by  The BIC rule selects the order p that maximizes (7).
The BIC rule selects the order p that maximizes (7).
Definition 2 corresponds to the BIC when a single time-series is fitted. We are, however, interested in jointly fitting multiple time-series (from the various frequencies). This concept is generalized in Definition 3.
(Multivariate BIC) The Bayesian Information Criterion for the multiavariate AR model MAR(p) in Definition 1 yields to a model order estimate according to Neumaier and Schneider (2001)
 (8)
where
(8)
where  and
and  is an estimate of the noise covariance matrix obtained from the N samples.
is an estimate of the noise covariance matrix obtained from the N samples.
The estimates of the noise covariance matrix  are typically obtained for a range of model order values, pmin ≤ p ≤ pmax. An efficient iterative way to compute an estimate of
are typically obtained for a range of model order values, pmin ≤ p ≤ pmax. An efficient iterative way to compute an estimate of  using a QR factorization and a stepwise downdating strategy is shown in Neumaier and Schneider (2001).
using a QR factorization and a stepwise downdating strategy is shown in Neumaier and Schneider (2001).
3.2 MAR model parameters
Several MAR model parameters estimation methods based on the minimization of the prediction error are available in the literature. A thorough comparison of the most common estimators is available in Schlögl (2006). The main conclusion is that when enough samples are available (i.e., N ≥ 400), the performance of the different methods is similar. In this contribution we propose to use the stepwise least squares estimation method proposed in Neumaier and Schneider (2001), which is available as a MatlabTM package named ARfit (Schneider & Neumaier, 2001). This method first rewrites the MAR model as a regression model, and then obtains the parameters using a least squares method.
3.3 Ionospheric scintillation MAR formulation
The MAR multi-frequency ionospheric scintillation model considering M frequency bands (i.e., B1 to BM) is given by
 (9)
(9)
 (10)
where
(10)
where  ,
,  , and the ensemble of q + p + 3 MAR model parameters is given by
, and the ensemble of q + p + 3 MAR model parameters is given by  . Notice that each of these matrices has dimension M × M, given by the number of frequency bands. It is worth saying that the MAR model noise covariance matrices, Σρ and Σθ, provide a good indicator of the inter-frequency correlation of the time-series. It has been found empirically from the estimated noise covariances that while Σρ is almost diagonal (i.e., no correlation in the ionospheric scintillation amplitude), significant values off the main diagonal appear in Σθ (i.e., higher inter-frequency correlation in the ionospheric scintillation phase).
. Notice that each of these matrices has dimension M × M, given by the number of frequency bands. It is worth saying that the MAR model noise covariance matrices, Σρ and Σθ, provide a good indicator of the inter-frequency correlation of the time-series. It has been found empirically from the estimated noise covariances that while Σρ is almost diagonal (i.e., no correlation in the ionospheric scintillation amplitude), significant values off the main diagonal appear in Σθ (i.e., higher inter-frequency correlation in the ionospheric scintillation phase).
A key point to exploit the MAR scintillation approximation within a filtering framework is the model order selection. In Vilà-Valls et al. (2013, 2015a,b), the selection was done inspecting the power spectral densities (PSD), and subsequently in Vilà-Valls et al. (2017a), we used a statistical test based on the partial autocorrelation functions (PAF). Both analyses were done using synthetic data. In this contribution we use the BIC in Definition 3 and perform the fitting on real multi-frequency scintillation data.
Figure 2 shows the C∕N0 (carrier-to-noise density ratio) and amplitude scintillation index estimations, S4, at three different GPS frequency bands (i.e., L1, L2, and L5). These results correspond to two ionospheric scintillation events recorded over Hanoi in March and April 2015 (cf. Sect. 2). While the first event (top figure) corresponds to a moderate to low scintillation scenario, the second one (bottom figure) is clearly a strong scintillation case. Thus, the real data available (over 3 hours of equatorial scintillation) contains both low, moderate and severe scintillation scenarios.
To obtain the model order for both amplitude and phase scintillation processes, we processed over 4 hours of 3-dimensional time-series to compute the BIC metrics in (8). BIC results are obtained from non-overlapped sequences of N = 500 samples (5 s). In contrast to the single-frequency fitting to synthetic data given in Vilà-Valls et al. (2013, 2015a,b), the conclusion from the MAR analysis is that a suitable model order to fit the majority of scintillation scenarios is given by q = 6 and p = 5, i.e. a MAR(6) and MAR(5) for the scintillation amplitude and phase, respectively. These results are in contrast to the analysis of previous contributions (based on synthetic data), where lowerorders were sufficient. To justify the choice of the model order, we plot in Figure 3 the histograms of the order selection obtained from real multi-frequency ionospheric scintillation data.
 |
Fig. 2 C∕N0 and S4 scintillation index estimation at three GPS frequency bands for two ionospheric scintillation events recorded over Hanoi in March and April 2015. |
 |
Fig. 3 Empirical model order probability density functions obtained from real multi-frequency ionospheric scintillation data. |
4 Multi-frequency GNSS and ionospheric scintillation state-space model
4.1 Single frequency GNSS signal model
The generic GNSS baseband transmitted signal is given by
 (11)
with Px (t) the received power, d(t) the navigation message and c(t) the spreading code, τ(t) the code delay and θ(t) = 2πfd(t) + θe(t) the carrier phase, where fd(t) is the carrier Doppler frequency shift and θe (t) a carrier phase term including other phase impairments. After the acquisition stage, the samples at the output of the correlators are (Spilker, 1996)
(11)
with Px (t) the received power, d(t) the navigation message and c(t) the spreading code, τ(t) the code delay and θ(t) = 2πfd(t) + θe(t) the carrier phase, where fd(t) is the carrier Doppler frequency shift and θe (t) a carrier phase term including other phase impairments. After the acquisition stage, the samples at the output of the correlators are (Spilker, 1996)
 where Ts is the sampling rate, k stands for the discrete time tk = kTs, Ak is the signal amplitude at the output of the correlators, dk is the data bit, R(⋅) is the code autocorrelation function and
where Ts is the sampling rate, k stands for the discrete time tk = kTs, Ak is the signal amplitude at the output of the correlators, dk is the data bit, R(⋅) is the code autocorrelation function and  are, respectively, the code delay, Doppler shift and carrier phase errors. Focusing on carrier-tracking, we work under the assumption of perfect timing synchronization and data wipe-off, resulting in a signal model
are, respectively, the code delay, Doppler shift and carrier phase errors. Focusing on carrier-tracking, we work under the assumption of perfect timing synchronization and data wipe-off, resulting in a signal model
 (12)where amplitude αk and phase θk may include any non-nominal harsh propagation disturbance. For instance, including the ionospheric scintillation into the signal model leads to αk = Akρs,k and θk = θd,k + θs,k. The dynamics phase term θd,k refers to the line-of-sight (LOS) phase evolution due to the relative movement between the satellite and the receiver.
(12)where amplitude αk and phase θk may include any non-nominal harsh propagation disturbance. For instance, including the ionospheric scintillation into the signal model leads to αk = Akρs,k and θk = θd,k + θs,k. The dynamics phase term θd,k refers to the line-of-sight (LOS) phase evolution due to the relative movement between the satellite and the receiver.
Standard carrier tracking architectures, being proportional plus integral controller in the form of a PLL, model θd,k using a Taylor approximation of the time-varying phase evolution according to the expected dynamics. Typically, a 3rd order representation of the dynamics phase evolution is considered
 (13)
where θ0 (rad) is a random phase value, fd,k (Hz) the carrier Doppler frequency, and fr,k (Hz/s) the Doppler frequency rate.
(13)
where θ0 (rad) is a random phase value, fd,k (Hz) the carrier Doppler frequency, and fr,k (Hz/s) the Doppler frequency rate.
4.2 Multi-frequency GNSS state-space model
In a multi-frequency architecture, a single satellite transmits simultaneously at different frequencies, therefore at the receiver side several measurements are available. Although the methodology in this paper is general for any GNSS signal, we focus on a modern GPS triple band satellite, which transmits on the L1, L2 and L5 frequencies. In this case, the measurements are given by
 (14)
which may be useful to rewrite in real form as
(14)
which may be useful to rewrite in real form as
 (15)where for each frequency, yk = yi,k + iyq,k, θk = θd,k + θs,k and nk = ni,k + jnq,k.
(15)where for each frequency, yk = yi,k + iyq,k, θk = θd,k + θs,k and nk = ni,k + jnq,k.
The different LOS carrier-phase evolutions, when referencing all of the dynamics to L1, are given by
 (16)
with
(16)
with  ,
,  and
and  being the carrier frequencies at the different bands. It is important to notice that the same Doppler frequency terms, fd,k and fr,k, appear in both frequencies. The multi-frequency noise diagonal covariance matrix is
being the carrier frequencies at the different bands. It is important to notice that the same Doppler frequency terms, fd,k and fr,k, appear in both frequencies. The multi-frequency noise diagonal covariance matrix is

In general, xk refers to the state to be tracked and is defined as  with dimension nx = 5 + 3q + 3p and
with dimension nx = 5 + 3q + 3p and
 (17)
(17)
 (18)
(18)
 (19)
(19)
The LOS dynamic carrier-phase state evolution
 (20)
where
(20)
where  ,
,  and
and  stands for possible uncertainties or mismatches on the dynamic model. The covariance Qd,k is usually a priori fixed according to the problem under consideration.
stands for possible uncertainties or mismatches on the dynamic model. The covariance Qd,k is usually a priori fixed according to the problem under consideration.
From the MAR scintillation model in (9), the multi-frequency scintillation amplitude state evolution is
 (21)
where the elements not specified are 0, IM refers to the identity matrix of dimension M × M,
(21)
where the elements not specified are 0, IM refers to the identity matrix of dimension M × M,  with block diagonal covariance matrix Qρ,k = blkdiag (Σρ, 0M(q-1)×M(q-1)) and κρ is a null vector except for the first M values given by κ. Equivalently, we define the scintillation phase state evolution from (10) as
with block diagonal covariance matrix Qρ,k = blkdiag (Σρ, 0M(q-1)×M(q-1)) and κρ is a null vector except for the first M values given by κ. Equivalently, we define the scintillation phase state evolution from (10) as
 (22)with
(22)with  and block diagonal covariance matrix Qθ,k = blkdiag (Σθ, 0M(p-1)×M(p-1)). Finally, the complete state evolution equation reads,
and block diagonal covariance matrix Qθ,k = blkdiag (Σθ, 0M(p-1)×M(p-1)). Finally, the complete state evolution equation reads,
 (23)where the Gaussian process noise has a block diagonal covariance matrix Qk = blkdiag(Qd,k, Qρ,k, Qθ,k). Equations (15) and (23) define the new SSM formulation. Notice that in contrast to the SSM in Vilà-Valls et al. (2017a), in this case the possible correlation between scintillation amplitude and phase at different frequency bands is accounted for.
(23)where the Gaussian process noise has a block diagonal covariance matrix Qk = blkdiag(Qd,k, Qρ,k, Qθ,k). Equations (15) and (23) define the new SSM formulation. Notice that in contrast to the SSM in Vilà-Valls et al. (2017a), in this case the possible correlation between scintillation amplitude and phase at different frequency bands is accounted for.
5 New robust filtering methodology
In this article we elaborate on the previous KF-based architecture proposed in Vilà-Valls et al. (2017a), and extended in Section 4, where the scintillation physical phenomena is mathematically modeled and embedded into the state-space formulation. A nonlinear extended KF (EKF) formulation allows to directly operate with the received signal samples, avoiding the problems associated to the use of a phase discriminator, that is, nonlinearities, loss of Gaussianity and possible saturation at low C ∕ N0. Using the SSM in (15) and (23), and the MAR formulation in Section 3.3, recall that the main parameters of the filter are


 which mainly depend on the amplitude MAR(6) and phase MAR(5) set of parameters obtained from fitting to real multi-frequency data, ***. The complete state x k (nx = 38) to be tracked is defined in equation (25), Qd,k is a priori fixed by the user from the expected dynamics, and the measurement noise variances (i.e.,
which mainly depend on the amplitude MAR(6) and phase MAR(5) set of parameters obtained from fitting to real multi-frequency data, ***. The complete state x k (nx = 38) to be tracked is defined in equation (25), Qd,k is a priori fixed by the user from the expected dynamics, and the measurement noise variances (i.e.,  ,
,  and
and  ) can be sequentially adjusted from the nominal C ∕ N0 estimators at each frequency band, being available at the receiver.
) can be sequentially adjusted from the nominal C ∕ N0 estimators at each frequency band, being available at the receiver.
The main idea behind the EKF is to linearize the nonlinear measurement function around the predicted state estimate, and then use the standard linear KF equations (Anderson and Moore 1979). In this case, the measurement function is given by
 (24)
and the linearized (Jacobian) measurement matrix to be used in the KF measurement update step is1
(24)
and the linearized (Jacobian) measurement matrix to be used in the KF measurement update step is1
 with the different matrices given in equations (26)–(28). Note that the matrix is evaluated at the predicted state,
with the different matrices given in equations (26)–(28). Note that the matrix is evaluated at the predicted state,  , with
, with  for each frequency2.
for each frequency2.
 (25)
(25)
 (26)
(26)
 (27)
(27)
 (28)
(28)
For the sake of completeness, the EKF formulation of the general carrier-phase tracking problem is sketched in Algorithm 1. Notice that the Kalman gain, Kk, is computed from the possibly time-varying system noise matrices, Qk and Rk, which implies that the filter is adapting its behavior to the actual working conditions and has an implicit adaptive bandwidth, in contrast to the traditional PLL with constant coefficients (i.e., fixed bandwidth) (Vilà-Valls et al. 2017b).
Algorithm 1 Carrier-phase tracking EKF formulation

In practice, we compute an estimate of the MAR parameters using a subset of the real multi-frequency ionospheric scintillation data available. To obtain meaningful results, in the simulations we use a small sample set to obtain the model parameters and process the rest of the scintillation time-series to assess the filter performance. In other words, we test the robustness of the method by decoupling the model fitting from the state tracking. Finally, the block diagram of the new multi-frequency nonlinear EKF-based architecture for efficient scintillation mitigation is sketched in Figure 4. It includes both the state estimation procedure and the update of the prediction/estimation error covariance matrices.
 |
Fig. 4 Block diagram of the new multi-frequency nonlinear EKF-based architecture. |
6 Results and discussion
The performance of the proposed method (named MAR-EKF in the simulations) is analyzed using the real equatorial multi-frequency ionospheric scintillation data described in Section 2. We processed 6 sets of data (i.e., over 4 hours of data), each corresponding to a different scintillation event, containing low, moderate and severe ionospheric scintillation propagation conditions (see Eq. (2)). The different events are described in Table 1, with the corresponding estimation of the scintillation index S4 shown in Figure 5. From the state vector in (25), the parameters of interest are the phase components related to the dynamics of the receiver, i.e., obtaining a good estimate of these parameters directly implies good ionospheric scintillation mitigation capabilities. Therefore, this is the final goal of the new receiver architecture. Note that in some applicationsit may be interesting to obtain an estimate of the scintillation amplitude and phase components, ρs,k and θs,k .
The results obtained with the MAR-EKF are compared to the current state-of-the-art techniques, and the latest contributions using scalar AR scintillation model approximations:
-
3rd order PLL with equivalent bandwidth Bw = 5 Hz.
-
Standard discriminator-based KF-based tracking.
-
Adaptive discriminator-based KF (AKF), adjusting the measurement noise variance from the C∕N0 estimate.
-
The scalar AKF-AR presented in Vilà-Valls et al. (2015b), only tracking thescintillation phase, and using a C∕N0 estimate to tune the measurement noise variance at the output of the discriminator.
-
The scalar AEKF-AR presented in Vilà-Valls et al. (2015a), tracking both scintillation amplitude and phase, treating each frequency separately.
We consider a Doppler profile given by an initial random phase in [- π, π], initial Doppler fd,0 = 50 Hz and rate fr,0 = 100 Hz/s, and a relatively low nominal C ∕ N0 = 30 dB–Hz. The signal is sampled at Ts = 10 ms. The measure of performance is the root mean square error (RMSE) on the carrier-phase of interest, i.e.,  ,
,  and
and  . We define the RMSE (radians) over time for each frequency Lj as
. We define the RMSE (radians) over time for each frequency Lj as
 (29)
which is obtained from long real data sets of Nt samples.
(29)
which is obtained from long real data sets of Nt samples.
The proposed methodology is characterized via an in depth analysis, considering the steady-state performance for several representative scenarios: (i) a low scintillation scenario which is used as an architecture validation, (ii) scintillation mitigation capabilities in challenging moderate and severe scintillation scenarios, (iii) robustness to modeling mismatch, where we take into account possible scintillation under and overestimation, and (iv) the estimation performance for the ionospheric scintillation amplitude and phase components.
Real equatorial multi-frequency ionospheric scintillation data characterization.
 |
Fig. 5 Estimated scintillation index S4 for the 6 sets of real multi-frequency equatorial scintillation data, i.e., #1 (top) to #6 (bottom). |
6.1 Low scintillation scenario: architecture validation
In general, it is held that low ionospheric scintillation conditions are given for S4 < 0.4. From Figure 5, we easily identify these conditions in the scintillation events #1 (t = 1500 -- 2500s), #2 (t = 100 -- 1800s), #3 (t = 100 -- 1700s) and #5 (t = 100 -- 1900s). A desired behavior of any tracking method designed to mitigate moderate and severe scintillation conditions is that it performs at least as good as the standard tracking techniques when low or no scintillation is present. Therefore, analyzing the performance of the proposed MAR-EKF in such scenarios can be understood as a representative architecture validation procedure.
We show the RMSEt (Lj) in radians, obtained for two different low scintillation scenarios (500s of data), in Table 2. In this case, we can see that the performance obtained with the two EKF-based solutions, i.e., AEKF-AR and MAR-EKF, is similar but slightly better with the MAR-EKF. Moreover, these methods provide a lower RMSE than the one given by the PLL and the three discriminator-based KF solutions, i.e., KF, AKF and AKF-AR. Therefore, we have two main conclusions: i) the proposed architecture is a valid approach even if no scintillation is present in the signal, that is, the filter is robust and including the scintillation components into the state to be tracked does not induce an error on the estimation of the dynamics related phase, and ii) it may be preferable to avoid discriminator-based architectures and operate directly with the received signal samples. Moreover, in this case we can include the scintillation amplitude into the state formulation, thus being aware of possible fading and amplitude variations.
Root mean square phase tracking error considering real scintillation data at different GPS frequency bands for the low scintillation events #3 (t = 200–700s) and #2 (t = 200–700s).
6.2 Assessing the scintillation mitigation capabilities in moderate and severe scintillation scenarios
The main goal of the proposed architecture is to effectively counteract the undesired ionospheric effects in moderate and severe scintillation scenarios, without sacrificing performance in nominal scenarios (cf. Section 6.1). In this section, we analyze the performance of the MAR-EKF under harsh propagation conditions as per Table 1.
6.2.1 Moderate scintillation
For the sake of completeness, we plot an example of the steady-state instantaneous dynamics phase estimation error for the moderate scintillation event #1 (t = 200–600s) at L5, obtained with the AKF-AR, AEKF-AR and the MAR-EKF. Notice that we do not plot the results for the other methods because their performance is significantly poorer (see Table 3 for RMSE results). In view of the results, the benefits of the new multi-frequency approach with respect to the other filters using scalar AR approximations are apparent.
To obtain statistically more representative results, we show the RMSEt (Lj), obtained for events #1 (t = 500 -- 1000s) and #4 (t = 1300 -- 1800s), in Table 3. These results verify the appropriate behavior of the new architecture, indicating that it outperforms the other methods under moderate scintillation conditions. Again, there is a significant performance improvement attained when avoiding the use of a discriminator. Specifically, the performance obtained with the AEKF-AR and MAR-EKF is improved with respect to the othermethods. This is due to the Gaussianity assumption,which is does not hold when working with a discriminator under fading conditions (Vilà-Valls et al. 2017b).
Root mean square phase tracking error considering real scintillation data at different GPS frequency bands for the moderate scintillation events #1 (t = 500–1000s) and #4 (t = 1300–1800s)
 |
Fig. 6 Steady-state instantaneous dynamics phase estimation error for the moderate scintillation event #1 (t = 200–600s) at L5. |
6.2.2 Severe scintillation
Finally, we assess the performance of the MAR-EKF in challenging, severe scintillation conditions. Figure 7 shows an example of the steady-state instantaneous dynamics phase estimation error for the severe scintillation event #6 (t = 1800–2200s) at L2, obtained with the AKF-AR, AEKF-AR and the MAR-EKF. The best estimation performance is given by the MAR-EKF.
The RMSEt (Lj), obtained for events #3 (t = 2000 – 2500s), #4 (t = 2000 – 2500s) and #6 (t = 1700 – 2200s), is shown in Table 4. These results confirm that the new architecture is superior to the rest of tracking methods also under severe scintillation, providing a significant performance improvement with respect to standard approaches and the scalar EKF-based solution in Vilà-Valls et al. (2015a), which justifies the interest and importance of considering a multi-frequency approach. Overall, the MAR-EKF appears to be relatively robust against a wide range scintillation propagation conditions.
 |
Fig. 7 Steady-state instantaneous dynamics phase estimationerror for the severe scintillation event #6 (t = 1800–2200s) at L2. |
Root mean square phase tracking error considering real scintillation data at different GPS frequency bands for the strong scintillation events #3 (t = 2000–2500s), #4 (t = 2000–2500s) and #6 (t = 1700–2200s).
6.3 Robustness to modeling mismatch
To fully characterize the proposed methodology, we analyze the impact of an incorrect MAR model parameters estimation on the filterperformance, that is, fitting the scintillation amplitude MAR(6) and phase MAR(5) to a set of real data with a different scintillation behavior than the actual signal being processed. Two cases are considered: i) underestimation of the scintillation conditions, which implies that while the filter deals with a severe scintillation scenario, the MAR model parameters are fitted to moderate scintillation data; and ii) overestimation of the scintillation conditions, which refers to themoderate scintillation case with MAR model parameters fitted to severe scintillation data.
The RMSEt (Lj), obtained for the severe scintillation event #6 (t = 1700 -- 2200s) considering an underestimated fitting, and for the moderate scintillation event #6 (t = 1300 -- 1700s) with an overestimated fitting, is shown in Table 5. It is interesting to note that the performance degradation when having a model mismatch is reasonably bounded. In practice, it is always desirable to overestimate, rather than underestimate, the scintillation intensity.
Root mean square phase tracking error considering real scintillation data under modeling mismatch for the severe scintillation event #6 (t = 1700–2200s) and the moderate scintillation event #6 (t = 1300–1700s).
6.4 Scintillation amplitude and phase estimation
In this section we analyze the estimation performance for the scintillation amplitude and phase components, ρs,k and θs,k . We define the corresponding RMSE over time for each frequency Lj as
 (30)
(30)
 (31)
which are obtained from Nt data samples. Notice that standard methods track the complete phase of the signal, therefore we do not have an estimate of the scintillation components. The results obtained with the MAR-EKF are compared to the scalar AKF-AR (i.e, only scintillation phase) and AEKF-AR.
(31)
which are obtained from Nt data samples. Notice that standard methods track the complete phase of the signal, therefore we do not have an estimate of the scintillation components. The results obtained with the MAR-EKF are compared to the scalar AKF-AR (i.e, only scintillation phase) and AEKF-AR.
First we plot an example of the scintillation amplitude and phase estimates delivered by the MAR-EKF, for the severe scintillation event #3 at L5, in Figure 8. We can observe a remarkable recovery of scintillation components by the MAR-EKF filter. Both  and
and  are shown in Table 6. Again, we confirm that the MAR-EKF provides the best estimation performance for both scintillation amplitude and phase components. The performance gain with respect to the other methods using scalar AR approximations is clear for the severe scintillation scenario. In the moderate scintillation case, the performance obtained with the AEKF-AR and the MAR-EKF are equivalent.
are shown in Table 6. Again, we confirm that the MAR-EKF provides the best estimation performance for both scintillation amplitude and phase components. The performance gain with respect to the other methods using scalar AR approximations is clear for the severe scintillation scenario. In the moderate scintillation case, the performance obtained with the AEKF-AR and the MAR-EKF are equivalent.
 |
Fig. 8 Scintillation amplitude and phase estimation for the severe scintillation event #3 at L5. |
Root mean square scintillation components trackingerror considering real scintillation data for the moderate scintillation event #1 (t = 500–1000s) and the severe scintillation event #3 (t = 2000–2500s).
6.5 Cycle slip performance analysis
To conclude the characterization of the new methodology, we assess its robustness to cycle slips, which is particularly necessary in carrier-based positioning techniques such as real-time-kinematic (RTK) and precise-point-positioning (PPP) that rely on the integrity of carrier phase measurements.
In terms of cycle slips, the most challenging scenario is the severe scintillation event #6. We can see in Figure 5 that this event has the highest values for the scintillation index S4 . We show the phase error for the different methods in Figure 9. While some cycle slips appear with the discriminator-based PLL, KF, AKF and AKF-AR, the methods including both scintillation components into the SSM formulation, AEKF-AR, MAR-EKF, are more robust (i.e., no cycle slips). These results confirm the enhanced filtering performance of the new approach. Notice that for this particular scenario, the number of cycle slips with the AKF is higher than with the standard PLL and KF. This is because the filter is not able to cope with the strong fadings during severe scintillation due to the fast changes on the estimated C∕N0, which controls the noise variance at the output of the discriminator. This is also the case with the discriminator-based AKF-AR, which does not take into account the scintillation amplitude. The number of cycle slips for event #6 and the three GPS frequency bands is shown in Table 7, which again confirm the superiority in terms of robustness of the new MAR-EKF.
 |
Fig. 9 Phaseerror for event #6, GPS L2. |
Number of cycle slips for the real ionospheric scintillation event #6.
7 Conclusions
Carrier-phase measurements can be severely degraded due to ionospheric scintillation. This paper proposes a new tracking methodology that is able to extract the desired phase component, used for positioning, from the scintillation component. A key point is first to model both ionospheric scintillation components, amplitude and phase, using an AR model formulation, and then include them into the state to be tracked by the filter. This allows to decouple the phase contribution due to the LOS dynamics from the phase perturbations induced by the ionosphere. Particularly, we want to exploit the advantages of multi-frequency architectures, because the scintillation characteristics are frequency-dependent. To take into account possible correlations among frequencies we must resort to multivariateAR models. A new state-space model is introduced and a Kalman-type state estimator operating on the outputs of the correlators implemented. The new method is validated using real scintillation data recorded in Hanoi, March and April 2015. It has been shown that the new filter outperforms state-of-the-art solutions in the tested scenarios, both in terms of mean square error and robustness to cycle slips. This approach provides a solution to the estimation/mitigation challenge when dealing with scintillation corrupted measurements.
One of the main challenges in the design of the proposed solution is the estimation of the multivariate AR model parameters. While in the analysis conducted in this article these parameters have been obtained by fitting the desired model to a small part of the real time-series available (i.e., then processing a different part of the data), in real-life conditions, where the scintillation conditions evolve over time, we should consider an iterative procedure to adapt the filter to the actual working conditions. Another important point is how to fix the LOS phase dynamics covariance matrix, which depends on the expected dynamics. To fully characterize the new method, it would be desirable to have a larger set of data, recorded at different points over the earth, at different latitudes and containing several events. Even if the set of data available is representative of different scintillation conditions, it would be interesting to obtain a statistically more representative analysis.
Acknowledgments
This work has been supported by the Spanish Ministry of Economy and Competitiveness through project TEC2015-69868-C2-2-R (ADVENTURE) and by the Government of Catalonia under Grant 2014–SGR–1567. The editor thanks two anonymous referees for their assistance in evaluating this paper.
References
- Akaike H. 1974. A new look at the statistical identification model. IEEE Trans Automatic Control 19(6): 716–723. [CrossRef] [Google Scholar]
- Amin MG, Closas P, Broumandan A, Volakis JL. 2016. Vulnerabilities, threats, and authentication in satellite-based navigation systems [scanning the issue]. Proc IEEE 104(6): 1169–1173. [CrossRef] [Google Scholar]
- Anderson B, Moore JB. 1979. Optimal filtering. Englewood Cliffs, New Jersey, USA: Prentice-Hall. [Google Scholar]
- Banville S, Langley RB. 2013. Mitigating the impact of ionospheric cycle slips in GNSS observations. J Geodesy 87(2): 179–193 [CrossRef] [Google Scholar]
- Banville S, Langley RB, Saito S, Yoshihara T. 2010. Handling cycle slips in GPS data during ionospheric plasma bubble events. Radio Science 45(6): 1–15, RS6007, DOI:10.1029/2010RS004415. [CrossRef] [EDP Sciences] [Google Scholar]
- Carrano CS, Groves KM, McNeil WJ, Doherty PH. 2012. Scintillation Characteristics across the GPS Frequency Band. In: Proceedings of the 25th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2012), Nashville, TN, USA, September 17–21, pp. 1972–1989. [Google Scholar]
- Chiou T-Y. Design of a Doppler-aided GPS navigation system for weak signals caused by strong ionospheric scintillation, Ph.D. thesis, Stanford, 2010 [Google Scholar]
- Curran JT, Bavaro M, Morrison A, Fortuny J. 2015a. Event identification & recording for scintillation monitoring stations. In: Proceedings ofthe 2015 International Technical Meeting of The Institute of Navigation, Dana Point, CA, USA, January 2015, pp. 114–122. [Google Scholar]
- Curran JT, Bavaro M, Morrison A, Fortuny J. 2015b. Operating a network of multi-frequency software-defined ionosphere monitoring receivers. In: Proc. of the 28th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2015), Tampa, FL, USA, September 14–18, pp. 3469–3479 [Google Scholar]
- Dardari D, Closas P, Djurić PM. 2015. Indoor tracking: Theory, methods, and technologies. IEEE Trans Veh Technol 64(4): 1263–1278. [Google Scholar]
- Humphreys TE, Psiaki ML, Kintner PM. 2010. Modeling the effects of ionospheric scintillation on GPS carrier phase tracking. IEEE Trans Aerosp Electron Syst 46(4): 1624–1637. [CrossRef] [Google Scholar]
- Humphreys TE, et al. 2005. GPS carrier tracking loop performance in the presence of ionospheric scintillations. In: Proc. of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, USA, September 13–16, pp. 156–167. [Google Scholar]
- Humphreys TE, et al. 2009. Simulating ionosphere-induced scintillation for testing GPS receiver phase tracking loops. IEEE J Select Top Signal Process 3(4): 707–715. [Google Scholar]
- Jacobsen KS, Dähnn M. 2014. Statistics of ionospheric disturbances and their correlation with GNSS positioning errors at high latitudes. J Space Weather Space Clim, 4: A27, doi:10.1051/swsc/2014024. [CrossRef] [EDP Sciences] [Google Scholar]
- Jiao Y, Xu D, Morton Y, Rino C. 2016. Equatorial scintillation amplitude fading characteristics across the GPS frequency bands. NAVIGATION J Inst Navig 63(3): 267–281. [CrossRef] [Google Scholar]
- Kaplan ED, ed. 2006. Understanding GPS: principles and applications, 2nd edn. Artech House. [Google Scholar]
- Kintner PM, Humphreys TE, Hinks J. 2009. GNSS and ionospheric scintillation. How to survive the next solar maximum. Inside GNSS 22–33, [Google Scholar]
- López-Salcedo J, Peral-Rosado J, Seco-Granados G. 2014. Survey on robust carrier tracking techniques. IEEE Commun Surv Tutor 16(2): 670–688. [CrossRef] [Google Scholar]
- Macabiau C, et al. 2012. Kalman filter based robust GNSS signal tracking algorithm in presence of ionospheric scintillations. In: Proceedings of the 25th International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2012). Nashville, TN, USA, September 17–21, 3420–3434. [Google Scholar]
- Neumaier A, Schneider T. 2001. Estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Trans Math Softw 27(1): 27–57. [Google Scholar]
- Prikryl P, Jayachandran PT, Mushini SC, Richardson IG. 2014. High-latitude GPS phase scintillation and cycle slips during high-speed solar wind streams and interplanetary coronal mass ejections: a superposed epoch analysis. Earth Planets Space 66(1): 1–10. [Google Scholar]
- Schlögl A. 2006. A comparison of multivariate autoregressive estimators. Signal Process 86: 2426–2429. [CrossRef] [Google Scholar]
- Schneider T, Neumaier A. 2001 Algorithm 808: ARfit – a MATLAB package for the estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Trans Math Softw 27(1): 58–65. [Google Scholar]
- Schwarz G. 1978. Estimating the dimension of a model. Ann Stat 6(2): 461–464. [Google Scholar]
- Skone G, Lachapelle G, Yao D, Yu W, Watson R. 2005. Investigating the impact of ionospheric scintillation using a GPS software receiver. In: Proc. of the 18th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2005), Long Beach, CA, September 13–16, pp. 1126–1137. [Google Scholar]
- Sokolova N, Morrison A, Curran JT. 2015. High latitude phase scintillation decorrelation across GNSS frequencies - exploring the impact of scintillation on multi-frequency users. Eur J Navigat 13(3): 45–51. [Google Scholar]
- Spilker JJ. 1996. Fundamentals of signal tracking theory. In: Parkinson BW, Spilker JJ, eds. Global positioning system: theory and applications, Vol. I. American Institute of Aeronautics and Astronautics, pp. 245–328. [CrossRef] [Google Scholar]
- Stoica P, Selen Y. 2004. Model-order selection: a review of information criterion rules. IEEE Signal Process Mag 21(4): 36–47. [NASA ADS] [CrossRef] [Google Scholar]
- Vilà-Valls J, Closas P, Curran JT. 2017a. Performance analysis of multi-frequency GNSS carrier tracking for strong ionospheric scintillation mitigation. In: Proceedings of the 25th European Signal Processing Conference (EUSIPCO’17), Kos Island, Greece, August 28 to September 2. [Google Scholar]
- Vilà-Valls J, Closas P, Fernández-Prades C. 2015a. Advanced KF-based methods for GNSS carrier tracking and ionospheric scintillation mitigation. In: Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, March 7–14. [Google Scholar]
- Vilà-Valls J, Closas P, Fernández-Prades C, Lopez-Salcedo JA, Seco-Granados G. 2015b. Adaptive GNSS Carrier Tracking under Ionospheric Scintillation: estimation vs mitigation. IEEE Comm Lett 19(6): 961–964. [CrossRef] [Google Scholar]
- Vilà-Valls J, Closas P, Navarro M, Fernández-Prades C. 2017b. Are PLLs dead? a tutorial on kalman filter-based techniques for digital carrier synchronization. IEEE Aerosp Electron Syst Mag. [Google Scholar]
- Vilà-Valls J, Lopez-Salcedo JA, Seco-Granados G. 2013. An interactive multiple model approach for robust GNSS carrier phase tracking under scintillation conditions. In: Proc. IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Vancouver, BC, Canada, May 26–31. [Google Scholar]
- Won JH. 2014. A novel adaptive digital phase-lock-loop for modern digital GNSS receivers. IEEE Comm Lett 18(1): 46–49. [CrossRef] [Google Scholar]
- Won J-H, Eissfeller B, Pany T, Winkel J. 2012. Advancedsignal processing scheme for GNSS receivers under ionospheric scintillation. In: Proceedings of the IEEE/ION Position Location and Navigation Symposium (PLANS), Myrtle Beach, CA, USA, April 23–26, pp. 44–49. [CrossRef] [Google Scholar]
- Yu W, Lachapelle G, Skone S. 2006. PLL performance for signalsin the presence of thermal noise, phase noise, and ionospheric scintillation. In: Proceedings of the 19th International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS 2006), Fort Worth, TX, USA, September 26–29, pp. 1341–1357. [EDP Sciences] [Google Scholar]
- Zhang L, Morton YT, Miller MM. 2010. A variable gain adaptive Kalman filter-based GPS carrier tracking algorithms for ionosphere scintillation signals. In: Proceedings of the 23rd International Technical Meeting of The Satellite Division of the Institute of Navigation (ION GNSS 2010), Portland, OR, USA, September 21–24, pp. 3107–3114. [Google Scholar]
Cite this article as: Vilà-Valls J, Closas P, Curran JT. 2017. Multi-frequency GNSS robust carrier tracking for ionospheric scintillation mitigation. J. Space Weather Space Clim. 7: A26
All Tables
Root mean square phase tracking error considering real scintillation data at different GPS frequency bands for the low scintillation events #3 (t = 200–700s) and #2 (t = 200–700s).
Root mean square phase tracking error considering real scintillation data at different GPS frequency bands for the moderate scintillation events #1 (t = 500–1000s) and #4 (t = 1300–1800s)
Root mean square phase tracking error considering real scintillation data at different GPS frequency bands for the strong scintillation events #3 (t = 2000–2500s), #4 (t = 2000–2500s) and #6 (t = 1700–2200s).
Root mean square phase tracking error considering real scintillation data under modeling mismatch for the severe scintillation event #6 (t = 1700–2200s) and the moderate scintillation event #6 (t = 1300–1700s).
Root mean square scintillation components trackingerror considering real scintillation data for the moderate scintillation event #1 (t = 500–1000s) and the severe scintillation event #3 (t = 2000–2500s).
All Figures
 |
Fig. 1 An example of 100 s of real equatorial scintillation amplitude data for a severe scintillation event at three different GPS frequency bands. |
| In the text | |
 |
Fig. 2 C∕N0 and S4 scintillation index estimation at three GPS frequency bands for two ionospheric scintillation events recorded over Hanoi in March and April 2015. |
| In the text | |
 |
Fig. 3 Empirical model order probability density functions obtained from real multi-frequency ionospheric scintillation data. |
| In the text | |
 |
Fig. 4 Block diagram of the new multi-frequency nonlinear EKF-based architecture. |
| In the text | |
 |
Fig. 5 Estimated scintillation index S4 for the 6 sets of real multi-frequency equatorial scintillation data, i.e., #1 (top) to #6 (bottom). |
| In the text | |
 |
Fig. 6 Steady-state instantaneous dynamics phase estimation error for the moderate scintillation event #1 (t = 200–600s) at L5. |
| In the text | |
 |
Fig. 7 Steady-state instantaneous dynamics phase estimationerror for the severe scintillation event #6 (t = 1800–2200s) at L2. |
| In the text | |
 |
Fig. 8 Scintillation amplitude and phase estimation for the severe scintillation event #3 at L5. |
| In the text | |
 |
Fig. 9 Phaseerror for event #6, GPS L2. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.



