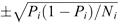| Issue |
J. Space Weather Space Clim.
Volume 8, 2018
Measurement, Specification and Forecasting of the Solar Energetic Particle Environment and GLEs
|
|
|---|---|---|
| Article Number | A37 | |
| Number of page(s) | 14 | |
| DOI | https://doi.org/10.1051/swsc/2018024 | |
| Published online | 24 July 2018 | |
Research Article
Nowcasting of Solar Energetic Particle Events using near real-time Coronal Mass Ejection characteristics in the framework of the FORSPEF tool
1
Institute for Astronomy, Astrophysics, Space Applications and Remote Sensing (IAASARS), National Observatory of Athens, I. Metaxa & Vas. Pavlou St., 15236
Penteli, Greece
2
European Space Research and Technology Centre (ESTEC), Space Environment and Effects Section, Keperlaan 1, 2200AG
Noordwijk, The Netherlands
* Corresponding author: atpapaio@astro.noa.gr
Received:
22
June
2017
Accepted:
11
June
2018
In this work the derived occurrence probability of solar energetic particle (SEP) events (i.e. proton events measured at Earth’s position) and their peak fluxes and total fluences depending on coronal mass ejection (CME) parameters, i.e. linear speed (V) and the angular width (AW) are presented. A new SEP catalogue with associated CME data from 1997 to 2013 is utilized. It is found that the SEP probability strongly depends on the CME speed and the angular width as follows: The highest association (72.70%) is obtained for the full halo CMEs with V ≥ 1500 km s−1 and the lowest association (0.7%) is found for the non halo CMEs with 400 km s−1 ≤ V ≤ 1000 km s−1. The SEP occurrence probabilities are different as much as 26 times according to the CME speed (V), comparing fast versus slow CMEs and 44 times according to the AW, comparing halo to non halo CMEs. Furthermore, linear regressions of the proton peak flux and integral fluence at several integral energy channels (E > 10 MeV, E > 30 MeV, E > 60 MeV, E > 100 MeV) were obtained. Our results, were used to build a module of an operational forecasting tool (i.e. FORecasting Solar Particle Events and Flares – FORSPEF, http://tromos.space.noa.gr/forspef/). This module performs nowcasting (short term forecasting) of SEP events using near real-time CME identifications obtained from CACTus (http://sidc.oma.be/cactus/). The outputs offered by the operational module of the tool to the end user (textural, pictorial, archived data) are presented. Finally, the validation of the system, in terms of archived data is described, in terms of categorical scores (Probability of Detection – POD and a False Alarm Rate – FAR).
Key words: coronal mass ejections / solar energetic particle events / operational system / validation
© A. Papaioannou et al., Published by EDP Sciences 2018
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Solar Energetic Particle (SEP) events are observed as flux increases above a background level, and their energies range from ~10 keV to 10 GeV/nuclei. SEPs consist of electrons, protons, alpha particles and heavier ions up to Fe and their arrival to Earth spans from hours to a few days (Reames, 2015). In the 90’s, the “classical” two-class paradigm that divided SEP events into two categories (impulsive and the gradual) was introduced by Reames (1999). This classification was based on their parent solar events. Impulsive SEP events are considered to be associated to solar flares (SFs), type III radio bursts and have a Fe/O ratio of ≈1; while the gradual ones are considered to be accelerated by coronal mass ejection (CME)-driven shocks, associated with types II and IV radio bursts, and have a ratio of Fe/O ≈ 0.1. In the case of an impulsive SEP event, there are two basic conditions that need to be fulfilled so that an SEP event will be recorded by a detector onboard a spacecraft or ground based. That is that, first of all, particles should get access onto open magnetic field lines and second of all, that the magnetic footpoint of the spacecraft should be well connected to the solar source (e.g. SF), so that flare accelerated particles will be guided along the Interplanetary Magnetic Field (IMF) to the observer (Parker, 1965). In the case of a gradual SEP event, CME-driven shocks are able to inject SEPs over broad angular regions (e.g. Cane et al., 1988; Reames et al., 1996; Rouillard et al., 2012) and the resulting SEP time-profile(s) are organized in terms of the longitude of the observer with respect to the travelling CME-driven shock (Cane & Lario, 2006). Nonetheless, this “two class” picture has proved to be an oversimplification and does not match the diversity and wealth of the observed SEP event properties. Hence, on the one hand, SEP events may incorporate both solar flare-accelerated and CME-accelerated particles, leading to the so-called “hybrid” or “mixed” SEP events (Cliver, 1996), presenting a continuum of event properties (Cane et al., 2010; Papaioannou et al., 2016). On the other hand, a combination of the geometry of the CME-driven shock (quasi-perpendicular or quasi-parallel) and the seed population (i.e. flare suprathermals or ambient solar wind) can explain this large diversity of the event properties recorded onboard spacecraft (Tylka et al., 2005; Tylka & Lee, 2006). At the same time, processes of cross-field diffusion, leading to an effective propagation of particles perpendicular to the average direction of the IMF, may also have an important contribution to the spread of energetic particles in the heliosphere (Zhang et al., 2009; Strauss & Fichtner, 2015). Additionally, transport conditions of SEP events in interplanetary space have an important influence on the recorded time profiles observed at 1 AU (Cohen et al., 2005; Mason et al., 2006; Lario et al., 2016).
The solar origin and the acceleration mechanisms leading to SEP events is still under debate. However, there seems to be a general consensus that the occurrence (or not) of a CME controls the derived probability of the SEP occurrence (Dierckxsens et al., 2015; Kontogiannis et al., 2016). Regular CME monitoring by the Large Angle and Spectrometric Coronograph (LASCO; Brueckner et al., 1995) onboard the Solar and Heliospheric Observatory (SoHO) since 1996 has shown that almost all recorded SEP events during the SoHO era are associated with both CMEs and SFs with only a few events lacking the presence of one or the other (Kurt et al., 2004; Cane et al., 2010; Dierckxsens et al., 2015). Additionally, fast (≥1000 km s−1) and halo CMEs are more likely associated to SEP events, compared to slower and narrower CMEs (Papaioannou et al., 2016; Paassilta et al., 2017). This observational evidence is usually interpreted on the basis of the necessary condition for a shock to be created, i.e. a significant CME velocity. In turn, this CME-driven shock accelerates particles that are consequently driven by the IMF and are routed to a detection system (i.e. the observer) (Kahler & Reames, 2003). At the same a time, it has been reported that halo CMEs, are very energetic and on average faster and wider than all other CMEs; occupy a large volume of the corona; in most cases drive a shock and can be directed either towards or away from the Earth (Gopalswamy et al., 2010). Therefore, it has been suggested that halo CMEs constitute a special class of fast and wide CMEs that differ from the general population of CMEs (Michalek et al., 2003; Lara et al., 2006; Wang et al., 2011). This has been, in principle, verified by studies that employ identifications of CMEs from vantage points within the heliosphere (Nicewicz & Michalek, 2014) e.g. using the coronagraphs onboard the Solar Terrestrial Relations Observatory (STEREO; Kaiser et al., 2008). It is important to note that halo CMEs suffer from strong projection effects, which add to the uncertainty of the identification of halo CME and their corresponding characteristics (Howard et al., 2008).
Kahler (2001) pointed out that the speed of the CME is associated with the intensity of SEP events. Nonetheless, it has been shown that a CME with given characteristics (velocity, width) may as well result in large differences, in the recorded intensity of the SEP events, that extend up to three orders of magnitude (Kahler, 2001; Reames, 2015). Furthermore, the energy of the SEP event under investigation seems to play a significant role in such a correlation with the lower energy particles (E > 10 MeV) presenting a much higher correlation to the CME speed, compared to the higher energy particles (E > 100 MeV) (Dierckxsens et al., 2015). This seems to be the case, also, when investigating the correlation to the fluence of the SEP event (Papaioannou et al., 2016).
Due to the sporadic nature of the SEP events and the far from complete understanding of the mechanisms involved in their generation and the lack of detailed, spatially distributed in-situ observations, their forecasting is not a trivial task. Most of the short-term forecasting systems today rely on soft X-ray (SXR) measurements, which are used for the identification of SFs (Smart & Shea, 1989; Belov et al., 2005; Balch, 2008), on SXR and radio fluence data (Laurenza et al., 2009; Alberti et al., 2017), on in-situ particle measurements of energetic electrons (Posner, 2007) or relativistic protons (Souvatzoglou et al., 2014) and in the combination of both SXR and in-situ proton identification (Nunez, 2011, 2015). However, the usage of CME inputs (velocity and width) as input parameters in an operational SEP forecasting system has not been widely used (Dierckxsens et al., 2015). In particular, the COMESEP SEPForecast Tool (http://comesep.aeronomy.be/alert/) incorporates the outputs of a detailed statistical analysis (Dierckxsens et al., 2015), and makes use of near real-time CME identifications from the “Computer Aided CME Tracking” (CACTus) tool.1 As noted by Dierckxsens et al. (2015), all CMEs of their studied sample were associated with flares, therefore the SEP occurrence probabilities were derived taking into account both flare and CME characteristics (e.g. as a function of longitude and magnitude of the flare for halo CMEs or as a function of longitude, magnitude of the flare and CME velocity for non halo CMEs). As a complementary study to the aforementioned combinations of flare and CME characteristics, these authors, also studied probabilities of SEP occurrence with respect to CME characteristics, alone.
Recently, it has been shown that it is possible to make use of the available near-real time measurements from coronographs to provide warnings of the occurrence of an SEP event (St Cyr et al., 2017). In addition, over the last years, several tools that provide automated identifications of solar eruptions and consequently information on the CME occurrence, and on their expected characteristics, have been developed by the scientific community. Such solutions include: CACTus (Robbrecht & Berghmans, 2004), the solar eruptive event detection system (SEEDS; Olmedo et al., 2008) and the automated CORIMP catalogue (Byrne, 2015). Hence, it is in principle possible to utilize each (or to select one) of these aforementioned tools to serve as an input for the short-term forecasting of SEP events, based on CME identifications. Each tool has advantages and disadvantages. For example, as concerns data availability, both CACTus and SEEDS operate in near-real time and detections of CMEs can be found online on a daily basis, while CORIMP has a delay of ≈2–3 days. CACTus and SEEDS provide identification for the same CME event with minor differences with respect to the derived CME characteristics (e.g. angular width, speed). However, CACTus seems to identify more CME events than SEEDS and for this reason is used in this work.
In this work, we introduce a concept that utilizes near-real time identification of CME characteristics from CACTus and provides short-term forecasting of the occurrence of an SEP event, as well as, estimations of its corresponding characteristics (peak proton flux and total fluence). This concept has been incorporated in and operates under the FORSPEF tool (Papaioannou et al., 2015; Anastasiadis et al., 2017). The paper is structured as follows: Section 2 discusses the data that were used as the basis for putting the concept in context, Section 3 provides a detailed description of the methodology and its corresponding implementation, Section 4, gives an overview of the operational tool and the capabilities offered to the end user. Section 5 presents the validation through the construction of the corresponding categorical scores and Section 6 discusses the obtained results, as well as, the strengths and weaknesses of the proposed approach.
2 Data and analysis
To develop the CME-forecasting tool, we utilize the CME identifications made by LASCO (Brueckner et al., 1995) onboard SoHO in the period 1997–2013. These identifications are included in the Coordinated Data Analysis Web (CDAW) online CME Catalog2 at http://cdaw.gsfc.nasa.gov/CME_list/ (Gopalswamy et al., 2009). In particular, we make use of the plane-of-sky speeds and the angular widths of the CMEs as those are reported in the CDAW CME Catalog.
Moreover, we utilize a part of a new catalogue of SEP events that initially included 314 SEP events from 1984–2013, that was recently developed by our group (Papaioannou et al., 2016). The sample that we are using covers the time span for which CME data were available (i.e. 1997–2013). This SEP event catalogue is based on Geostationary Operational Enviromental Satellite (GOES)/Energetic Particle Sensor (EPS) data (Rodriguez et al., 2014) and it includes key information on the proton peak flux and the total fluence of the identified SEP events in four integral energy channels (E > 10; >30; >60; >100 MeV). It further includes the associated solar sources of the SEP events in terms of solar flares and CME characteristics. In order to estimate the probability of SEP occurrence, we utilize both datasets (i.e. catalogues) and we make use of 1905 CMEs and 158 SEP events (E > 10 MeV) in the analysis.
3 Results
3.1 Solar energetic particle event occurrence probability
We consider two-dimensional SEP occurrence probabilities depending on CME speed and angular width (Park et al., 2012). In order to do so we divided the CMEs into nine (9) subgroups according to their characteristics. There are three CME speed ranges: slow (400 km s−1 ≤ V < 1000 km s−1), moderate (1000 km s−1 ≤ V < 1500 km s−1), and fast (V ≥ 1500 km s−1) and three angular width ranges: full halo (AW = 360°), partial halo (120° ≤ AW ≤ 359°) and non halo (AW < 120°). Table 1 represents the derived SEP probabilities, defined as: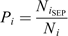 (1)where N
i
is the total number of CMEs in the subset i and
(1)where N
i
is the total number of CMEs in the subset i and 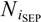 is the number of those events that resulted in an observed SEP event, for the nine (9) subgroups depending on the CME speed and the angular width range.
is the number of those events that resulted in an observed SEP event, for the nine (9) subgroups depending on the CME speed and the angular width range.
Solar energetic particle events occurrence probability depending on three CME speed ranges and three angular width ranges of CMEs, as obtained by Equation (1). The values within the brackets denote the error calculated from Equation (2). The values within the parenthesis correspond to 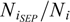 per i bin.
per i bin.
The respective error is: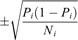 (2)corresponding to a 68% confidence level when the sample is described by a normal distribution (Dierckxsens et al., 2015).
(2)corresponding to a 68% confidence level when the sample is described by a normal distribution (Dierckxsens et al., 2015).
Our results show that the probabilities increase with CME speed (V) and AW. The probability of SEP occurrence for all nine subgroups is 8.08% (154/1905) (see Table 1). The highest probability is 72.7% for the subgroup with fast and full halo CMEs. The lowest one is 0.7% for the subgroup of CMEs with slow and non halo CMEs. A comparison of the obtained probabilities for these two groups (i.e. fast and halo vs. slow and non halo) shows a difference of 103 times, which, in turn, quantifies the divergence between the high and the low ends of the obtained probabilities. In the case of CME speed ranges, the total probabilities are ordered as: 2.64%, 26.56%, and 67.4% from the slow CME group to the fast CME group, respectively. The probability of the fast CME group is ≈26 times larger than that of the slow CME group. In the case of the CME AW, the total probabilities are 0.9% in the non halo CME subgroup, 11.4% in the partial halo CME subgroup and 39.4% in the full halo CME subgroup. The probability of the full halo CME group is ≈3.5 times larger than that of the partial halo CME group and ≈44 times larger compared to the non halo CME group.
As a next step, for the obtained probabilities of Table 1, we applied several functions in order to derive an optimal fit to the data. Table 2 gives these corresponding fits. Column 1 refers to the CME type (Halo, Partial Halo and Non Halo CMEs). Column 2 indicates the fitted curve per CME type. Column 3 presents the actual function and column 4 indicates the coefficient of determination (R 2). One should note that the obtained fits include a level of uncertainty, due to the small number of bins with respect to the CME velocity. At the same time, the number of CMEs (and CMEs associated to SEP events) is rather small to allow for a finer binning. Nonetheless, as a cross-validate measure, we have applied the CME binning proposed by Evans et al. (2013) and the obtained results preserved the trends of the fits within less than 10% (not shown).
Probability of SEP Occurrence Functions per CME type.
The derived SEP occurrence probabilities per CME angular width group from Table 1 are illustrated in Figure 1 (halo CME: blue, partial halo: red, non halo: green) as a function of CME speed, and includes the optimal derived fits listed in Table 2.
 |
Fig. 1. The derived SEP occurrence probabilities for all nine subgroups and the obtained fits per angular width of the CME. The blue line corresponds to Halo CMEs (AW = 360°), the red line to Partial Halo CMEs (120° ≤ AW ≤ 359°) and the green line corresponds to non halo CMEs (AW < 120°). The best fits are presented in Table 2. The error bars are calculated as: |
3.2 Relationship between the CME speed and the proton peak flux
The relationship between the speed of the CME (V), the logarithm of the proton peak flux of the SEP events and its dependence on the AW of the CME is studied in this section.
In particular, linear regressions, per integral energy and CME width type are identified. In practice, the AW of the CME identifies the appropriate fit (Table 3) and the speed of the CME returns the expected value of the logarithm of the proton peak flux for the forthcoming SEP event. Column 1 of Table 3 presents the width type of the CME (Halo, Partial Halo, Non Halo), column 2 refers to the integral proton energy channel (E > 10 MeV, E > 30 MeV, E > 60 MeV, E > 100 MeV) per CME type, column 3 provides the linear regression in each case, column 4 displays the relevant Pearson’s correlation coefficient cc and the respective standard error SE
cc
, which is calculated as: 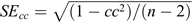 with n being the number of pairs used for the calculation of cc. This number (n) is included in Table 3 for every case.
with n being the number of pairs used for the calculation of cc. This number (n) is included in Table 3 for every case.
Linear regressions for the logarithm of the SEP Proton Peak Flux per CME width type and integral energy channel. Pearson’s correlation coefficients (cc), as well as their standard error SE cc are also presented, where n is the number of pairs used for the calculation of cc.
The relation of the CME speed to the logarithm of the SEP proton peak flux at several integral energy channels (E > 10 MeV, E > 30 MeV, E > 60 MeV, E > 100 MeV) and its dependence on the angular width type of the CME, per integral energy channel from Table 3 is illustrated in Figure 2. Halo CMEs (left hand side column, blue color), partial halo CMEs (middle column, red color) and non halo CMEs (right hand side column, green color). Each panel of Figure 2 provides the calculated Pearson’s correlation coefficient (cc) and the standard error (SEcc).
 |
Fig. 2. Linear regressions between the CME speed and the logarithm of the SEP proton peak flux at several integral energy channels. The first column (stack of four plots) provides the regressions for the Halo CMEs (blue color). The second column shows the regressions for the Partial halo CMEs (red color) and the third column includes the regressions for the non halo CMEs (green color). For each column, from top to bottom the corresponding integral energy channels are E > 10 MeV, E > 30 MeV, E > 60 MeV and E > 100 MeV |
 |
Fig. 3. Linear regressions between the CME speed and the logarithm of the SEP fluence at several integral energy channels. Similar to Figure 2. |
3.3 Relationship between the CME speed and the integral fluence of the SEP event
Similar to Section 3.2, the relationship between the speed of the CME (V), the logarithm of the fluence of the SEP events and its dependence on the angular width group of the CME is studied in this section. Again, we make use of linear regressions, per integral energy and CME type. Column 1 of Table 4 presents the width type of the CME (halo, partial halo, non halo), column 2 refers to the integral proton energy channel (E > 10 MeV, E > 30 MeV, E > 60 MeV, E > 100 MeV) per CME type, column 3 provides the linear regression at each case, column 4 displays the relevant Pearson’s correlation coefficient cc and the respective standard error SEcc .
The relation of the CME speed and the logarithm of the SEP fluence at several integral energy channels (E > 10 MeV, E > 30 MeV, E > 60 MeV, E > 100 MeV) and its dependence on the angular width of the CME, per energy channel, from Table 4 is presented in Figure 3, similar to Figure 2. Halo CMEs (left hand side column, blue color), partial halo CMEs (middle column, red color) and non halo CMEs (right hand side column, green color). Furthermore, the calculated Pearson’s correlation coefficient (cc) and the standard error (SE cc ), are presented on each panel of Figure 3.
4 Operational module
The FORSPEF tool is a new integrated solution for the forecasting and/or nowcasting (short term forecasting) of SEP events, targeted to spacecraft and launch operators (Papaioannou et al., 2015; Anastasiadis et al., 2017). It utilizes a set of different modules and provides forecasting of SFs based on magnetograms and a sequential forecasting of the occurrence of the SEP events based on the derived SF probability. Moreover, it incorporates different sub-modules for the short-term forecasting (nowcasting) of SEP events. Each sub-module makes use of a single data set/proxy. Hence, there is a sub-module that makes use of SF data (longitude and magnitude), another sub-module that uses CME identifications (width and velocity) and a final sud-module that takes advantage of the ESPERTA (Empirical model for Solar Proton Event Real Time Alert) model, utilizing the location and the size of SFs together with evidence of particle escape (i.e. type III radio bursts) (Laurenza et al., 2009; Alberti et al., 2017). The FORSPEF system has been online since April 2015 at http://tromos.space.noa.gr/forspef/ and provides continuous forecasts and nowcasts of SFs and SEP events. Registration for notifications is free charge and can be done via the website.
As already been pointed out, here above, currently there are several automated solutions that provide near real-time identifications of CMEs. For a brief comparison between CACTus, SEEDS and CORIMP one may notice that: (i) CACTus (http://sidc.oma.be/cactus/) makes use of both C2 and C3 LASCO detectors and is robust in reproducing detections of CMEs identified manually, as becomes evident when comparing its outputs to those of the CDAW CME catalog; (ii) SEEDS (http://spaceweather.gmu.edu/seeds/) uses only C2 identifications and thus presents some overestimations of the CME angular width due to streamer deflections; (iii) CORIMP (http://alshamess.ifa.hawaii.edu/CORIMP/) provides very sophisticated and detailed outputs. However, it is not a near-real-time tool and the data (outputs) availability has a time lag of several days. To this end, we have chosen to make use of the CACTus online solution. The package is extensively described in Robbrecht & Berghmans (2004) and its output is available online at http://sidc.oma.be/cactus/. It is designed to detect CMEs in coronagraph images, thus the input to the CACTus software is a time sequence of observational data obtained from both the LASCO C2 and C3 coronagraphs. A typical output of CACTus shows the detected events in a synoptic diagram, including the characteristics per event like the onset time, the principle angle (the projection of the principle direction of an event on the field-of-view), the angular width, and the velocity estimation (Bonte et al., 2011).
The sequence of the operational set up of the FORSPEF’s sub-module that makes use of the near-real time CME identifications from CACTus is illustrated in Figure 4. The steps followed by the software are the following. First we read in the CACTus output (width and velocity) provided online at: http://www.sidc.oma.be/cactus/out/cmecat.txt, for each identified CME. Then, based on the angular width the software selects the appropriate fit (see Fig. 1) and given the speed of the CME the probability of SEP occurrence is identified. To calculate the expected SEP characteristics (proton peak flux – Table 3 and total fluence – Table 4) for a given CME at a set of integral energy channels (E > 10; >30; >60 and >100 MeV) the linear regressions defined by the AW of the CME are used. All of these outputs are presented through the web interface of the FORSPEF tool in near real-time at http://tromos.space.noa.gr/forspef/. Furthermore, the outputs (nowcasts) are stored in a local database and the users of the FORSPEF tool may have unrestricted access via the “Archive” option (http://tromos.space.noa.gr/forspef/archive/), while a near-real time notification tool (http://tromos.space.noa.gr/forspef/notifications/) informs registered users when an SEP event is expected to take place.
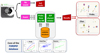 |
Fig. 4. A block diagram of the operational set up of FORSPEF’s sub-module based on CACTus near real-time CME identifications. |
5 Validation
5.1 Probability of detection
In order to validate the proposed methodology it is possible to construct categorical scores (Balch, 2008). In particular, we employ the probability of detection (POD), the false alarm rate (FAR), the Heidke Skill Score (HSS) and the Percent Correct (PC) quality measures, all of which, are functions of a probability threshold (pt). The mapping of the probabilistic short-term forecasts into categorical measures requires the implementation of a contingency table which includes five values:
-
A: the number of Hits, which correspond to the number of SEP events that were forecasted to occur and actually took place.
-
B: the number of false positives, which correspond to the number of SEP events that were forecasted to occur but no actual event took place.
-
C: the number of Missed events, which correspond to the number of SEP events that were not forecasted to occur but an event actually took place.
-
D: the number of true negatives, which correspond to the number of SEP events that were not forecasted to occur and no actual event took place.
-
N: the total number of forecasts, i.e. N = A + B + C + D.
Based on these four values, the categorical measures are defined as follows:
-
POD = A/(A + C)
-
FAR = B/(A + B)
-
PC = (A + D)/N
-
HSS = 2(AD − BC)/[(A + C)(C + D) + (A + B)(B + D)]
Aiming at evaluating the efficiency of the CME nowcasting model and to construct the categorical measures, we have chosen to scan proton data at an integral energy channel of E > 10 MeV, as measured by the Space Weather Prediction Center (SWPC) primary GOES satellite and to identify the SEP events that were recorded from 2013 (April) to 2015 (September). The data used in this part of the analysis were retrieved at https://satdat.ngdc.noaa.gov/sem/goes/data/. This is because, we opt for totally independent control and test samples. Since the software was built upon the data made available from 1997 to 2013 (March) (see Sect. 2), our control sample already covered this time span. Hence, the extension to a time period that was not covered by our control sample was mandatory. As a result of the scanning, 43 SEP events were selected (Table 5). Column 1 provides the event number, column 2 the date of the CME that was associated to the SEP event, column 3 the time of identification of the CME at its first appearance within the C2 FOV, column 4 shows the AW of the CME in degrees, column 5 gives the plane-of-sky velocity of the CME in km s−1, column 6 provides the obtained probability of SEP occurrence per CME based on the fits of Figure 1, column 7 identifies the events as a Hit or a Miss based on a probabilistic threshold of pt = 0.30 and column 8 is similar to column 7 but for a probabilistic threshold of pt = 0.25. This latter value corresponds to the probabilistic level that was identified applying a different approach for the validation of the model; in particular, the FORSPEF’s nowcasting module based on CME data, was validated using ten (10) different randomly picked control and test samples spanning from 1997 to 2013 (Anastasiadis et al., 2017). As a result, the mean POD – out of the 10 different pairs of samples – was 70% and the mean FAR was 41%.
SEP CME list (04.2013–09.2015).
5.1.1 Categorical scores I
The derived categorical scores for E > 10 MeV are presented in Figure 5. An examination of the plot shows that for low levels of probabilistic thresholds (<0.20) both POD (red curve) and FAR (blue curve) are very high (≈90%) and both decrease when pt increases (Fig. 5). We also see that the optimal skill score (using HSS) is achieved at the range of probabilities (pt) from 20 to ≈50%. This result is consistent with our previous results (Anastasiadis et al., 2017). HSS is maximized at a pt value equal to 0.30. At this point, the corresponding POD is 65% while FAR is 58%. This underlines the fact that even at the point of optimal skill the number of false alarms and missed events is still significant and there is clearly room for improvement. In particular out of the 43 SEP events identified in this work (see Table 5) the module is in place to identify 28/43 events while it misses 15/43 events at a threshold of pt = 0.30 (see column 7 of Table 5). If we utilize the threshold from Anastasiadis et al. (2017), pt = 0.25, the module identifies 31/43 SEP events and misses 12/43 (see column 8 of Table 5). At the same time the number of false positives is significant, being 39 in the first case (pt = 0.30) and 43 in the second case (pt = 0.25).
 |
Fig. 5. Categorical performance statistics for the FORSPEF CME module as a function of probability thresholds for E > 10 MeV covering 2013–2015. |
Table 6, summarizes the POD and FAR for higher energies (i.e. E > 30, E > 100 MeV), per probability threshold (pt). It provides the constructed contingency tables per energy and pt and furthermore it presents the achieved POD and FAR.
Summary of the categorical scores (POD, FAR) for higher energies, per pt. A corresponds to Hits, B to false positives, C to misses and D to true negatives.
5.1.2 Categorical scores II
As a next step, we updated our database of solar flares and CMEs, applying the methodology detailed in Papaioannou et al. (2016) and thus extended our sample until the end of 2015. Our goal was to utilize the whole time span from the beginning of Solar Cycle 23, i.e. 1997 until 2015, similar to Anastasiadis et al. (2017). We identified 12936 solar flares, 3944 different CMEs, 201 SEP events within this time span. Out of these, we randomly selected ≈85% of the solar flares (i.e. 10,536 solar flares), as the control sample, and the rest (15%) were treated as the test sample, with the selection of the test and control samples being completely random. This procedure was repeated ten times, and ten different completely independent control and test samples were obtained. For all paired samples (control and test) we applied categorical quality measures for POD, FAR, HSS, and PC.
An indicative example of the derived categorical scores is presented in the left hand side panel of Figure 6, whereas, the right hand side panel of Figure 6, depicts the obtained POD and FAR per number of trial. The mean POD – out of the 10 different pairs of samples – is 70% and the mean FAR was 44%, which is consistent with the results presented in Anastasiadis et al. (2017).
 |
Fig. 6. An indicative example of the categorical performance statistics for the CME module as a function of probability thresholds (panel on the left) and the obtained POD and FAR for all 10 different trials, depicted as circles (panel on the right). The obtained POD and FAR from the initial sample (see Sect. 5.1.1 and Figure 5) are also marked in this latter panel as triangles, for comparison. |
5.2 SEP characteristics
The predicted peak proton flux at E > 10; E > 30 and E > 100 MeV for all SEP events of Table 5 was then calculated. The predicted peak flux versus the observed peak flux per energy is presented in Figure 7. In order to perform this validation step, we have used the GOES data, available at: https://satdat.ngdc.noaa.gov/sem/goes/data/new_avg/. We have consequently scanned the data for the integral energy channels of E > 10; >30 and >100 MeV and identified the peak proton flux for each event at these respective energies. As a second step, aiming at validating our obtained results for the peak proton fluxes from the aforementioned scanning, we performed a cross-check of our identifications for the peak proton flux at E > 10 MeV with the values presented in the standard NOAA SEP list, available at ftp://ftp.swpc.noaa.gov/pub/indices/SPE.txt. At this point, one should note that out of the 43 SEP events listed in Table 5, there were 42 for which a peak proton flux value was identified at E > 10 MeV. This is because there were data gaps for one event (Event on 13.12.2014, No. 33 in Table 5) that made such an identification ambiguous and therefore was not included in this part of the validation. Furthermore, we could identify 33 and 15 SEP events that had a pronounced peak in E > 30 MeV and E > 100 MeV, respectively. Therefore, each panel of Figure 7 corresponds to a different integral energy (i.e. the left hand panel corresponds to E > 10 MeV and includes a total of n = 42 events; the middle panel corresponds to E > 30 MeV and refers to n = 33 events and the right hand panel corresponds to E > 100 MeV and includes n = 15 events). The corresponding correlation coefficients (cc) per energy are: E > 10 MeV: 0.198 (n = 42); E > 30 MeV: 0.235 (n = 33) and E > 100 MeV: 0.173 (n = 15). Although there is significant scatter from the perfect dichotomous prediction line at each energy, in most cases (≈74%) the predictions are within one order of magnitude of the observations, but not always. These results, underline the inherent difficulty for the SEP characteristics prognosis (Balch, 2008; Anastasiadis et al., 2017).
 |
Fig. 7. Comparison of the observed with the predicted peak proton flux for the SEP events listed in Table 5. Each plot corresponds to a specific provided energy and includes the number of SEP events that reach this energy; see text for details. |
6 Discussion and conclusions
In this work, we have reported on a new, operational module for the short-term forecasting (nowcasting) of SEP events (probability of occurrence and their corresponding characteristics) using near-real time CME identifications. The module has been developed within the FORSPEF tool and is in continuous operation (http://tromos.space.noa.gr/forspef/) and builds on three main analyses that were presented in this paper.
-
Two dimensional (2D) SEP occurrence probability dependence on CME parameters
Empirical relations were introduced for the short-term forecasting of SEP events using CME identifications based on a statistical data driven approach. The probability of SEP occurrence is given as a function of two CME parameters (velocity (slow, moderate, and fast) and angular width group (non halo, partial halo and full halo), see Table 1). Outputs as concerns the observed trends in the results are found to be comparable with results obtained by Park et al. (2012). Several limitations are imposed by the actual data used in the analysis. For instance we employ the plane-of-sky speed and the width of the CME, both of which are identified through projections and can only be considered as an indicator of the CME activity that often includes under or over estimations.
-
Fits to the 2D probabilities
These fits provide the expected probability of SEP occurrence for a CME with a given width and speed. Moreover, the derivation of the 2D probabilities (Fig. 1) shows that in the case of non halo and especially in the third bin (fast CMEs) the error is quite significant. This is because of the very small number of CMEs included in this bin, which dramatically increases the uncertainty. At the same time, the fits incorporate a level of inherent uncertainty based on the applied binning.
-
Scatter plots of observed versus predicted SEP peak proton fluxes at different energies to quantify the capabilities of the proposed context.
6.1 Validation of SEP forecasting
Using categorical quality measures, the performance of the FORSPEF CME module was validated and results were interpreted. The results presented in this work are reasonably typical for SEP forecasting methods (see Table 1 in Anastasiadis et al., 2017), which range around a POD of 60% and a FAR of 40% (Balch, 2008; Laurenza et al., 2009; Alberti et al., 2017; Anastasiadis et al., 2017). In particular, for an independent test sample spanning from 2013 to 2015 (see Table 5) and for an optimal probability threshold (pt = 0.30) POD is 65% and FAR is 58% (see Sect. 5.1.1). Additionally, the mean POD is 70% and the mean FAR is 44% for 10 independent randomized control and test samples spanning from 1997 to 2015 (see Sect. 5.1.2).
Investigating further the obtained FAR of 58% (see Sect. 5.1.1), it was found that the number of false positives (B) is mainly populated by fast (V > 850 km s−1) and halo CMEs (34/39 and 39/43 respectively for each threshold). As it is known, solar cycle (SC) 24 (which is represented in our test sample, spanning from 2013 to 2015) has proven to be an irregular SC with the rate of CMEs being higher and their width being larger compared to the CMEs of SC23. Additionally, a larger fraction of halo CMEs is spotted among the CMEs of SC24 (Gopalswamy et al., 2014). At the same time, although CMEs are found to drive shocks, and that the number of SEP events with E > 10 and E > 100 MeV in SC 24 is comparable to the relevant number of previous cycles (Bazilevskaya et al., 2015; Richardson et al., 2016), those CMEs are not efficient in accelerating particles to higher energies (Paassilta et al., 2017). However, recently, Alberti et al. (2017), showed that there is an observed 40% reduction in SEP activity between two selected intervals in SC23 (15.09.1996–15.09.2002) and SC24 (15.12.2008–15.12.2014). This reduction was not attributed to a lack of halo CMEs in SC24, but could probably be explained by lower large-scale magnetic activity (i.e., active regions and sunspot areas), or the presence of CMEs producing seed particles – as noted by the authors of this paper. In addition, Vainio et al. (2017) discussed this lack of high-energy SEP events from the point of view of shock acceleration in self-generated waves, and showed that it could be explained as being due to decreased fluxes of suprathermal seed particles rather than the decreased magnetic field. In agreement with Alberti et al. (2017), not every halo CME of SC24 in our sample was associated to an SEP event. Whatever the case may be, as concerns the presence of halo CMEs in SC24 it shows that the irregularity of this cycle affects the performance of the software presented in this work and significantly elevates the number of false positives. At the same time, when applying a random separation of control and trial samples, the differences in the properties of the solar cycles (e.g. SC23 and 24) seem not to affect the performance of the tool since we obtained categorical scores similar to Anastasiadis et al. (2017).
6.2 Conclusions and perspectives
The basic findings presented in this study are summarized as follows:
-
The probabilities of SEP occurrence increases with respect to the velocity of the CME. In particular, the probabilities for fast CMEs (67.4%) are much larger than those with moderate CMEs (26.56%) and slow CMEs (2.64%). Moreover, the probabilities are 12.4% for the partial halo CME group and 39.40% for the full halo CME group, i.e. the presence or not of a halo CME triples approximately the probability for SEP occurrence.
-
The probability results are also considered in the context of categorical forecast performance measures. The optimal HSS is achieved using a probability threshold in the range 20–30% range. We showed that at this optimal probability threshold (pt = 0.30) FAR is 58% and POD is 65%, for the test sample presented in Section 5. At the same time, when applying the procedure detailed in Anastasiadis et al. (2017), we obtained a mean POD of 70% and a mean FAR of 44%, with the analysis performed on randomly selected control and trial samples.
To our knowledge, the usage of CME identifications (e.g. angular width and speed) for the derivation of the SEP occurrence probabilities have been explored by few operational systems, one being the COMESEP SEPForecasting tool. However, this tool predicts the probability and level for a radiation storm with proton energies >10 MeV and >60 MeV resulting from a flare (>M class), incorporating – if available – information like the location of the flare (longitude), CME speed and width (the latter when AW > 150°) and when a significant SEP event (E > 433 MeV) (i.e. Ground Level Enhancement – GLE) occurs. Hence, the characteristics of the CME are utilized once an >M-class flare has already occurred. In contrast, the module that is presented in this work utilizes: (i) solely CME identifications – not considering related flare characteristics and (ii) CMEs of any width (i.e. 0–360°) (iii) provides identifications for four energy ranges, i.e. >10, >30, >60 and >100 MeV. As it was shown in this work, the identification of SFs is not a necessary condition when deriving SEP occurrence probabilities. This is in line with the study of Dierckxsens et al. (2015; their Fig. 12). However, it should be noted that the SEP occurrence probability as a function of SF magnitude, SF longitude and CME velocity seem to increase when utilizing SF-CME couples situated on the west part of the visible solar disk (Dierckxsens et al., 2015), which – in turn – points to the prominent role of the magnetic connection.
We believe that this is a first step towards a more sophisticated forecasting tool that should be further combined with other proxies and data leading to an integrated solution. In general, the significant high FAR value suggests that many more parameters that need to be taken into account, in order to build a reliable and more accurate SEP forecasting system. For example, an attempt to further exploit the possible direction of a CME could be examined. For example, the B eff metric3 has been associated to the maximum velocity of CMEs (Georgoulis, 2008) and has been utilized for the identification of the CME likelihood (Papaioannou et al., 2015; Anastasiadis et al., 2017). Therefore, it is not un-probable to connect the dots and from the calculated B eff of an active region to be led to the expected probability of SEP occurrence.
Acknowledgments
This work was supported through the ESA Contract No. 4000109641/13/NL/AK “Improvement of Solar Particle Events and Flare Prediction”. AP would like to acknowledge support from a post-doctoral IKY scholarship funded by the action “Supporting post-doctoral researchers” from the resources of the b.p. “Human Resources Development Education and Lifelong Learning” with Priority Axes 6,8,9 and co-funded by the European Social Fund and the Greek government. AA acknowledges the support through “SPECS: Solar Particle Events and foreCasting Studies” Research grant of the National Observatory of Athens. The CME Catalog used in this work is generated and maintained at the CDAW Data Center by NASA and The Catholic University of America in cooperation with the Naval Research Laboratory. Funding for the early phase of the catalog was provided by AFOSR and NSF. Currently, the catalog resides at the CDAW Data Center at Goddard Space Flight Center and is supported by NASA’s Living with a Star program and the SOHO project. SOHO is a project of international cooperation between ESA and NASA. The module presented in this work uses data from the CACTus CME catalog, generated and maintained by the SIDC at the Royal Observatory of Belgium. The authors would like to thank Rami Vainio, Norma Crosby and another anonymous referee for their constructive comments and assistance that helped improve the initial manuscript. The editor thanks Norma Crosby and an anonymous referee for their assistance in evaluating this paper.
B eff is the effective connected magnetic field strength -- for details see Anastasiadis et al (2017).
References
- Alberti T, Laurenza M, Cliver E, Storini M, Consolini G, Lepreti F. 2017. Solar activity from 2006 to 2014 and short-term forecasts of solar proton events using the ESPERTA model. ApJ 838 (1): 59. [Google Scholar]
- Anastasiadis A, Papaioannou A, Sandberg I, Georgoulis M, Tziotziou K, Kouloumvakos A, Jiggens P. 2017. Predicting flares and solar energetic particle events: The FORSPEF tool. Sol Phys 292 (9): 134. [Google Scholar]
- Balch CC. 2008. Updated verification of the Space Weather Prediction Center’s solar energetic particle prediction model. Space Weather 6 (1): 1–13. [Google Scholar]
- Bazilevskaya G, Logachev YI, Vashenyuk E, Daibog E, Ishkov V, et al. 2015. Solar proton events in solar activity cycles 21–24. Bull Russ Acad Sci Phys 79 (5): 573–576. [CrossRef] [Google Scholar]
- Belov A, Garcia H, Kurt V, Mavromichalaki H, and Gerontidou M. 2005. Proton enhancements and their relation to the X-ray flares during the three last solar cycles. Sol Phys 229 (1): 135–159, [CrossRef] [Google Scholar]
- Bonte K, Jacobs C, Robbrecht E, De Groof A, Berghmans D, Poedts S. 2011. Validation of CME detection software (CACTus) by means of simulated data, and analysis of projection effects on CME velocity measurements. Sol Phys 270 (1): 253–272. [Google Scholar]
- Brueckner G, Howard R, Koomen M, Korendyke C, Michels D, et al. 1995. The large angle spectroscopic coronagraph (LASCO). Sol Phys 162 (1–2): 357–402. [CrossRef] [Google Scholar]
- Byrne JP. 2015. Investigating the kinematics of coronal mass ejections with the automated CORIMP catalog. J. Space Weather Space Clim 5: A19. [Google Scholar]
- Cane H, Lario D. 2006. An introduction to CMEs and energetic particles. Space Sci Rev 123 (1–3): 45–56. [NASA ADS] [CrossRef] [Google Scholar]
- Cane H, Reames D, Rosenvinge T. 1988. The role of interplanetary shocks in the longitude distribution of solar energetic particles. J Geophys Res: Space Phys 93(A9): 9555–9567. [Google Scholar]
- Cane H, Richardson I, Von Rosenvinge T. 2010. A study of solar energetic particle events of 1997–2006: Their composition and associations. J Geophys Res: Space Phys (1978–2012) 115(A8): 1–18. [Google Scholar]
- Cliver E. 1996. Solar flare gamma-ray emission and energetic particles in space. In: High energy solar physics, vol. 374, AIP Publishing, Melville, NY, 45–60. [NASA ADS] [CrossRef] [Google Scholar]
- Cohen C, Stone E, Mewaldt R, Leske R, Cummings A, Mason G, Desai M, von Rosenvinge T, Wiedenbeck M. 2005. Heavy ion abundances and spectra from the large solar energetic particle events of October–November 2003. J Geophys Res: Space Phys 110(A9): 1–15. [CrossRef] [Google Scholar]
- Dierckxsens M, Tziotziou K, Dalla S, Patsou I, Marsh M, Crosby N, Malandraki O, Tsiropoula G. 2015. Relationship between solar energetic particles and properties of flares and CMEs: Statistical analysis of solar cycle 23 events. Sol Phys 290 (3): 841–874. [Google Scholar]
- Evans RM, Pulkkinen AA, Zheng Y, Leila Mays M, Taktakishvili A, Kuznetsova MM, Hesse M. 2013. The SCORE scale: A coronal mass ejection typification system based on speed. Space Weather 11 (6): 333–334. [NASA ADS] [CrossRef] [Google Scholar]
- Georgoulis MK. 2008. Magnetic complexity in eruptive solar active regions and associated eruption parameters. Geophys Res Lett 35 (6): 1–5. [CrossRef] [Google Scholar]
- Gopalswamy N, Akiyama S, Yashiro S, Xie H, Makela P, Michalek G. 2014. Anomalous expansion of coronal mass ejections during solar cycle 24 and its space weather implications. Geophys Res Lett 41 (8): 2673–2680. [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy N, Yashiro S, Michalek G, Stenborg G, Vourlidas A, Freeland S, Howard R. 2009. The SOHO/LASCO CME Catalog. Earth Moon Planets 104: 295–313, DOI: 10.1007/s11038-008-9282-7. [NASA ADS] [CrossRef] [Google Scholar]
- Gopalswamy N, Yashiro S, Michalek G, Xie H, Makela P, Vourlidas A, Howard R. 2010. A catalog of halo coronal mass ejections from SOHO. Sun and Geosphere 5 (1): 7–16. [Google Scholar]
- Howard T, Nandy D, Koepke A. 2008. Kinematic properties of solar coronal mass ejections: Correction for projection effects in spacecraft coronagraph measurements. J Geophys Res: Space Phys 113(A1): 1–12. [Google Scholar]
- Kahler S. 2001. J Geophys Res: Space Phys 106(A10): 20947–20955. [Google Scholar]
- Kahler S, Reames D. 2003. Solar energetic particle production by coronal mass ejection-driven shocks in solar fast-wind regions. ApJ 584(2), 1063. [NASA ADS] [CrossRef] [Google Scholar]
- Kaiser ML, Kucera T, Davila J, Cyr OS, Guhathakurta M, Christian E. 2008. The STEREO mission: An introduction. Space Sci Rev 136 (1–4), 5–16. [CrossRef] [Google Scholar]
- Kontogiannis I, Belehaki A, Tsiropoula G, Tsagouri I, Anastasiadis A, Papaioannou A. 2016. Building a new space weather facility at the National Observatory of Athens. Adv Space Res 57 (1): 418–430. [CrossRef] [Google Scholar]
- Kurt V, Belov A, Mavromichalaki H, Gerontidou M. 2004. Statistical analysis of solar proton events. Ann Geophys 22(6), 2255–2271. [NASA ADS] [CrossRef] [Google Scholar]
- Lara A, Gopalswamy N, Xie H, Mendoza-Torres E, Perez-Eriquez R, Michalek G. 2006. Are halo coronal mass ejections special events? J Geophys Res Space Phys 111(A6): 1–12. [Google Scholar]
- Lario D, Kwon R-Y, Vourlidas A, Raouafi N, Haggerty D, et al. 2016. Longitudinal properties of a widespread solar energetic particle event on 2014 February 25: evolution of the associated CME shock. ApJ 819 (1): 72. [NASA ADS] [CrossRef] [Google Scholar]
- Laurenza M, Cliver E, Hewitt J, Storini J, Ling A, Balch C, Kaiser M. 2009. A technique for shortterm warning of solar energetic particle events based on flare location, flare size, and evidence of particle escape. Space Weather 7 (4): 1–18. [Google Scholar]
- Mason GM, Desai MI, Cohen C, Mewaldt RA, Stone EC, Dwyer JR. 2006. The role of interplanetary scattering in western hemisphere large solar energetic particle events. Astrophys J Lett 647 (1): L65. [NASA ADS] [CrossRef] [Google Scholar]
- Michalek G, Gopalswamy N, Yashiro S. 2003. A new method for estimating widths, velocities, and source location of halo coronal mass ejections. ApJ 584 (1): 472. [NASA ADS] [CrossRef] [Google Scholar]
- Nicewicz J, Michalek G. 2014. Testing the asymmetric cone model for halo CMEs using STEREO/SECCHI coronagraphic observations. Adv Space Res 54 (4): 780–787. [CrossRef] [Google Scholar]
- Nunez M. 2011. Predicting solar energetic proton events (E > 10 MeV). Space Weather 9 (7): 1–28. [CrossRef] [Google Scholar]
- Nunez M. 2015. Real-time prediction of the occurrence and intensity of the first hours of > 100 MeV solar energetic proton events. Space Weather 13 (11): 807–819. [CrossRef] [Google Scholar]
- Olmedo O, Zhang J, Wechsler H, Poland A, Borne K. 2008. Automatic detection and tracking of coronal mass ejections in coronagraph time series. Sol Phys 248 (2): 485–499. [Google Scholar]
- Paassilta M, Raukunen O, Vainio R, Valtonen E, Papaioannou A, et al. 2017. Catalogue of 55–80 MeV solar proton events extending through solar cycles 23 and 24. J Space Weather Space Clim 7: A14. [CrossRef] [Google Scholar]
- Papaioannou A, Anastasiadis A, Sandberg I, Georgoulis MK, Tsiropoula G, Tziotziou K, Jiggens P, Hilgers A. 2015. A novel forecasting system for Solar Particle Events and Flares (FORSPEF). J Phys Conf Ser 632 (1): 012075, http://stacks.iop.org/1742-6596/632/i=1/a=012075. [Google Scholar]
- Papaioannou A, Sandberg I, Anastasiadis A, Kouloumvakos A, Georgoulis MK, Tziotziou K, Tsiropoula G, Jiggens P, Hilgers A. 2016. Solar flares, coronal mass ejections and solar energetic particle event characteristics. J Space Weather Space Clim 6: A42. [CrossRef] [EDP Sciences] [Google Scholar]
- Park J, Moon Y-J, Gopalswamy N. 2012. Dependence of solar proton events on their associated activities: Coronal mass ejection parameters. J Geophys Res: Space Phys 117(A8): 1–7. [Google Scholar]
- Parker E. 1965. Dynamical theory of the solar wind. Space Sci Rev 4 (5–6): 666–708. [CrossRef] [Google Scholar]
- Posner A. 2007. Up to 1-hour forecasting of radiation hazards from solar energetic ion events with relativistic electrons. Space Weather 5 (5): 1–28. [Google Scholar]
- Reames D, Barbier L, Ng C. 1996. The spatial distribution of particles accelerated by coronal mass ejection-driven shocks. ApJ 466: 473. [NASA ADS] [CrossRef] [Google Scholar]
- Reames DV. 1999. Particle acceleration at the Sun and in the heliosphere. Space Sci Rev 90 (3–4): 413–491. [NASA ADS] [CrossRef] [Google Scholar]
- Reames DV. 2015. What are the sources of solar energetic particles? Element abundances and source plasma temperatures. Space Sci Rev 194 (1–4): 303–327. [NASA ADS] [CrossRef] [Google Scholar]
- Richardson IG, von Rosenvinge TT, Cane HV. 2016. 25 MeV solar proton events in Cycle 24 and previous cycles. Adv Space Res, 60: 755–767. [CrossRef] [Google Scholar]
- Robbrecht E, Berghmans D. 2004. Automated recognition of coronal mass ejections (CMEs) in near-realtime data. A&A 425 (3): 1097–1106. [NASA ADS] [CrossRef] [EDP Sciences] [Google Scholar]
- Rodriguez J, Krosschell J, Green J. 2014. Intercalibration of GOES 8–15 solar proton detectors. Space Weather 12 (1): 92–109. [CrossRef] [Google Scholar]
- Rouillard A, Sheeley N, Tylka A, Vourlidas A, Ng C, et al. 2012. The longitudinal properties of a solar energetic particle event investigated using modern solar imaging. ApJ 752 (1): 44. [NASA ADS] [CrossRef] [Google Scholar]
- Smart D, Shea M. 1989. PPS-87: a new event oriented solar proton prediction model. Adv Space Res 9 (10): 281–284. [CrossRef] [EDP Sciences] [Google Scholar]
- Souvatzoglou G, Papaioannou A, Mavromichalaki H, Dimitroulakos J, Sarlanis C. 2014. Optimizing the real-time ground level enhancement alert system based on neutron monitor measurements: Introducing GLE Alert Plus. Space Weather 12 (11): 633–649. [CrossRef] [Google Scholar]
- St Cyr O, Posner A, Burkepile J. 2017. Solar energetic particle warnings from a coronagraph. Space Weather 15 (1): 240–257. [CrossRef] [Google Scholar]
- Strauss R, Fichtner H. 2015. On aspects pertaining to the perpendicular diffusion of solar energetic particles. ApJ 801 (1): 29. [Google Scholar]
- Tylka A, Cohen C, Dietrich W, Lee M, Maclennan C, Mewaldt R, Ng C, Reames D. 2005. Shock geometry, seed populations, and the origin of variable elemental composition at high energies in large gradual solar particle events. ApJ 625 (1): 474. [NASA ADS] [CrossRef] [Google Scholar]
- Tylka AJ, Lee MA. 2006. A model for spectral and compositional variability at high energies in large, gradual solar particle events. ApJ 646 (2): 1319. [NASA ADS] [CrossRef] [Google Scholar]
- Vainio R, Raukunen O, Tylka AJ, Dietrich WF, Afanasiev A. 2017. Why is solar cycle 24 an inefficient producer of high-energy particle events? A&A 604: A47. [Google Scholar]
- Wang Y, Chen C, Gui B, Shen C, Ye P, Wang S. 2011. Statistical study of coronal mass ejection source locations: Understanding CMEs viewed in coronagraphs. J Geophys Res A: Space Phys 116(A4): 1–15. [Google Scholar]
- Zhang M, Qin G, Rassoul H. 2009. Propagation of solar energetic particles in three-dimensional interplanetary magnetic fields. ApJ 692 (1): 109. [Google Scholar]
Cite this article as: Papaioannou A, Anastasiadis A, Sandberg I & Jiggens P 2018. Nowcasting of Solar Energetic Particle Events using near real-time Coronal Mass Ejection characteristics in the framework of the FORSPEF tool. J. Space Weather Space Clim. 8, A37.
All Tables
Solar energetic particle events occurrence probability depending on three CME speed ranges and three angular width ranges of CMEs, as obtained by Equation (1). The values within the brackets denote the error calculated from Equation (2). The values within the parenthesis correspond to 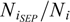 per i bin.
per i bin.
Linear regressions for the logarithm of the SEP Proton Peak Flux per CME width type and integral energy channel. Pearson’s correlation coefficients (cc), as well as their standard error SE cc are also presented, where n is the number of pairs used for the calculation of cc.
Summary of the categorical scores (POD, FAR) for higher energies, per pt. A corresponds to Hits, B to false positives, C to misses and D to true negatives.
All Figures
 |
Fig. 1. The derived SEP occurrence probabilities for all nine subgroups and the obtained fits per angular width of the CME. The blue line corresponds to Halo CMEs (AW = 360°), the red line to Partial Halo CMEs (120° ≤ AW ≤ 359°) and the green line corresponds to non halo CMEs (AW < 120°). The best fits are presented in Table 2. The error bars are calculated as: |
| In the text | |
 |
Fig. 2. Linear regressions between the CME speed and the logarithm of the SEP proton peak flux at several integral energy channels. The first column (stack of four plots) provides the regressions for the Halo CMEs (blue color). The second column shows the regressions for the Partial halo CMEs (red color) and the third column includes the regressions for the non halo CMEs (green color). For each column, from top to bottom the corresponding integral energy channels are E > 10 MeV, E > 30 MeV, E > 60 MeV and E > 100 MeV |
| In the text | |
 |
Fig. 3. Linear regressions between the CME speed and the logarithm of the SEP fluence at several integral energy channels. Similar to Figure 2. |
| In the text | |
 |
Fig. 4. A block diagram of the operational set up of FORSPEF’s sub-module based on CACTus near real-time CME identifications. |
| In the text | |
 |
Fig. 5. Categorical performance statistics for the FORSPEF CME module as a function of probability thresholds for E > 10 MeV covering 2013–2015. |
| In the text | |
 |
Fig. 6. An indicative example of the categorical performance statistics for the CME module as a function of probability thresholds (panel on the left) and the obtained POD and FAR for all 10 different trials, depicted as circles (panel on the right). The obtained POD and FAR from the initial sample (see Sect. 5.1.1 and Figure 5) are also marked in this latter panel as triangles, for comparison. |
| In the text | |
 |
Fig. 7. Comparison of the observed with the predicted peak proton flux for the SEP events listed in Table 5. Each plot corresponds to a specific provided energy and includes the number of SEP events that reach this energy; see text for details. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.